05.9 Ejercicio de entrenamiento de una red usando la infraestructura ResNet-50 que incorpora convoluciones (Información Complementaria)¶
Se presenta un ejercicio para ver como volcar los datos de imagenes sobre la red de convolución ResNet-50 y hacer una entrenamiento. Es una mera prueba de concepto por no disponerse de suficientes ejemplos para hacer un entrenamiento adecuado.
Se observará un sobreajuste en el conjunto de entrenamiento, mientras que en el conjunto de pruebas no se obtiene una buena exactitud.
El resultado es lógico por usar un conjunto de datos en número insuficiente
ResNet-50
https://pytorch.org/hub/pytorch_vision_resnet/
https://www.aprendemachinelearning.com/como-funcionan-las-convolutional-neural-networks-vision-por-ordenador/
Cursillo https://atcold.github.io/pytorch-Deep-Learning/es/week01/01-1/
En el problema de MNIST, las imágenes son de 28x28; por lo que una sola neurona plenamente conectado en una primera capa oculta de una red neuronal ordinaria tendría 28 x 28 = 784 pesos. Esta cantidad todavía parece manejable, pero es evidente que esta estructura totalmente conectado no funciona bien con imágenes más grandes.
Las redes neuronales convolucionales modelan de forma consecutiva pequeñas piezas de información, combinando esta información en las capas más profundas de la red. La primera capa intentará detectar los bordes y establecer patrones de detección de bordes. Luego, las capas posteriores trataran de combinarlos en formas más simples y, finalmente, en patrones de las diferentes posiciones de los objetos, iluminación, escalas, etc. Las capas finales intentarán hacer coincidir una imagen de entrada con todas los patrones y llegar a una predicción final como una suma ponderada de todos ellos, usando ya una red densa.
Las redes neuronales constan de 3 tipos de capas:
Convolucional, que es la que le da le nombre a la red.
De reducción o de pooling, la cual va a reducir la cantidad de parámetros al quedarse con las características más comunes.
Clasificadora, capa densa totalmente conectada, que da el resultado final de la red.
La imagen de entrada puede ser una matriz \(n \times m\) de enteros que representan el nivel de gris o una triple matriz de enteros representando los canales rojo, verde y azul en el caso de imagen de color. La matriz dará lugar a \(n \times m\) neuronas de entradas, simple o triple.
La operación de convolución se aplica sobre la imagen de entrada recibe como entrada o input la imagen y luego aplica sobre ella un filtro o kernel que nos devuelve un mapa de las características de la imagen original.
La capa de reducción o pooling se coloca generalmente después de la capa convolucional. Reduce las dimensiones espaciales (ancho x alto) del volumen de entrada para la siguiente capa convolucional. No afecta a la dimensión de profundidad del volumen. La operación que se suele utilizar en esta capa es max-pooling, que divide a la imagen de entrada en un conjunto de rectángulos y, respecto de cada subregión, se va quedando con el máximo valor.
Al final de las capas convolucional y de pooling, la capa clasificadora serán capas completamente conectadas en la que cada pixel se considera como una neurona separada. Y en salida habrá tantas neuronas como clases se deban predecir.
import glob, os
import numpy as np
from PIL import Image
from IPython import display
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torchvision import transforms
import torch
import torch.nn as nn
labels_animals = ["perro", "gato", "caballo", "vaca"]
def getLabelFileName(fileName):
for k in range(np.size(labels_animals)):
if (fileName.find(labels_animals[k])>-1):
return k
return -1
def importImagesFromPath(my_directory):
transform = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(256),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
#print(my_directory)
#os.chdir(my_directory)
imag_animal, label_animal = [],[]
#print(my_directory+"*.jpg")
for file in glob.glob(my_directory+"/*.jpg"):
#print(file)
label_animal.append(getLabelFileName(file))
PILimag = Image.open(file)
TensorImag = transform(PILimag)
BatchImag = TensorImag.unsqueeze(0) # create a mini-batch as expected by the model
imag_animal.append(BatchImag)
return imag_animal, torch.nn.functional.one_hot(torch.as_tensor(label_animal))
def getTensorImag(TenImag, IColor):
lstX=[]
lstY=[]
lstRGB=[]
Nx=TenImag.shape[2]
Ny=TenImag.shape[3]
minR, maxR = float(torch.min(TenImag[0][IColor[0]])), float(torch.max(TenImag[0][IColor[0]]))
minG, maxG = float(torch.min(TenImag[0][IColor[1]])), float(torch.max(TenImag[0][IColor[1]]))
minB, maxB = float(torch.min(TenImag[0][IColor[2]])), float(torch.max(TenImag[0][IColor[2]]))
#print(minR, maxR, minG, maxG, minB, maxB)
for iy in range(Ny):
for ix in range(Nx):
lstX.append(ix)
lstY.append(iy)
#lstRGB.append([0.5,0.5,0.5])
lstRGB.append([(float(TenImag[0][IColor[0]][Ny-iy-1][ix])-minR)/(maxR-minR), (float(TenImag[0][IColor[1]][Ny-iy-1][ix])-minG)/(maxG-minG), (float(TenImag[0][IColor[2]][Ny-iy-1][ix])-minB)/(maxB-minB)])
return lstX, lstY, lstRGB
##
#os.chdir('c:/Users/valer_z/Proyectos Python/Ejemplos Plaza Contratado Doctor/Cuadernos clase AA')
#print(os.getcwd())
imagAnimal_Train, targetAnimal_Train = importImagesFromPath("data/animalsTraining")
#os.chdir('c:/Users/valer_z/Proyectos Python/Ejemplos Plaza Contratado Doctor/Cuadernos clase AA')
#print(os.getcwd())
imagAnimal_Test, targetAnimal_Test = importImagesFromPath("./data/animalsTest")
print("done!", imagAnimal_Train[0].shape)
#os.chdir('c:/Users/valer_z/Proyectos Python/Ejemplos Plaza Contratado Doctor/Cuadernos clase AA')
done! torch.Size([1, 3, 256, 256])
Vemos el aspecto que tiene cada tensor de imagen cargado y sus convoluciones¶
T = imagAnimal_Train[4]
conv1 = nn.Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
conv2 = nn.Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
conv3 = nn.Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
TC1 = conv1(T)
TC2 = conv2(TC1)
TC3 = conv3(TC2)
lstX_1, lstY_1, lstRGB_1 = getTensorImag(T, [0,1,2])
lstX_2, lstY_2, lstRGB_2 = getTensorImag(TC1, [0,1,2])
lstX_3, lstY_3, lstRGB_3 = getTensorImag(TC2, [0,1,2])
lstX_4, lstY_4, lstRGB_4 = getTensorImag(TC3, [0,1,2])
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(35,10))
ax1.axis('off');ax2.axis('off');ax3.axis('off');ax4.axis('off')
ax1.scatter(lstX_1,lstY_1, c=lstRGB_1, s=20)
ax2.scatter(lstX_2,lstY_2, c=lstRGB_2, s=20)
ax3.scatter(lstX_3,lstY_3, c=lstRGB_3, s=20)
ax4.scatter(lstX_4,lstY_4, c=lstRGB_4, s=20)
fig.show()
<ipython-input-7-37d32fdc5b60>:18: UserWarning: Matplotlib is currently using module://ipykernel.pylab.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()

Definir la Red Arquitectura¶
Aquí, se definirá una arquitectura CNN. En lugar de un Perceptrón Multicapa, que usó capas lineales y completamente conectadas, se usará lo siguiente:
Convolutional layers, que se puede considerar como una pila de imágenes filtradas.
Maxpooling layers, que reducen el tamaño x-y de una entrada, manteniendo solo los píxeles más activos de la capa anterior.
Las capas habituales Linear + Dropout para evitar sobreajuste y producir una salida de dimensión 10.
El resultado es una red con 2 capas convolucionales que se muestra en la imagen a continuación y en el código, y se le ha dado un código de inicio con una capa convolucional y una capa máxima.
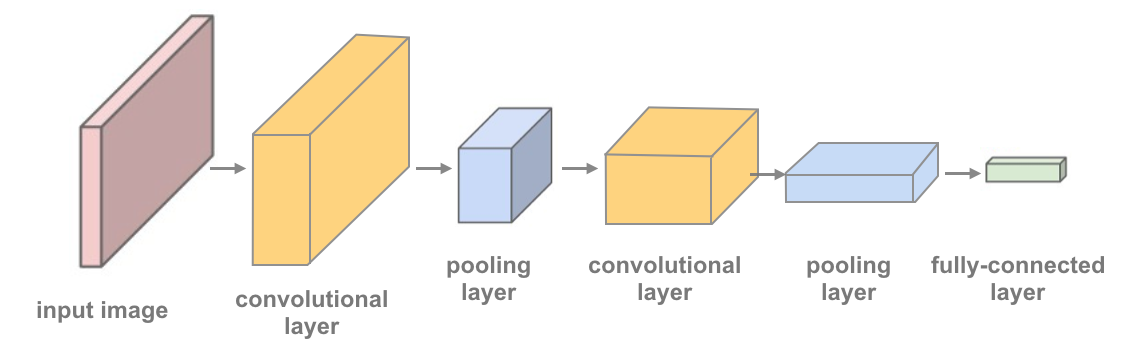
Definir un modelo con múltiples capas convolucionales y definir el comportamiento de la red de avance.¶
Cuantas más capas convolucionales se incluyan, más patrones complejos de color y forma podrá detectar un modelo. Se sugiere que el modelo final incluya 2 o 3 capas convolucionales, así como capas lineales + dropout en el medio para evitar el sobreajuste.
Es una buena práctica observar las investigaciones e implementaciones existentes de modelos relacionados como punto de partida para definir sus propios modelos. Puede resultarle útil mirar este ejemplo de clasificación de PyTorch o este, un ejemplo más complejo de Keras para ayudar a decidir la estructura final.
Volumen de salida para una capa convolucional¶
Para calcular el tamaño de salida de una capa convolucional dada, podemos realizar el siguiente cálculo (tomado del [curso cs231n de Stanford] (http://cs231n.github.io/convolutional-networks/#layers)):
Podemos calcular el tamaño espacial del volumen de salida en función del tamaño del volumen de entrada (W), el tamaño del núcleo / filtro (F), la zancada con la que se aplican (S) y la cantidad de relleno de ceros utilizado (P) en la frontera. La fórmula correcta para calcular cuántas neuronas definen el output_W viene dada por
(W − F + 2P) / S + 1.
Por ejemplo, para una entrada de 7x7 y un filtro de 3x3 con stride 1 y pad 0 obtendríamos una salida de 5x5. Con la zancada 2 obtendríamos una salida de 3x3.
# define the CNN architecture
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# convolutional layer (sees 32x32x3 image tensor)
self.conv1 = nn.Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
# convolutional layer (sees 16x16x16 tensor)
self.conv2 = nn.Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
# convolutional layer (sees 8x8x32 tensor)
self.conv3 = nn.Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
# max pooling layer
self.pool = nn.MaxPool2d(2, 2)
# linear layer (64 * 4 * 4 -> 500)
self.fc1 = nn.Linear(64 * 4 * 4, 500)
# linear layer (500 -> 10)
self.fc2 = nn.Linear(500, 10)
# dropout layer (p=0.25)
self.dropout = nn.Dropout(0.25)
def forward(self, x):
# add sequence of convolutional and max pooling layers
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = self.pool(F.relu(self.conv3(x)))
# flatten image input
x = x.view(-1, 64 * 4 * 4)
# add dropout layer
x = self.dropout(x)
# add 1st hidden layer, with relu activation function
x = F.relu(self.fc1(x))
# add dropout layer
x = self.dropout(x)
# add 2nd hidden layer, with relu activation function
x = self.fc2(x)
return x
# create a complete CNN
model = Net()
print(model)
## move tensors to GPU if CUDA is available
#if torch.cuda.is_available():
# model.cuda()
Net(
(conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(conv2): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(conv3): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=500, bias=True)
(fc2): Linear(in_features=500, out_features=10, bias=True)
(dropout): Dropout(p=0.25, inplace=False)
)
Especificar la [Función de pérdida] (http://pytorch.org/docs/stable/nn.html#loss-functions) y el [Optimizador] (http://pytorch.org/docs/stable/optim.html)¶
Decidir qué función de optimización y pérdida es la más adecuada para esta tarea de clasificación. Los ejemplos de códigos vinculados de arriba pueden ser un buen punto de partida; [este ejemplo de clasificación de PyTorch] (https://github.com/pytorch/tutorials/blob/master/beginner_source/blitz/cifar10_tutorial.py) o [este, un ejemplo más complejo de Keras] (https://github.com/keras -equipo / keras / blob / master / examples / cifar10_cnn.py). Prestar mucha atención al valor de ** tasa de aprendizaje **, ya que este valor determina cómo el modelo converge a un pequeño error.
import torch.optim as optim
# specify loss function (categorical cross-entropy)
criterion = nn.CrossEntropyLoss()
# specify optimizer
optimizer = optim.SGD(model.parameters(), lr=0.01)
Entrenamiento de la red¶
Hay que observar como la pérdida en entrenamiento y validación disminuye con el tiempo; si la pérdida de validación aumenta alguna vez, indica un posible sobreajuste.
# number of epochs to train the model
n_epochs = 50
valid_loss_min = np.Inf # track change in validation loss
for epoch in range(1, n_epochs+1):
# keep track of training and validation loss
train_loss = 0.0
valid_loss = 0.0
###################
# train the model #
###################
model.train()
##for data, target in train_loader:
for K in range(targetAnimal_Train.size(0)):
imagAnimal = imagAnimal_Train[K]
targetAnimal = targetAnimal_Train[K]
## move tensors to GPU if CUDA is available
#if torch.cuda.is_available():
# imagAnimal, targetAnimal = imagAnimal.cuda(), targetAnimal.cuda()
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(imagAnimal)
# calculate the batch loss
loss = criterion(output, targetAnimal)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update training loss
train_loss += loss.item()*targetAnimal_Train.size(0)
######################
# validate the model #
######################
model.eval()
#for data, target in valid_loader:
for K in range(targetAnimal_Test.size(0)):
imagAnimal = imagAnimal_Test[K]
targetAnimal = targetAnimal_Test[K]
## move tensors to GPU if CUDA is available
#if torch.cuda.is_available():
# imagAnimal, targetAnimal = imagAnimal.cuda(), targetAnimal.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(imagAnimal)
# calculate the batch loss
loss = criterion(output, targetAnimal)
# update average validation loss
valid_loss += loss.item()*targetAnimal_Test.size(0)
# calculate average losses
train_loss = train_loss/targetAnimal_Train.size(0)
valid_loss = valid_loss/targetAnimal_Test.size(0)
# print training/validation statistics
print('Epoch: {} \tTraining Loss: {:.6f} \tValidation Loss: {:.6f}'.format(
epoch, train_loss, valid_loss))
# save model if validation loss has decreased
if valid_loss <= valid_loss_min:
print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model ...'.format(
valid_loss_min,
valid_loss))
torch.save(model.state_dict(), 'data/model_animals.pt')
valid_loss_min = valid_loss
torch.save(model.state_dict(), 'data/model_end.pt')
Epoch: 1 Training Loss: 83.792263 Validation Loss: 28.138700
Validation loss decreased (inf --> 28.138700). Saving model ...
Epoch: 2 Training Loss: 39.992820 Validation Loss: 9.804148
Validation loss decreased (28.138700 --> 9.804148). Saving model ...
Epoch: 3 Training Loss: 23.158674 Validation Loss: 9.118185
Validation loss decreased (9.804148 --> 9.118185). Saving model ...
Epoch: 4 Training Loss: 23.352449 Validation Loss: 8.881914
Validation loss decreased (9.118185 --> 8.881914). Saving model ...
Epoch: 5 Training Loss: 23.066660 Validation Loss: 8.754663
Validation loss decreased (8.881914 --> 8.754663). Saving model ...
Epoch: 6 Training Loss: 22.590097 Validation Loss: 8.855216
Epoch: 7 Training Loss: 22.091288 Validation Loss: 8.361208
Validation loss decreased (8.754663 --> 8.361208). Saving model ...
Epoch: 8 Training Loss: 20.447096 Validation Loss: 8.217079
Validation loss decreased (8.361208 --> 8.217079). Saving model ...
Epoch: 9 Training Loss: 19.415829 Validation Loss: 8.139205
Validation loss decreased (8.217079 --> 8.139205). Saving model ...
Epoch: 10 Training Loss: 19.278581 Validation Loss: 8.295506
Epoch: 11 Training Loss: 18.145964 Validation Loss: 7.793819
Validation loss decreased (8.139205 --> 7.793819). Saving model ...
Epoch: 12 Training Loss: 16.406845 Validation Loss: 7.476499
Validation loss decreased (7.793819 --> 7.476499). Saving model ...
Epoch: 13 Training Loss: 16.918698 Validation Loss: 7.849444
Epoch: 14 Training Loss: 15.405316 Validation Loss: 7.742910
Epoch: 15 Training Loss: 13.469188 Validation Loss: 7.678387
Epoch: 16 Training Loss: 11.710447 Validation Loss: 8.086330
Epoch: 17 Training Loss: 11.698695 Validation Loss: 8.259715
Epoch: 18 Training Loss: 9.961738 Validation Loss: 8.589515
Epoch: 19 Training Loss: 7.327819 Validation Loss: 9.232945
Epoch: 20 Training Loss: 10.917610 Validation Loss: 9.671700
Epoch: 21 Training Loss: 6.659675 Validation Loss: 10.018299
Epoch: 22 Training Loss: 8.422542 Validation Loss: 10.824869
Epoch: 23 Training Loss: 4.800786 Validation Loss: 10.324398
Epoch: 24 Training Loss: 5.150071 Validation Loss: 10.876208
Epoch: 25 Training Loss: 4.856150 Validation Loss: 12.738497
Epoch: 26 Training Loss: 2.938190 Validation Loss: 11.686457
Epoch: 27 Training Loss: 1.624716 Validation Loss: 13.694622
Epoch: 28 Training Loss: 1.059613 Validation Loss: 13.363434
Epoch: 29 Training Loss: 5.309131 Validation Loss: 14.380370
Epoch: 30 Training Loss: 4.510987 Validation Loss: 14.544600
Epoch: 31 Training Loss: 3.924983 Validation Loss: 15.504646
Epoch: 32 Training Loss: 6.777555 Validation Loss: 13.994958
Epoch: 33 Training Loss: 2.040812 Validation Loss: 16.786807
Epoch: 34 Training Loss: 2.215244 Validation Loss: 14.155369
Epoch: 35 Training Loss: 1.407099 Validation Loss: 14.777567
Epoch: 36 Training Loss: 2.614070 Validation Loss: 16.547811
Epoch: 37 Training Loss: 4.159538 Validation Loss: 21.027229
Epoch: 38 Training Loss: 0.924696 Validation Loss: 19.147886
Epoch: 39 Training Loss: 0.723268 Validation Loss: 18.259392
Epoch: 40 Training Loss: 0.989082 Validation Loss: 20.137300
Epoch: 41 Training Loss: 1.056692 Validation Loss: 18.489841
Epoch: 42 Training Loss: 1.755392 Validation Loss: 19.284278
Epoch: 43 Training Loss: 0.491398 Validation Loss: 21.164300
Epoch: 44 Training Loss: 0.824325 Validation Loss: 19.761147
Epoch: 45 Training Loss: 1.512708 Validation Loss: 20.583673
Epoch: 46 Training Loss: 3.903600 Validation Loss: 22.546982
Epoch: 47 Training Loss: 2.489610 Validation Loss: 20.426097
Epoch: 48 Training Loss: 8.976113 Validation Loss: 16.649943
Epoch: 49 Training Loss: 2.135595 Validation Loss: 16.313875
Epoch: 50 Training Loss: 1.111219 Validation Loss: 17.395826
print(imagAnimal_Test[5].shape, targetAnimal_Test[5])
torch.Size([1, 3, 256, 256]) tensor([0, 0, 0, 1])
modelOk = Net()
modelOk.load_state_dict(torch.load('data/model_end.pt'))
modelOk.eval()
Net(
(conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(conv2): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(conv3): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=500, bias=True)
(fc2): Linear(in_features=500, out_features=10, bias=True)
(dropout): Dropout(p=0.25, inplace=False)
)
Ahora chequeamos algún elemento del conjunto de validación¶
# Oks = 3;5;12;14
Itest = 14
#Out_Test = modelOk.forward(imagAnimal_Train[Itest])
Out_Test = modelOk(imagAnimal_Test[Itest])
pred = Out_Test.max(1, keepdim=True)
print("pred=", pred)
#print("Predict", torch.max(Out_Test,1))
#print(Out_Test)
#print(torch.nn.functional.softmax(Out_Test[0], dim=0))
print(targetAnimal_Test[Itest])
print(Out_Test)
pred= torch.return_types.max(
values=tensor([[13.0471],
[ 9.5229],
[12.5875],
[12.4432]], grad_fn=<MaxBackward0>),
indices=tensor([[0],
[0],
[1],
[0]]))
tensor([0, 0, 1, 0])
tensor([[13.0471, 1.1603, -1.5832, -1.5864, -1.5719, -1.6322, -2.2044, -2.1717,
-2.3683, -1.8164],
[ 9.5229, 2.0306, -1.0871, -1.4103, -1.4309, -1.8840, -1.6909, -1.6318,
-1.7163, -1.1122],
[ 1.8139, 12.5875, -1.7377, -1.7615, -2.3746, -1.9114, -2.2021, -1.9775,
-1.9069, -1.6795],
[12.4432, 1.7451, -1.2855, -0.9964, -1.1740, -1.8617, -1.7974, -2.4439,
-1.7314, -1.2914]], grad_fn=<AddmmBackward0>)
T = imagAnimal_Test[Itest]
lstX, lstY, lstRGB = getTensorImag(T, [0,1,2])
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(35,15))
plt.rc('font', size=24)
ax1.scatter(lstX,lstY, c=lstRGB, s=20)
ax1.axis('off')
ax2.barh(np.arange(4), pred[1])
ax2.set_aspect(0.1)
ax2.set_yticks(np.arange(4))
ax2.set_yticklabels(['perro','gato','caballo','vaca'], size='small');
ax2.set_title('Probabilidad')
ax2.set_xlim(0, 1.1)
fig.show()
plt.tight_layout()
/home/carlos/.local/lib/python3.8/site-packages/numpy/lib/stride_tricks.py:536: FutureWarning: The input object of type 'Tensor' is an array-like implementing one of the corresponding protocols (`__array__`, `__array_interface__` or `__array_struct__`); but not a sequence (or 0-D). In the future, this object will be coerced as if it was first converted using `np.array(obj)`. To retain the old behaviour, you have to either modify the type 'Tensor', or assign to an empty array created with `np.empty(correct_shape, dtype=object)`.
args = [np.array(_m, copy=False, subok=subok) for _m in args]
/home/carlos/.local/lib/python3.8/site-packages/numpy/lib/stride_tricks.py:536: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.
args = [np.array(_m, copy=False, subok=subok) for _m in args]
/home/carlos/.local/lib/python3.8/site-packages/numpy/core/_asarray.py:102: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.
return array(a, dtype, copy=False, order=order)
<ipython-input-14-afde7516c190>:13: UserWarning: Matplotlib is currently using module://ipykernel.pylab.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()

