.ipynb .pdf

Contents

02.1 Clasificación naive-Bayes

Ejemplos del empleo de los clasificadores

Un clasificador es un método supervisado que permite entrenar un modelo para que determine la clase más probable que debemos asignar a un registro dado de características. Para ello el conjunto de entrenamiento tendrá una serie de \(N\) registros clasificados, que permiten al ordenador aprender a clasificar registros sin clase. Por ejemplo:

• Detección de SPAM. En base a un conjunto de características de los correos se entrena con supervisión al ordenador para que determine si son o no SPAM.

• Datos de microarrays. A partir de un subconjunto de genes óptimos para diagnosticar cancer.

Detalle del método Naïve Bayes

Probabilidad de clasificar un vector de atributos en una clase

Sabiendo que un registro de nuestro conjunto tiene \(x\) como vector de atributos, ¿cuál es la probabilidad de clasificarla en la clase \(c\)? Ello requiere estimar:

\[P(c|x)=\frac{P(c \cap x)}{P(x)}\]

Es difícil utilizar frecuencias para resolver esta probabilidad, pues se necesitarian muchos registros en el conjunto de entrenamiento con exactamente el mismo vector \(x\) de atrubutos. Por ellos se recurre al teorema de Bayes sobre probabilidad condicionada

\[P(c \cap x)=P(x|c)P(c)\]

Por lo tanto

\[P(c|x)=\frac{P(x|c)P(c)}{P(x)}\]

• P(x|c) se denomina verosimilitud (likelihood).

• P(c|x) se llama probabilidad a posteriori de la clase (posterior).

• P(c) se llama probabilidad a priori de la clase.

• P(x) se llama verosimilitud marginal (o probabilidad a priori del vector de atributos).

Se tomará aquella clase cuya probabilidad a posteriori es mayor

• Es decir, aquella clase \(c\) cuya \(P(c|x)\) sea máxima:

\[ clase(x) = \underset{c \in \{1,...,m\}}{\arg\max} P(c|x) = \underset{c \in \{1,...,m\}}{\arg\max} \frac{P(x|c)P(c)}{P(x)} \]

• Y como \(P(x)\) no depende de \(c\) bastará con tomar el valor máximo de:

\[ clase(x) = \underset{c \in \{1,...,m\}}{\arg\max} P(x|c)P(c)\]

Suposición Naïf

• Los atributos observados en cualquier instancia son independientes una vez que sabemos que la instancia pertenece a la clase \(c\). Esto es si el vector \(x\) está formado por \(n\) atributos (\(x=(x_1, x_2, ..., x_n)\)). La probabilidad \(P(x|c)\) es:

\[P(x|c) = P(x_1|c)P(x_2|c) \cdots P(x_n|c)=\prod\limits_{i=1}^{n}P(x_i|c)\]

Estimación de probabilidades

Estimar \(P(c)\) es tan sencillo como calcular la frecuencia de la clase en el conjunto de entrenamiento:

\[P(c)=\frac{n_c}{N}\]

Siendo \(n_c\) el número de registros de clase \(c\) en el conjunto de entrenamiento. Y \(N\) el total de elementos en el conjunto de entrenamiento.

Estimar la verosimilitud \(P(x_i|c)\) depende de:

• Si los atributos \(x_i\) son discretos (caso DNA splicing) se cuentan las frecuencias.

• Si los atributos \(x_i\) son continuos (caso conjunto Iris) se supone que cada atributo se distribuye de acuerdo a una normal

\[ x_i|c\sim N(\mu_i^c, (\sigma_i^c)^2) \]

y se utiliza la función de densidad gaussiana:

\[ P(x_i|c)=\phi(x_i;\mu_i^c,(\sigma_i^c)^2)=\frac{1}{\sqrt{2\pi}\sigma_i^c}exp\left(-\frac{(x_i-\mu_i^c)^2}{2(\sigma_i^c)^2}\right) \]

Características de la clasificación Naïve-Bayes

Ventajas:

• Simple, rápido y efectivo.

• Da buenos resultados con datos con ruido.

• Requiere relativamente pocos registros para entrenar, y también funciona bien con grandes conjuntos de datos.

• Proporciona fácilmente la probabilidad estimada para cada predicción.

Inconvenientes:

• Supone independencia entre atributos, lo cual normalmente es falso.

• En general no funciona bien con atributos numéricos, sobre todos si hay muchos.

• La clasicación predicha es más creíble que las probabilidades estimadas. Esto es debemos confiar más en el resultado \(c\) obtenido en que en el valor numérico \(P(c|x)\) como probabalidad.

Aplicar el método Naïve-Bayes para clasificar el conjunto Iris

El conjunto de datos de Iris se encuentra en la librería sk-learn, por lo que se importa de ahí

• Primero se vuelca a un DataFrame, con 4 columnas con sus caracteristicas y una columna con la clasificación objetivo

• Se muestra la descripción de cada uno de los valores (0, 1, 2) objetivo.

from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target']=iris['target']
df.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0

iris['target_names']

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

Inicialmente se divide el conjunto de datos de entrada en Entrenamiento (75%) y Validación (25%). Conjuntos Train y Test

• Para hacer esta división del conjunto se utiliza una función de la librería sk-learn: train_test_split

• Los parámetro train_test o test_size : indica el ratio que tiene el conjunto de entrenamiento o validación respecto al total.

• El parámetro shuffle : indica si los datos se barajan antes de dividirse

• El parámetro random_state : se indica que la división aleatoria ha de ser reproducible

• El parámetro stratity : indica que la división se realiza proporcional a los valores de las etiquetas

Mas detalles : https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html

from sklearn.model_selection import train_test_split
X, y = df.values[:,0:4], df.values[:,4]
X_train, X_test, y_train, y_test =train_test_split(X, y, test_size=0.25, random_state=0, stratify=y)

y_test

array([0., 0., 0., 0., 1., 1., 1., 0., 1., 2., 2., 2., 1., 2., 1., 0., 0.,
       2., 0., 1., 2., 1., 1., 0., 2., 0., 0., 1., 2., 1., 0., 1., 2., 2.,
       0., 1., 2., 2.])

Implementación directa de la fórmula Naive Bayes

Cálculo de las Medias por clase y característica

### Vector de Medias
import numpy as np
numClases = np.size(np.unique(df['target']))
mean_vectors = []
for cl in range(numClases):
    mean_vectors.append(np.mean(X_train[y_train==cl], axis=0))
    print('Vector Media clase %s: %s\n' %(cl, mean_vectors[cl]))

Vector Media clase 0: [5.00540541 3.42432432 1.44324324 0.24864865]

Vector Media clase 1: [5.8972973  2.72702703 4.23513514 1.32432432]

Vector Media clase 2: [6.67368421 2.96842105 5.58421053 2.03421053]

cols = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
w_df = pd.DataFrame(mean_vectors, columns=cols)
w_df.insert(0, 'Variedad', iris['target_names'])
w_df.head()

	Variedad	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	setosa	5.005405	3.424324	1.443243	0.248649
1	versicolor	5.897297	2.727027	4.235135	1.324324
2	virginica	6.673684	2.968421	5.584211	2.034211

Cálculo de las Desviaciones Típicas por clase y característica

### Vector de Desviaciones Estándar
import numpy as np
numClases = np.size(np.unique(df['target']))
sds_vectors = []
for cl in range(numClases):
    sds_vectors.append(np.std(X_train[y_train==cl], axis=0))
    print('Desviación estándar clase %s: %s\n' %(cl, sds_vectors[cl]))

Desviación estándar clase 0: [0.37772144 0.40895741 0.17636041 0.1029868 ]

Desviación estándar clase 1: [0.50268817 0.30637254 0.51001654 0.20189026]

Desviación estándar clase 2: [0.63523067 0.32126826 0.58558397 0.25160152]

Nota:

La expresión y_train==cl devuelve una lista de true/false dependiendo de si se cumple la comparación.

El array/arreglo X_train[y_train==cl] es una copia de los datos de X_train cuando la condición es true

y_train==cl

array([False, False, False, False,  True,  True, False, False, False,
       False, False, False, False,  True, False, False, False, False,
       False,  True,  True, False, False,  True,  True,  True,  True,
       False, False,  True,  True,  True, False, False, False,  True,
        True, False, False,  True,  True, False, False, False, False,
       False,  True, False, False,  True, False,  True, False, False,
       False, False, False,  True, False, False, False, False,  True,
       False, False, False, False, False,  True, False,  True, False,
       False,  True,  True, False,  True, False, False, False, False,
        True, False,  True, False, False, False, False, False, False,
        True,  True,  True, False,  True, False,  True, False, False,
       False, False, False, False,  True,  True, False, False, False,
       False,  True,  True,  True])

cols = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
w_df = pd.DataFrame(sds_vectors, columns=cols)
w_df.insert(0, 'Variedad', iris['target_names'])
w_df.head()

	Variedad	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	setosa	0.377721	0.408957	0.176360	0.102987
1	versicolor	0.502688	0.306373	0.510017	0.201890
2	virginica	0.635231	0.321268	0.585584	0.251602

Cálculo de las probabilidades por clase

¡Es el porcentaje que tiene cada clase \((0, 1, ..., k-1)\) en el conjunto y_train, matriz columna con las clasificaciones del conjunto de entrenamiento!

### Vector de Probabilidades
numClases = np.size(np.unique(df['target']))
probab = []
for cl in range(numClases):
    probab.append(np.size(y_train[y_train==cl])/np.size(y_train))
    print('Probabilidad clase %s: %s\n' %(cl, probab[cl]))
np.sum(probab)

Probabilidad clase 0: 0.33035714285714285

Probabilidad clase 1: 0.33035714285714285

Probabilidad clase 2: 0.3392857142857143

1.0

cols = ['Probabilidad']
w_df = pd.DataFrame(probab, columns=cols)
w_df.insert(0, 'Variedad', iris['target_names'])
w_df.head()

	Variedad	Probabilidad
0	setosa	0.330357
1	versicolor	0.330357
2	virginica	0.339286

Implementamos una función para calcular la probabilidad de un observación por Naive-Bayes

norm.pdf implementa la función de densidad de una distribución normal de media \(\mu\) y desviación típica \(\sigma\):

\[f(x)=\frac{1}{\sigma\sqrt{2\pi}} \cdot e^\frac{(x-\mu)^2}{2\sigma^2}\]

Se calcula la probabilidad \(P(X_1|C) \cdot P(X_2|C)...P(X_p|C) \cdot P(C)\) de los p tipos observados \(x\) siendo C cada clase \((0, 1, ..., k-1)\). El cálculo se almacena en una estructura p de tipo dictionary. En lugar de un dictionary se podría haber optado por una lista o array también.

p va a contener k valores con la probabilidad de pertener a cada clase según los valores de sus caracteristicas observadas x.

En el proceso, primero se inicializa p con la probabilidad marginal de cada clase \(P(C)\), finalmente se le multiplica por la función de densidad de la normal de los p valores observados \(X_1\) … \(X_p\).

El resultado de la función es la clase de máxima probabilidad que coincide con la posición del mayor valor, pues pd.Series(p).values convierte el dictionary en un arreglo o vector donde la posiciones coinciden en este caso con las clases \((0, 1, ..., k-1)\). La posición de máximo valor lo da el método argmax()

from scipy.stats import norm
def NaiveBayes(x, mean_vectors, sds_vectors, probab, numClases):
    p={} ##Lista tipo dictionary con la probabilidad de pertener a cada clase de cada observacion x
    for cl in range(numClases):
        p[cl]=probab[cl]
        ## Para cada columna de datos
        for ix in range(np.size(x)):
            p[cl] *= norm.pdf(x[ix], mean_vectors[cl][ix], sds_vectors[cl][ix])
    print(x, pd.Series(p).values,pd.Series(p).values.argmax())
    return pd.Series(p).values.argmax()

Se llama a NaiveBayes y por cada observación \(x\) del conjunto de entrenamiento se calcula el valor estimado. La calidad del clasificador vendrá dada por la exactitud o porcentaje de aciertos entre estimados y reales.

Nota: zip es una función de Python que nos permite recorrer con for simultaneamente dos listas X_test e y_test.

numClases = np.size(np.unique(df['target']))
tot_Test = np.size(y_test)
tot_aciertos = 0
y_pred = []
for x, y in zip(X_test, y_test):
    y_est = NaiveBayes(x, mean_vectors, sds_vectors, probab, numClases)
    y_pred.append(y_est)
    if (y==y_est): tot_aciertos +=1
    #print('Instancia %s Clase real %s - Clase estimada %s \n' %(x, y, y_est))
print('Exactitud del clasificador (porcentaje de aciertos)= %s \n' %(tot_aciertos*100/tot_Test))

[5.1 3.4 1.5 0.2] [2.45053081e+00 1.40834091e-15 4.24516083e-25] 0
[4.8 3.  1.4 0.1] [5.14231359e-01 6.59754490e-17 4.41419094e-27] 0
[5.3 3.7 1.5 0.2] [1.48897676e+00 1.76221893e-16 1.62544089e-25] 0
[5.1 3.3 1.7 0.5] [4.86620446e-02 2.69964773e-11 1.83666064e-20] 0
[5.5 2.4 3.7 1. ] [4.22091386e-49 3.46640936e-02 1.31176675e-08] 1
[5.7 2.8 4.5 1.3] [2.34482501e-89 4.11993004e-01 1.96205104e-04] 1
[5.7 2.8 4.1 1.3] [2.11734622e-73 4.55207624e-01 4.38660082e-05] 1
[4.9 3.1 1.5 0.1] [7.01828920e-01 2.06514800e-16 2.13993825e-26] 0
[6.  3.4 4.5 1.6] [2.22155073e-104 1.59272776e-002 2.68454733e-003] 1
[7.2 3.  5.8 1.6] [1.00870839e-177 4.39076609e-005 4.25316843e-002] 2
[6.3 3.3 6.  2.5] [1.46923280e-251 7.23724703e-012 1.97671020e-002] 2
[5.6 2.8 4.9 2. ] [1.62120692e-147 6.80577785e-004 2.98949661e-002] 2
[5.8 2.7 4.1 1. ] [9.91518524e-63 1.37064865e-01 6.75755009e-07] 1
[6.3 2.9 5.6 1.8] [4.59079436e-173 5.66551107e-004 1.52330264e-001] 2
[5.5 2.5 4.  1.3] [5.30158203e-70 2.61933882e-01 6.52762843e-06] 1
[5.1 3.7 1.5 0.4] [7.42711731e-01 1.54601530e-14 1.87618653e-23] 0
[4.6 3.1 1.5 0.2] [1.03975908e+00 9.43308914e-16 1.00449689e-25] 0
[6.5 3.  5.2 2. ] [3.25040154e-165 1.06773481e-004 2.18916674e-001] 2
[5.1 3.8 1.5 0.3] [1.58947359e+00 4.76165116e-16 6.15106145e-25] 0
[6.4 3.2 4.5 1.5] [1.43282835e-100 5.81720409e-002 3.79875469e-003] 1
[5.9 3.  5.1 1.8] [2.47205624e-144 5.24951581e-003 6.24090377e-002] 2
[5.6 3.  4.1 1.3] [6.22746692e-73 2.85524982e-01 3.88625760e-05] 1
[6.7 3.1 4.7 1.5] [7.22470363e-111 3.17724489e-002 8.81619453e-003] 1
[5.1 3.5 1.4 0.2] [2.46619493e+00 2.23454911e-16 7.97369617e-26] 0
[6.1 2.6 5.6 1.4] [9.93809704e-151 1.15905672e-002 4.10714560e-003] 1
[5.5 3.5 1.3 0.2] [8.00083749e-01 1.89714964e-16 9.05270240e-26] 0
[4.8 3.4 1.9 0.2] [8.02814901e-02 2.25613080e-14 1.09419202e-23] 0
[5.5 2.6 4.4 1.2] [4.51348444e-81 2.78209223e-01 1.42576570e-05] 1
[5.8 2.7 5.1 1.9] [4.42283516e-151 2.10172494e-003 4.82491420e-002] 2
[6.7 3.1 4.4 1.4] [6.19408126e-93 6.21826012e-02 1.41753140e-03] 1
[5.1 3.8 1.6 0.2] [1.14214454e+00 9.58028320e-17 1.19074941e-25] 0
[6.5 2.8 4.6 1.5] [8.66406112e-106 1.32542449e-001 6.13548757e-003] 1
[6.9 3.1 5.4 2.1] [2.50829324e-185 1.57911395e-006 2.26872382e-001] 2
[5.7 2.5 5.  2. ] [3.26503513e-153 4.45766225e-004 1.83716171e-002] 2
[4.6 3.4 1.4 0.3] [1.43428769e+00 8.48053216e-16 2.22315713e-25] 0
[7.  3.2 4.7 1.4] [1.46132813e-107 8.89297426e-003 2.57720499e-003] 1
[6.3 3.4 5.6 2.4] [3.41814743e-218 6.54378179e-010 3.38810942e-002] 2
[7.2 3.6 6.1 2.5] [8.61336276e-263 1.71431432e-014 3.59021543e-003] 2
Exactitud del clasificador (porcentaje de aciertos)= 97.36842105263158 

Finalmente presentamos la matriz de confusión de la clasificación anterior

La matriz de confusión tiene tantas filas y columnas como clases. Las filas representan las clases correctas del conjunto de validación y las columnas las estimaciones realizadas. Si la precisión es 100% sale una matriz diagonal.

En este primer caso utilizamos un procedimiento poco encapsulado para obtener la matriz de confusión, dado que la clasificación se ha realizado con una rutina propia. A continuación, al usar un clasificador de sk-learn, será posible utilizar una función más encapsulada y con mejor salida gráfica para representar la matriz de confusión.

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
cm=confusion_matrix(y_test, y_pred)
classNames = iris['target_names']
numClass = np.size(classNames)
plt.clf()
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Wistia)
for i in range(numClass):
    for j in range(numClass):
        plt.text(j,i, str(cm[i][j]))

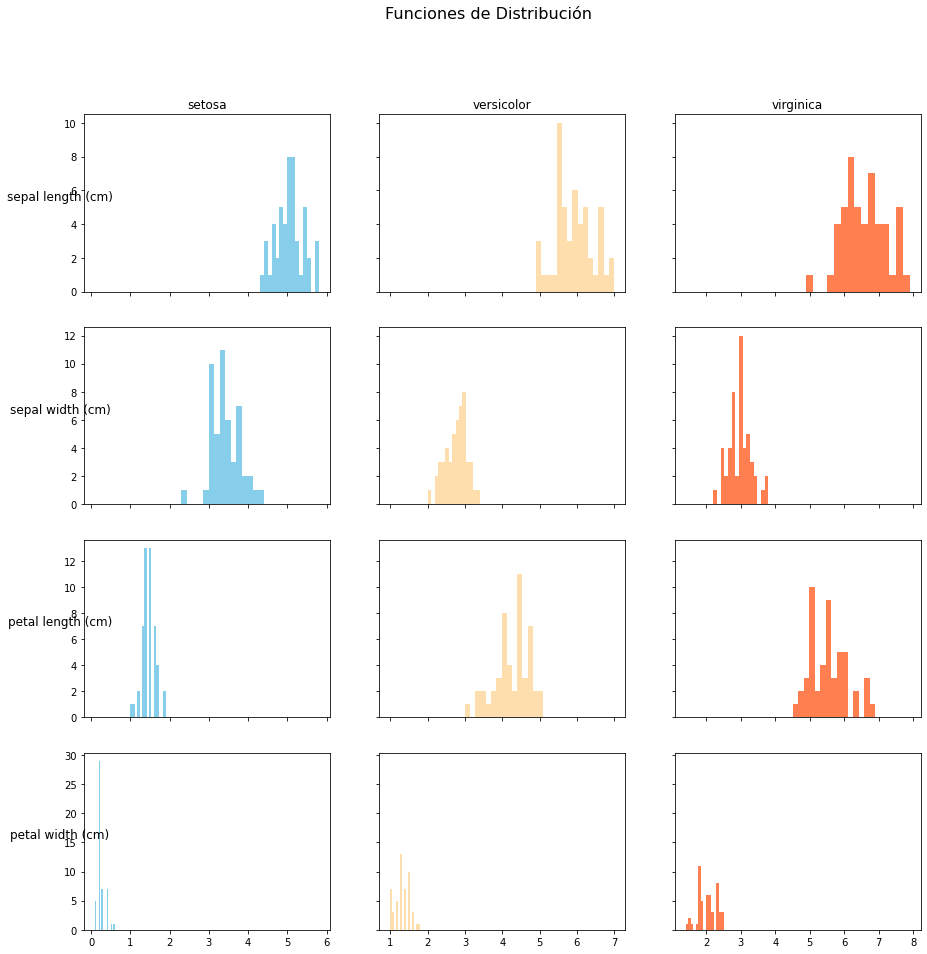
Se muestra en detalle la función de distribución de cada clase

Como se distribuyen en cada clase de Iris las distintos caracteristicas analizadas según sus valores.

Se emplea subplots(Filas, Columnas,[…]) que permite realizar dibujos multiples en filas, columnas o cuadriculas.

En cada dibujo se vuelca el histograma con el método hist sobre los valores de cada característica y clase considerada. Para más detalle:

https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.subplots.html

https://matplotlib.org/stable/gallery/subplots_axes_and_figures/subplots_demo.html

import matplotlib.pyplot as plt
cols = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
className = iris['target_names']
y=df['target']
fig, ax = plt.subplots(np.size(cols), np.size(className), sharex='col', sharey='row', figsize=(15,15))
fig.suptitle('Funciones de Distribución', fontsize=16)
colors=["skyblue", "navajowhite", "coral"]
for i in range(np.size(cols)):
    _x = df[cols[i]]
    for j in range(np.size(className)):
        ax[i, j].hist(_x[y==j], bins=15, color = colors[j])
        if (i==0): ax[i, j].set_title(className[j])
        if (j==0): ax[i, j].set_ylabel(cols[i], rotation=0, size='large')
plt.show

<function matplotlib.pyplot.show(close=None, block=None)>

Se Resuelve utilizando el clasificador Naive Bayes de sklearn

Se utiliza el constructor GaussianNB() de la clase GaussianNB para crear el objeto clf_NB

Llamando al método fit del objeto clf_NB se ajusta el modelo contra el conjunto de entrenamiento.

Para validar el modelo se predicen las observaciones X_test del conjunto de validación se comparan las clases obtenidas contra los valores correctos de y_test. El porcentaje de aciertos es la precisión del clasificador

from sklearn.naive_bayes import GaussianNB
clf_NB = GaussianNB()
clf_NB.fit(X_train, y_train)
tot_Test = np.size(y_test)
tot_aciertos = 0
y_pred = []
for x, y in zip(X_test, y_test):
    y_est = clf_NB.predict([x])
    y_pred.append(y_est)
    if (y==y_est): tot_aciertos +=1
    #print('Instancia %s Clase real %s - Clase estimada %s \n' %(x, y, y_est))
print('Exactitud del clasificador (porcentaje de aciertos) = %s \n' %(tot_aciertos*100/tot_Test))

Exactitud del clasificador (porcentaje de aciertos) = 97.36842105263158 

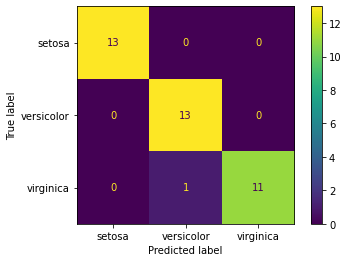
Y la correspondiente matriz de confusión

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
cm=confusion_matrix(y_test, y_pred)
print(cm)

[[13  0  0]
 [ 0 13  0]
 [ 0  1 11]]

from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_true=y_test, y_pred=y_pred)
cm_display = ConfusionMatrixDisplay(cm, display_labels=iris['target_names']).plot()

previous

Capítulo 2: Clasificación

next

02.2 Clasificación naive-Bayes de fronteras intron-exón o exón-intrón de un conjunto de secuencias de DNA