03.2 Clustering - K-Means-Conjunto Iris¶
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
import numpy as np
from skimage import io
from IPython import display
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
output_notebook()
Clasificación de los datos Iris con K-means¶
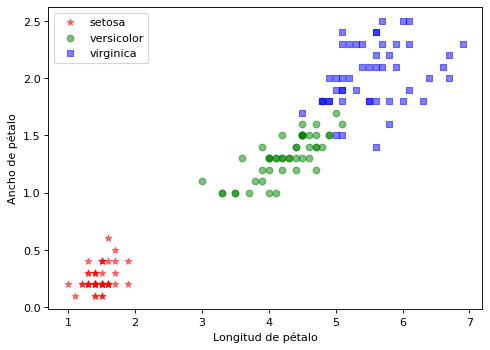
Inicialmente se van a utilizar los 4 atributos del sépalo y pétalo (alto y largo) para clasificar en 3 grupos y mostrar el resultado
from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target']=iris['target']
df.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
X = df.values[:,0:4]
y = df.values[:,4]
import matplotlib.pyplot as plt
clases = iris['target_names']
marcas = ['*', 'o', 's']
color = ['red', 'green', 'blue']
plt.figure(figsize=(7, 5), dpi=80)
for i in range(len(clases)):
plt.scatter(X[y==i,2], X[y==i,3], c=color[i], alpha=0.5, marker=marcas[i], label=clases[i])
plt.xlabel("Longitud de pétalo")
plt.ylabel("Ancho de pétalo")
plt.legend(loc='upper left')
plt.show()
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-04, random_state=1)
y_km = km.fit_predict(X)
Podemos mostrar las coordenadas de los centroides
Directamente mostrando la variable cluster_centers_ que aparece en el objeto que hemos creado con KMeans o algo más vistoso con un DataFrame:
pd.DataFrame(columns=df.columns[0:4],index = np.arange(3),data = km.cluster_centers_)
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| 0 | 6.850000 | 3.073684 | 5.742105 | 2.071053 |
| 1 | 5.006000 | 3.428000 | 1.462000 | 0.246000 |
| 2 | 5.901613 | 2.748387 | 4.393548 | 1.433871 |
Comprobación gráfica de la calidad del clustering¶
Usando matplotlib.pyplot.scatter
Usar un color para las clases predichas por K-means Y una marca para las clases reales de Iris Usar sólo las características del Petalo.
Observamos que K-medias ha asignado 0,1,2 en distintas posiciones. Observamos los graficos y ajustamos la variable clases manualmente para que el gráfico salga bien.
import matplotlib.pyplot as plt
clases = iris['target_names']
####clases = ['virginica','setosa','versicolor']
marcas = ['*', 'o', 's']
color = ['red', 'green', 'blue']
### ... Seguir con el código
import matplotlib.pyplot as plt
clases = iris['target_names']
clases = ['virginica','setosa','versicolor']
marcas = ['*', 'o', 's']
color = ['red', 'green', 'blue']
plt.figure(figsize=(7, 5), dpi=80)
for i in range(len(clases)):
plt.scatter(X[y_km==i,2], X[y_km==i,3], c=color[i], alpha=0.5, marker=marcas[i], label=clases[i])
plt.xlabel("Longitud de pétalo")
plt.ylabel("Ancho de pétalo")
plt.legend(loc='upper left')
plt.show()
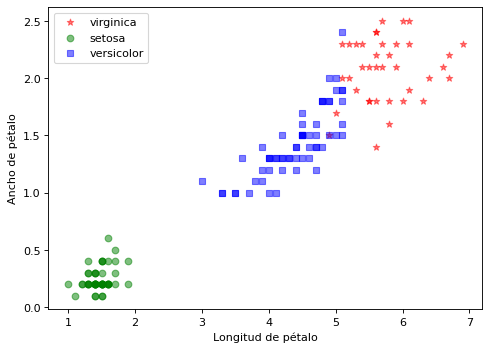
En el dibujo anterior se observan puntos que el Cluster no ha separado bien y que pertenecen a las clases versicolor y virginica
Ratios de Validación Externa¶
Calcular los índices R , ARI , VI y AVI considerando el cluster más perfecto el de 4 características.
from sklearn.metrics.cluster import rand_score
from sklearn.metrics.cluster import adjusted_rand_score
from sklearn.metrics.cluster import mutual_info_score
from sklearn.metrics.cluster import adjusted_mutual_info_score
R=rand_score(labels_true=y, labels_pred=y_km)
ARI=adjusted_rand_score(labels_true=y, labels_pred=y_km)
VI = mutual_info_score(labels_true=y, labels_pred=y_km)
AVI = adjusted_mutual_info_score(labels_true=y, labels_pred=y_km)
R, ARI, VI, AVI
(0.8797315436241611,
0.7302382722834697,
0.8255910976103356,
0.7551191675800485)
Comprobación del número de grupos, diagrama del codo y optimizar el bic()¶
distortions = []
for i in range(1, 11):
km = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
km.fit(X)
distortions.append(km.inertia_)
p = figure(width=500, plot_height=300)
p.line(range(1,11), distortions, line_color="navy", line_width=3, line_alpha=0.6, legend_label="SSE vs k")
p.legend.location='top_left'
p.legend.click_policy="hide"
p.xaxis.axis_label = 'Número de Clusters'
p.yaxis.axis_label = 'Distorsión'
show(p)
from sklearn.mixture import GaussianMixture
bic = []
for i in range(1, 11):
gmm = GaussianMixture(n_components=i, init_params='kmeans')
gmm.fit(X)
bic.append(gmm.bic(X))
p = figure(width=500, plot_height=300)
p.line(range(1,11), bic, line_color="navy", line_width=3, line_alpha=0.6, legend_label="BIC vs k")
p.legend.location='top_left'
p.legend.click_policy="hide"
p.xaxis.axis_label = 'Número de Clusters'
p.yaxis.axis_label = 'BIC'
show(p)
Uso de la matriz de confusión y de la exactitud para realizar la validación¶
Para aplicar la matriz confusión y la Exactitud (Accuracy) es preciso asignar las etiquetas en el Clustering, de forma que las etiquetas predichas se correspondan con las del conjunto Iris
En el conjunto Iris las etiquetas son [‘setosa’, ‘versicolor’, ‘virginica’]
En el clustering han salido en el orden [‘virginica’,’setosa’,’versicolor’]
Hay que hacer las conversiones en la predicción
0 por 2
1 por 0
2 por 1
y_km_new = []
for k in y_km:
if k == 0:
y_km_new.append(2)
elif k == 1:
y_km_new.append(0)
else:
y_km_new.append(1)
y_km_new = np.array(y_km_new)
Repetimos el gráfico anterior usando ya las clases estándar iris[‘target_names’] contra la lista de etiquetas reconvertida
Vemos que sale bien
import matplotlib.pyplot as plt
clases = iris['target_names']
marcas = ['*', 'o', 's']
color = ['red', 'green', 'blue']
plt.figure(figsize=(7, 5), dpi=80)
for i in range(len(clases)):
plt.scatter(X[y_km_new==i,2], X[y_km_new==i,3], c=color[i], alpha=0.5, marker=marcas[i], label=clases[i])
plt.xlabel("Longitud de pétalo")
plt.ylabel("Ancho de pétalo")
plt.legend(loc='upper left')
plt.show()
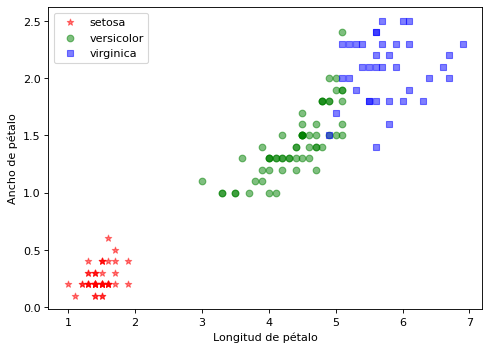
Ya podemos sacar los ratios y la matriz de confusión
from sklearn.metrics import confusion_matrix
confusion_matrix(y, y_km_new)
array([[50, 0, 0],
[ 0, 48, 2],
[ 0, 14, 36]])
Y la exactitud o Accuracy
from sklearn.metrics import accuracy_score
accuracy_score(y_true=y, y_pred=y_km_new)
0.8933333333333333
