4.4 Modelos de Markov Ocultos¶
Idea general:
Generalizan las cadenas de Markov.
Suponemos que existe una cadena de Markov en el modelo pero sus estados no son observables (son ocultos).
Las transiciones ocurren entre estados y las observaciones dependen del estado.
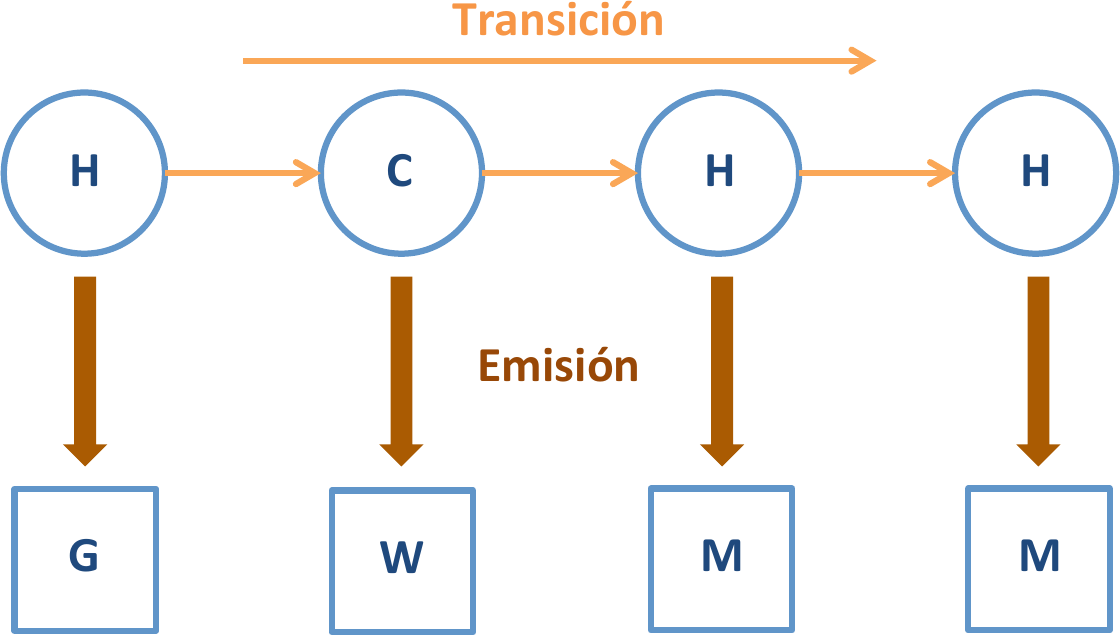
Fig. 10 HMM¶
Ejemplos¶
Sacar bolas de urnas¶
En un cuarto que no es visible para el observador hay un genio. En el cuarto están las urnas \(X_1,X_2,X_3\) cada una de las cuales contiene una mezcla de bolas de colores conocida, y las bolas están numeradas \(s_1,\ldots,s_4\),
El genio elige una urna y saca una bola aleatoriamente de ella. Después muestra la bola al observador, que solamente podrá ver la sucesión de bolas que han sido extraídas.
El genio escoge las bolas con el siguiente procedimiento: la elección de la urna en el paso \(n\) depende únicamente de la urna que escogió en el paso \(n-1\) (proceso de Markov), mientras que la elección de la bola en la urna depende de un número aleatorio.
No podemos observar el proceso de Markov, solamente la sucesión de bolas extraídas.
Adivinar el tiempo¶
Una persona realiza una de tres actividades (dar un paseo, ir de compras o limpiar la casa) en función del tiempo que hace ese día (soleado, lluvioso). Esa persona apunta sus actividades en un diario.
Un investigador, en el futuro, lee el diario de la persona anterior y quiere adivinar el tiempo que hacía cada día.
El tiempo varía según una cadena de Markov, mientras que la elección de la actividad depende de un número aleatorio que varía según el tiempo que hace.
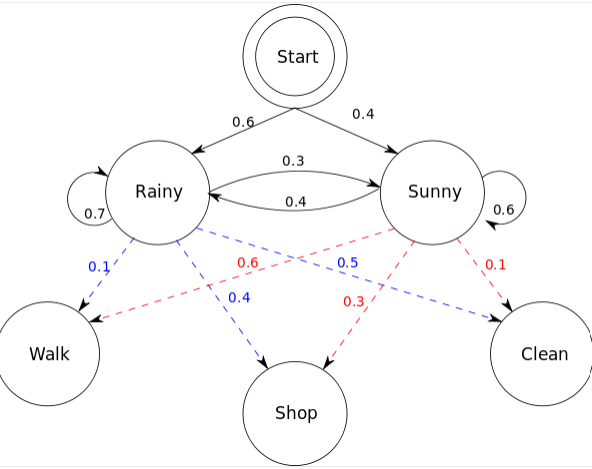
Fig. 11 HMM¶
Estado emocional oculto¶
Un profesor se despierta cada día en uno de tres estados (\(x_1=\)contento, \(x_2=\)triste, \(x_3=\)enfadado). El estado de un día depende únicamente del estado del día anterior. En profesor se pone siempre un jersey de color o verde (\(s_1\)), o azul (\(s_2\)) o marrón (\(s_3\)). La elección del color depende de un número aleatorio que depende del estado en el que se encuentra esa mañana.
Los alumnos conocen la sucesión de estados y colores que ha tenido el profesor a lo largo de lo que llevan de curso. La pregunta que se hacen los alumnos es, dado el color de jersey que lleva el profesor hoy, ¿cuál es su estado emocional?
Aplicación a la estructura secundaria de proteínas¶
Tres estructuras (estados): \(\{H, E , C \}\) (hélice, hoja, resto).
Las transiciones entre estados conforman la estructura secundaria.
En cada paso se emiten sı́mbolos (aminoácidos) que dan lugar a la secuencia observada.
Definiciones HMM¶
Denotaremos como \(X_t\) a los estados (\(X_t\in\mathcal{X}=\{x_1, x_2, \ldots , x_r \}\)) y \(S_t\) a las observaciones (\(S_t\in \mathcal{S}=\{s_1, s_2, \ldots , s_m\}\)) en la iteración \(t\).
Al igual que en cadenas de Markov, necesitamos un vector de probabilidad inicial \(\pi_0\) y una matriz de transiciones \(P\), de dimensión \(r \times r\) , que da las probabilidades condicionadas
Hay que definir las probabilidades de emisión, es decir, la probabilidad condicionada de que el estado \(x_i\) emita el sı́mbolo \(s_j\):
La matriz de emisión es \(E = (e_{ij} )\), donde las filas se refieren a los estados y las columnas a los sı́mbolos emitidos (dimensión \(r \times m\)).
También es estocástica.
Ejemplo HMM¶
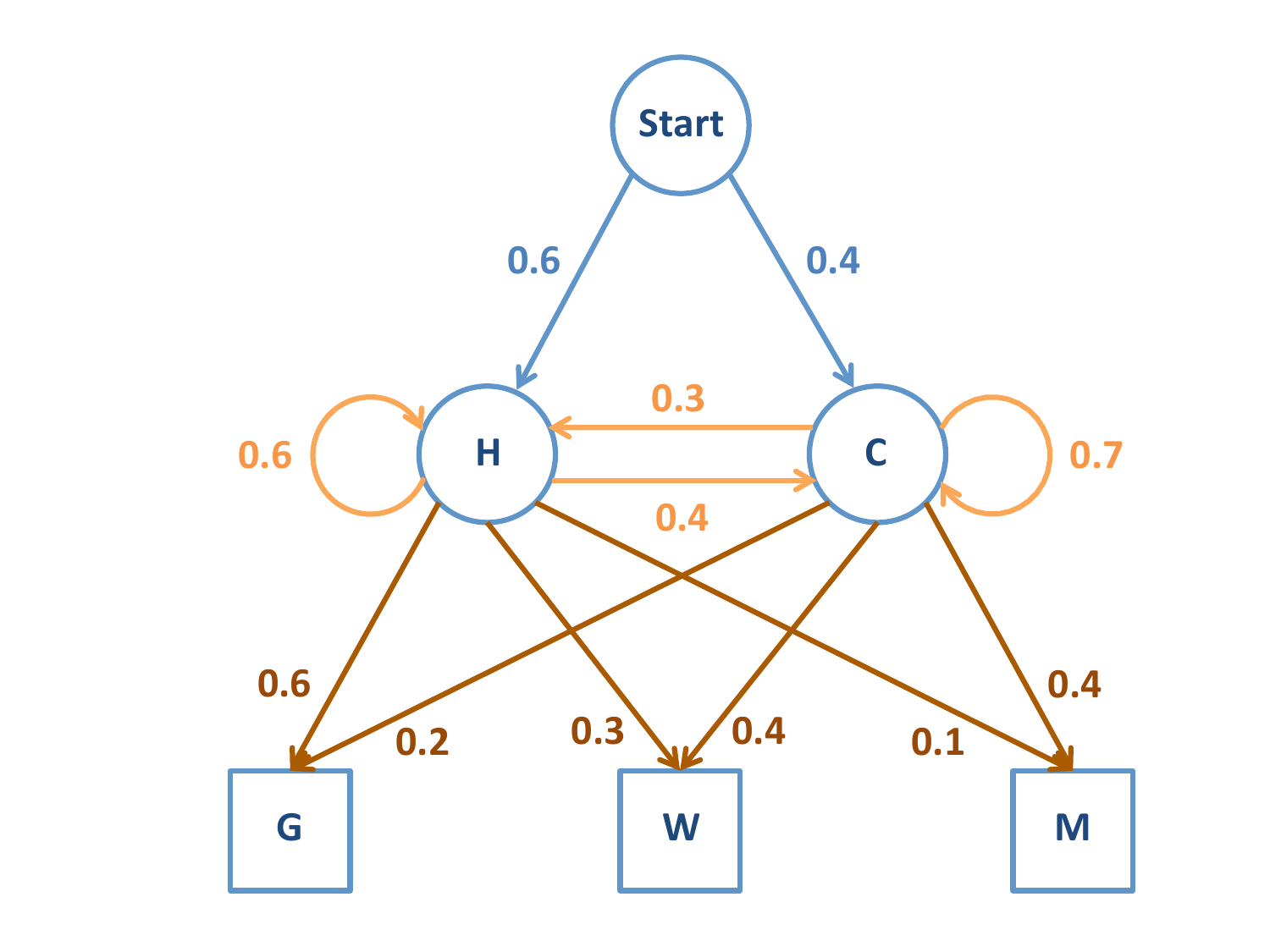
Fig. 12 Esquema de HMM¶
Análisis de un HMM¶
En un modelo de Markov oculto conocemos las secuencias de sı́mbolos \(\{s_1 , s_2 , \ldots , s_n \}\) pero las secuencias de estados son desconocidas en principio.
Tres preguntas básicas:
Aprendizaje: dada una lista de secuencias de sı́mbolos, ¿podemos aprender los parámetros \((\pi^{(0)} , P, E )\) de un HMM? Algoritmo de Baum-Welch.
Evaluación: una vez que el modelo está ajustado, ¿cuál es la verosimilitud de una secuencia dada? Algoritmo “forward”.
Descodificación: una vez que el modelo está ajustado, ¿cuál es el la secuencia de estados más probable para generar de una secuencia de sı́mbolos dada? Algoritmo de Viterbi.
