Práctica 2. Clustering de regiones vinícolas¶
En una práctica anterior ya utilizamos los datos de las características de unos vinos pertenecientes a tres bodegas italianas (fichero de datos wines incorporado a R o wine.csv que se puede encontrar en el libro de la asignatura.
En esta práctica vamos a aplicar un aprendizaje no supervisado como el que propone los mapas auto-organizativo de Kohonen para obtener un agrupamiento de los datos.
Para ello vamos a utilizar uno de los paquetes que están a nuestra disposición en R, el denominado paquete de Kohonen.
Como en la práctica anterior lo primero que hacemos es cargar la librería
Cargar el paquete específico¶
A continuación cargamos el paquete específico que vamos a usar en esta sección para trabajar con mapas auto-organizativos de Kohonen:
library("kohonen")
Carga de los datos.¶
Cargamos el archivo con data("wines") que ya contiene el nombre de cada columna y no incluye la primera de las columnas que indica la bodega a la que pertenecen los datos de cada instancia (fila).
En el caso de los mapas auto-organizativos, donde se va a establecer una relación de proximidad entre los atributos, es conveniente escalar los datos.
Estos datos provienen de
https://archive.ics.uci.edu/ml/datasets/Wine
data(wines)
head(wines,10)
| alcohol | malic acid | ash | ash alkalinity | magnesium | tot. phenols | flavonoids | non-flav. phenols | proanth | col. int. | col. hue | OD ratio | proline |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13.20 | 1.78 | 2.14 | 11.2 | 100 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.40 | 1050 |
| 13.16 | 2.36 | 2.67 | 18.6 | 101 | 2.80 | 3.24 | 0.30 | 2.81 | 5.68 | 1.03 | 3.17 | 1185 |
| 14.37 | 1.95 | 2.50 | 16.8 | 113 | 3.85 | 3.49 | 0.24 | 2.18 | 7.80 | 0.86 | 3.45 | 1480 |
| 13.24 | 2.59 | 2.87 | 21.0 | 118 | 2.80 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735 |
| 14.20 | 1.76 | 2.45 | 15.2 | 112 | 3.27 | 3.39 | 0.34 | 1.97 | 6.75 | 1.05 | 2.85 | 1450 |
| 14.39 | 1.87 | 2.45 | 14.6 | 96 | 2.50 | 2.52 | 0.30 | 1.98 | 5.25 | 1.02 | 3.58 | 1290 |
| 14.06 | 2.15 | 2.61 | 17.6 | 121 | 2.60 | 2.51 | 0.31 | 1.25 | 5.05 | 1.06 | 3.58 | 1295 |
| 14.83 | 1.64 | 2.17 | 14.0 | 97 | 2.80 | 2.98 | 0.29 | 1.98 | 5.20 | 1.08 | 2.85 | 1045 |
| 13.86 | 1.35 | 2.27 | 16.0 | 98 | 2.98 | 3.15 | 0.22 | 1.85 | 7.22 | 1.01 | 3.55 | 1045 |
| 14.10 | 2.16 | 2.30 | 18.0 | 105 | 2.95 | 3.32 | 0.22 | 2.38 | 5.75 | 1.25 | 3.17 | 1510 |
nrow(wines)
Swine<-scale(wines)
head(Swine,10)
| alcohol | malic acid | ash | ash alkalinity | magnesium | tot. phenols | flavonoids | non-flav. phenols | proanth | col. int. | col. hue | OD ratio | proline |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2551008 | -0.50020530 | -0.8221529 | -2.4930372 | 0.02909756 | 0.5710456 | 0.7375437 | -0.8208101 | -0.5370519 | -0.290306650 | 0.4059482 | 1.1284966 | 0.96830550 |
| 0.2056453 | 0.01796903 | 1.1045562 | -0.2748590 | 0.09964918 | 0.8104843 | 1.2181890 | -0.4999191 | 2.1399040 | 0.268966296 | 0.3186634 | 0.8023031 | 1.39703475 |
| 1.7016732 | -0.34832662 | 0.4865552 | -0.8144158 | 0.94626865 | 2.4865554 | 1.4685250 | -0.9812556 | 1.0376281 | 1.181011408 | -0.4232572 | 1.1994082 | 2.33388755 |
| 0.3045563 | 0.22345196 | 1.8316163 | 0.4445501 | 1.29902677 | 0.8104843 | 0.6674496 | 0.2220856 | 0.4077561 | -0.316119247 | 0.3623058 | 0.4619272 | -0.03206274 |
| 1.4914875 | -0.51807338 | 0.3047901 | -1.2940219 | 0.87571703 | 1.5607256 | 1.3683906 | -0.1790282 | 0.6702028 | 0.729290952 | 0.4059482 | 0.3484686 | 2.23861439 |
| 1.7264010 | -0.41979894 | 0.3047901 | -1.4738742 | -0.25310893 | 0.3316069 | 0.4972211 | -0.4999191 | 0.6876992 | 0.083976014 | 0.2750210 | 1.3837785 | 1.73049083 |
| 1.3183934 | -0.16964581 | 0.8864382 | -0.5746128 | 1.51068164 | 0.4912327 | 0.4872077 | -0.4196964 | -0.5895412 | -0.002065978 | 0.4495905 | 1.3837785 | 1.74636969 |
| 2.2704111 | -0.62528187 | -0.7130939 | -1.6537265 | -0.18255731 | 0.8104843 | 0.9578395 | -0.5801419 | 0.6876992 | 0.062465516 | 0.5368753 | 0.3484686 | 0.95242664 |
| 1.0711160 | -0.88436903 | -0.3495639 | -1.0542189 | -0.11200568 | 1.0978108 | 1.1280680 | -1.1417010 | 0.4602454 | 0.931489632 | 0.2313786 | 1.3412315 | 0.95242664 |
| 1.3678488 | -0.16071177 | -0.2405049 | -0.4547113 | 0.38185567 | 1.0499230 | 1.2982965 | -1.1417010 | 1.3875569 | 0.299080993 | 1.2787959 | 0.8023031 | 2.42916072 |
Definición de una malla.¶
La elección de la red bidimensional, tanto en lo que se refiere al número de neuronas como en tipo de entorno, depende del tipo de datos que se esté analizando. En este caso concreto, estamos tratando con instancias que contienen trece atributos y parece conveniente empezar con una malla de \(5 \times 5\) neuronas que denominaremos grid.wine
grid.wine<- somgrid(5,5,"hexagonal")
Generación del mapa auto-organizativo.¶
A partir de los datos escalados recogidos en Swine, entrena las neuronas que forman la red bidimensional recogida en malla.wine mediante el comando específico del paquete kohonen, denominado som:
som.wine<-supersom(Swine, grid = grid.wine)
Medida de la convergencia¶
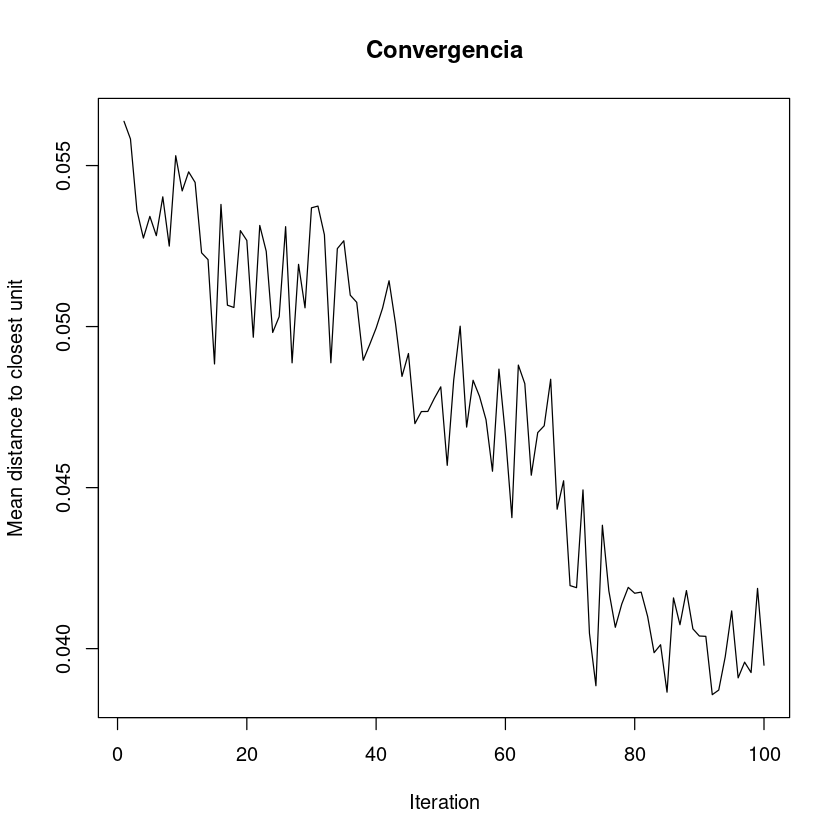
El algoritmo de Kohonen que se implementa en el comando som, converge en un número de pasos razonable (al menos, en los ejemplo sencillos). Para visualizar esta convergencia se suele representar la distancia media a la neurona más cercana frente al número de pasos:
plot(som.wine, type = "changes", main = "Convergencia")
Resumen del mapa SOM¶
Comandos específicos de este paquete permiten obtener un resumen de las caracterísiticas del mapa generado. En concreto, la asignación de cada instancia a una neurona del SOM.
summary(som.wine)
SOM of size 5x5 with a hexagonal topology and a bubble neighbourhood function.
The number of data layers is 1.
Distance measure(s) used: sumofsquares.
Training data included: 177 objects.
Mean distance to the closest unit in the map: 3.69.
print(som.wine$grid)
$pts
x y
[1,] 1.5 0.8660254
[2,] 2.5 0.8660254
[3,] 3.5 0.8660254
[4,] 4.5 0.8660254
[5,] 5.5 0.8660254
[6,] 1.0 1.7320508
[7,] 2.0 1.7320508
[8,] 3.0 1.7320508
[9,] 4.0 1.7320508
[10,] 5.0 1.7320508
[11,] 1.5 2.5980762
[12,] 2.5 2.5980762
[13,] 3.5 2.5980762
[14,] 4.5 2.5980762
[15,] 5.5 2.5980762
[16,] 1.0 3.4641016
[17,] 2.0 3.4641016
[18,] 3.0 3.4641016
[19,] 4.0 3.4641016
[20,] 5.0 3.4641016
[21,] 1.5 4.3301270
[22,] 2.5 4.3301270
[23,] 3.5 4.3301270
[24,] 4.5 4.3301270
[25,] 5.5 4.3301270
$xdim
[1] 5
$ydim
[1] 5
$topo
[1] "hexagonal"
$neighbourhood.fct
[1] bubble
Levels: bubble gaussian
$toroidal
[1] FALSE
attr(,"class")
[1] "somgrid"
getCodes(som.wine)
dim(getCodes(som.wine))
| alcohol | malic acid | ash | ash alkalinity | magnesium | tot. phenols | flavonoids | non-flav. phenols | proanth | col. int. | col. hue | OD ratio | proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | -0.7506273 | -0.91125748 | -1.22750342 | -1.02120578 | -0.21606021 | -0.59679725 | -0.69206448 | 0.43304194 | -1.423662893 | -0.84688682 | 1.193129723 | -0.7675875 | -0.6999783 |
| V2 | -1.5872131 | -0.78563717 | 0.11224968 | 0.99560976 | -1.15971262 | -0.27214066 | -0.24829400 | 0.63627374 | -0.132820057 | -1.15173131 | 1.377160580 | 0.2550838 | -0.6385636 |
| V3 | -0.7853904 | -0.56929828 | -1.14844982 | 0.13656637 | -0.84873827 | -0.22401664 | -0.01541916 | -0.35120228 | -0.176428185 | -0.95421567 | 0.381458956 | 0.6767905 | -0.8399519 |
| V4 | -1.1469936 | -0.24641175 | -0.73775823 | -0.14961426 | -0.35668662 | 1.33571562 | 0.67941807 | -0.99914785 | 1.061795937 | -0.74099128 | 0.583416033 | 0.4657478 | -0.6512454 |
| V5 | -0.5622929 | -0.92839199 | -2.08906110 | -0.99669036 | 0.01800621 | -0.02302554 | 0.19337523 | -0.89159729 | 0.535409264 | -0.54949077 | 1.066986482 | 0.2914826 | -0.6103062 |
| V6 | -0.5859769 | -0.31049079 | -0.73706442 | -0.46541791 | -0.11073907 | -0.85746013 | -1.01098842 | 1.21189791 | -1.066518354 | -0.07135025 | -0.558405229 | -1.0976738 | -0.4658263 |
| V7 | -0.7723909 | -0.45075261 | -0.17799534 | 0.49926650 | -1.03592759 | -1.24895543 | -0.50716213 | 1.44107945 | -0.046987074 | -0.83951992 | 0.065042901 | -0.1145781 | -0.9265405 |
| V8 | -1.1363494 | -0.47299297 | 0.56997470 | 1.64580702 | -0.76007740 | -0.03344100 | 0.26243339 | 0.81467782 | -0.005174655 | -0.99153572 | 0.008041744 | 0.2874269 | -1.0288824 |
| V9 | -1.0956268 | 0.31871269 | 0.20406182 | 0.28256594 | -0.58124918 | 0.57679610 | 0.65426509 | -0.50563032 | 0.828120420 | -0.88293055 | -0.693409963 | 0.8868652 | -0.8077748 |
| V10 | 0.1480213 | 0.40133982 | -0.69287909 | -0.49083005 | -0.07526766 | 0.58817663 | 0.71177236 | -0.63611321 | 0.292128557 | -0.26788955 | -0.135488390 | 0.7420308 | 0.2945765 |
| V11 | -0.2526439 | 0.52633603 | -0.17213610 | 0.10094722 | 0.33107450 | -1.41515205 | -1.15759847 | -0.42350868 | -1.195993366 | 0.11795150 | -1.132332240 | -1.3256552 | -0.2887350 |
| V12 | -0.4197701 | 0.75504536 | 1.01072783 | 0.76288855 | -0.16128206 | -0.78760402 | -1.00805118 | 1.30724984 | -1.147542164 | -0.31417024 | -0.244729571 | -0.4599140 | -0.5305631 |
| V13 | -0.9485642 | 0.69407969 | 1.52559297 | 1.79678388 | 0.57922402 | 0.73269188 | 1.27225327 | 0.56815714 | 0.406796586 | -0.52427341 | 0.241698302 | 0.9637849 | -0.8619558 |
| V14 | 0.3330398 | -0.44200297 | 0.87017765 | -0.05463718 | 0.02723736 | 0.47784077 | 0.64497095 | -0.58474778 | 0.226880030 | -0.33683038 | 0.768414624 | 0.8365250 | 0.3637922 |
| V15 | 0.8255299 | -0.55186960 | -0.21091502 | -1.11123696 | -0.20763557 | 0.35202357 | 0.57235007 | -0.55194695 | 0.102298920 | -0.24122107 | 0.601881375 | 0.7876193 | 1.2954876 |
| V16 | 0.2433786 | 2.11272158 | 0.04380993 | 0.56657001 | -0.75344025 | -1.02859084 | -1.29500344 | 1.32134297 | -0.876918844 | 0.37025387 | -1.048363053 | -1.2610007 | -0.5327505 |
| V17 | 0.4446623 | 1.09437651 | 0.81980067 | 1.22685258 | 0.03118290 | -0.66000678 | -1.33833595 | 1.29997209 | -0.698156479 | 1.04535551 | -1.026205569 | -1.3059678 | -0.1165893 |
| V18 | -0.6221794 | 0.13724625 | 1.22041088 | 0.94731135 | 1.46333844 | -0.53067691 | -0.56754634 | -0.56924497 | -0.060040248 | -0.07043426 | -0.259699746 | -0.4763167 | -0.2772554 |
| V19 | 0.3080877 | -0.36598145 | 1.46607834 | 0.79316168 | 1.93243457 | 0.88577442 | 0.69815450 | 0.08079855 | 0.550444150 | -0.42261244 | 0.931471563 | 0.6953796 | 0.5637818 |
| V20 | 1.2552274 | 0.30387114 | 0.19429157 | -1.04887001 | 1.09649538 | 1.09830560 | 1.03261522 | -0.96127040 | 0.408664605 | 0.17209126 | -0.038224825 | 1.1848853 | 0.6967356 |
| V21 | 0.5525424 | 0.79803298 | -0.07336534 | 0.21108505 | -0.11400609 | -1.04893252 | -1.26370921 | 0.83728954 | -0.498953556 | 1.94266781 | -1.545253665 | -1.4064481 | -0.3228625 |
| V22 | 0.5918879 | 0.44122872 | 1.14530989 | 1.36323018 | 0.66158537 | -0.48652375 | -0.84799224 | -0.08504711 | 0.074405733 | 2.02769446 | -1.401464998 | -1.3665403 | -0.4926906 |
| V23 | 0.5705597 | -0.09866494 | 0.95210123 | 0.70588629 | 1.03229429 | 0.24197552 | 0.06407338 | -0.20096663 | 0.406336633 | 0.90773783 | -0.176898182 | -0.3121957 | 0.3787519 |
| V24 | 0.9589355 | -0.46621233 | 0.72449009 | -0.25893591 | 0.54147972 | 0.96230710 | 1.13829927 | -0.51795417 | 0.847887870 | 0.58296796 | 0.756513410 | 0.4099004 | 1.7460375 |
| V25 | 1.3179012 | -0.59169262 | -0.23516205 | -1.46564591 | 0.14157553 | 1.34547174 | 1.39735533 | -0.74341258 | 1.245160097 | 0.77256095 | 0.422816859 | 0.6662707 | 1.5118687 |
- 25
- 13
print(som.wine$unit.classif)
[1] 15 24 25 19 25 15 20 25 25 24 15 15 25 25 24 24 24 24 20 20 14 15 14 14 19
[26] 15 15 14 15 24 24 15 19 14 14 14 14 15 20 20 10 20 10 10 20 20 25 24 25 25
[51] 24 25 24 20 24 20 24 25 1 1 6 1 4 1 14 5 3 6 5 6 14 3 19 4 1
[76] 5 6 5 13 3 3 2 16 9 3 2 2 2 2 7 7 7 4 4 19 18 5 4 4 5
[101] 3 9 3 3 7 3 7 3 9 4 3 12 2 8 2 3 3 6 3 9 13 13 9 9 3
[126] 9 8 8 12 11 11 11 11 6 6 16 16 16 12 12 11 12 16 11 11 16 16 21 21 22
[151] 22 22 21 6 16 21 17 22 22 16 17 12 11 21 16 22 21 22 22 11 21 21 16 17 21
[176] 21 17
Número de asignaciones a cada neurona¶
Mediante el comando table, obtén una tabla donde aparezcan el número de instancias asignadas a cada neurona. Comenta si se puede asegurar un agrupamiento de los datos a partir de esta tabla.
nb<-table(som.wine$unit.classif)
print(nb)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 24 25
5 7 15 7 6 8 5 3 7 3 9 6 3 10 10 11 4 1 5 10 10 8 13 11
Visualización de los clusters¶
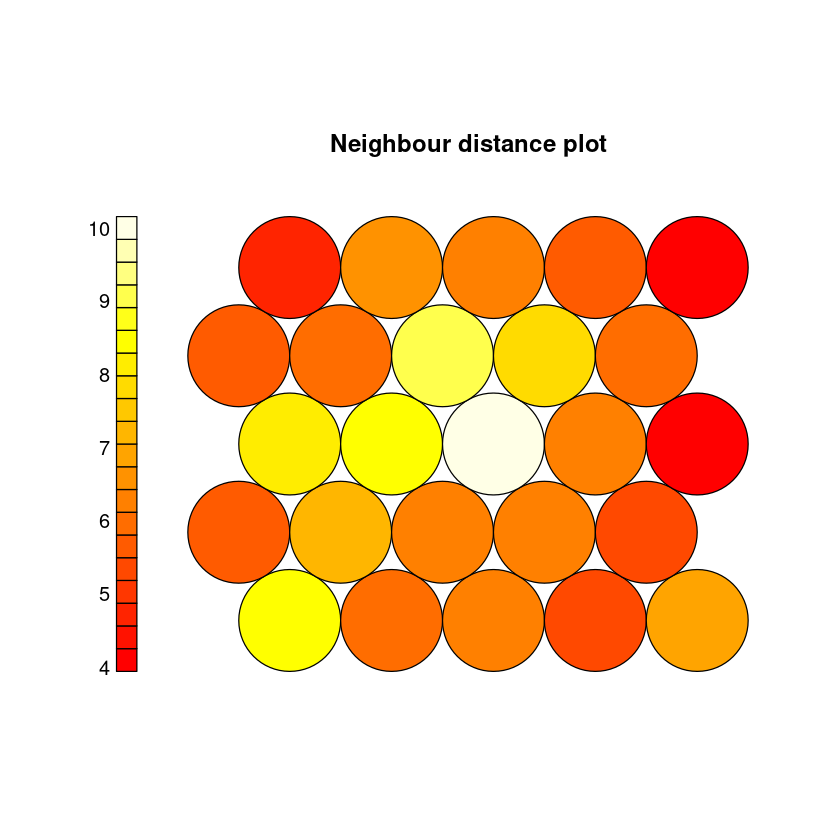
La tabla anterior permite entrever la existencia de un agrupamiento de los datos que, posiblemente, tiene que ver son su distinta fabricación. Sin embargo, este agrupamiento se puede hacer más evidente a partir de las representaciones bidimensionales que están implementadas en el paquete kohonen. En particular, se puede representar la distancia entre vecinos (type= “dist.neighbours”) o el número de instancias que están asociadas a cada neurona (type= “count”)
plot(som.wine, type="dist.neighbours")
Número de instancias asociadas a cada neurona
plot(som.wine, type="count")
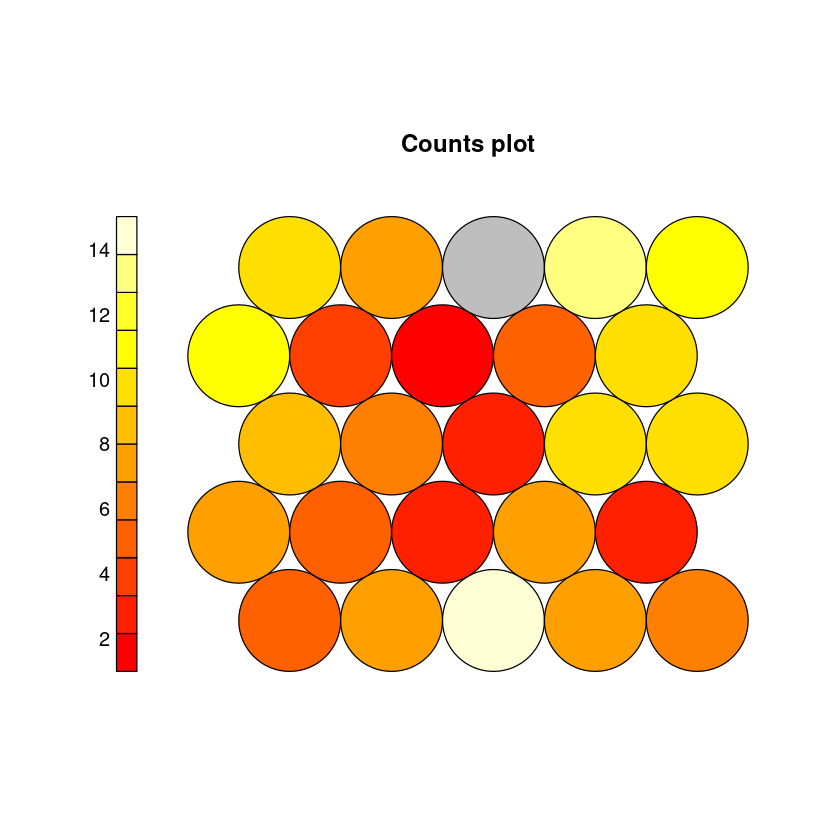
Gráfico de códigos¶
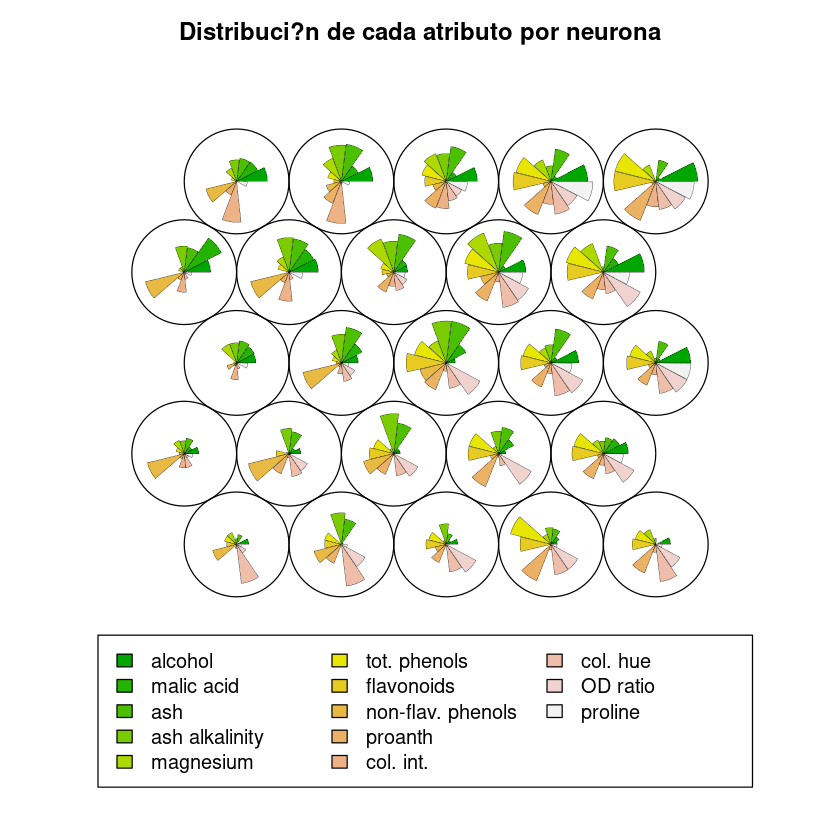
Otro gráfico muy útil para entender el agrupamiento de los datos es el que representa la distribución de los atributos en cada neurona, esto es el vector representativo al que ha convergido cada neurona después del entrenamiento. Haz esta figura y comenta cómo están agrupados los datos en wine.csv.
plot(som.wine, type="codes", codeRendering = "segments", main = "Distribuci?n de cada atributo por neurona")
Warning message in par(opar):
“argument 1 does not name a graphical parameter”
Clustering¶
Podemos realizar un clustering jerárquico con la función hclust de R usando las distancias entre los vectores prototípicos de las neuronas y añadirlo a la representación.
som_cluster<-cutree(hclust(dist(getCodes(som.wine))),3)
som_cluster
- V1
- 1
- V2
- 1
- V3
- 1
- V4
- 1
- V5
- 1
- V6
- 2
- V7
- 1
- V8
- 1
- V9
- 1
- V10
- 3
- V11
- 2
- V12
- 2
- V13
- 3
- V14
- 3
- V15
- 3
- V16
- 2
- V17
- 2
- V18
- 3
- V19
- 3
- V20
- 3
- V21
- 2
- V22
- 2
- V23
- 3
- V24
- 3
- V25
- 3
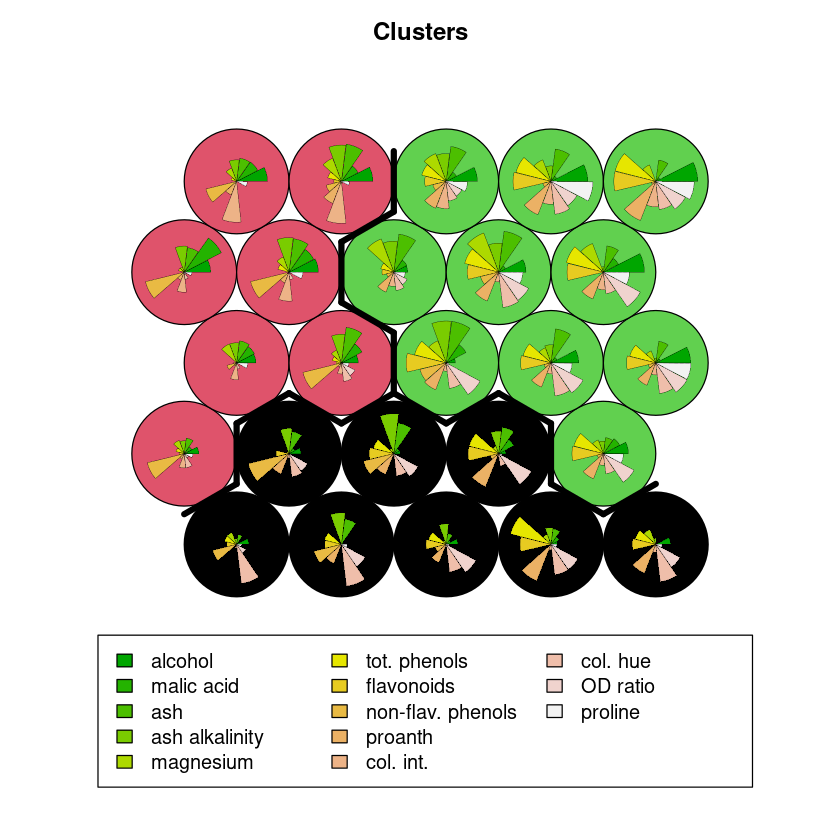
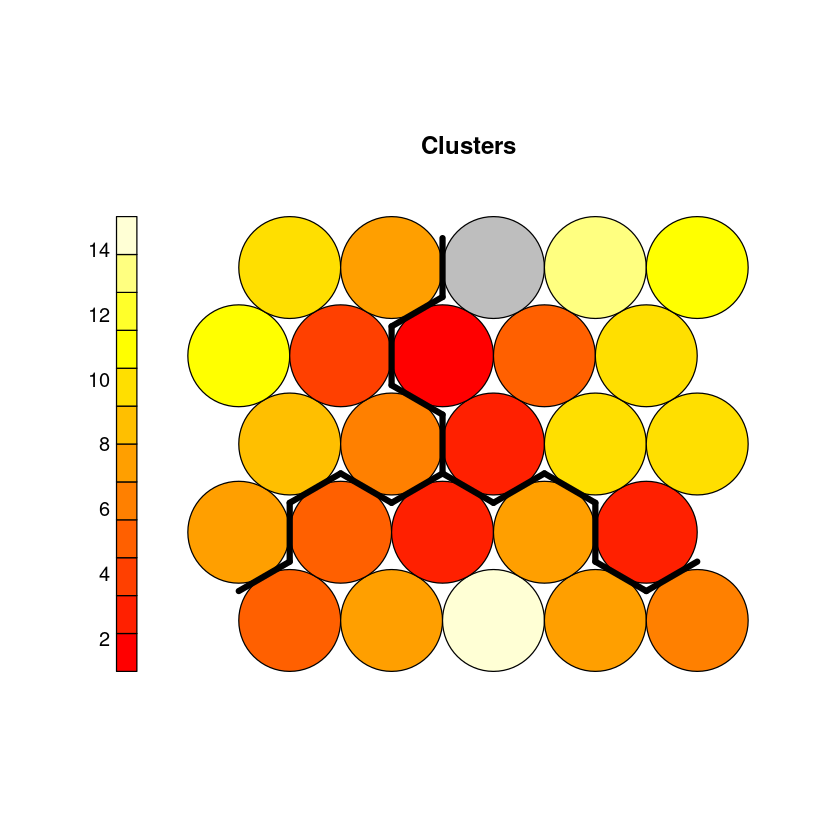
plot(som.wine, type="counts", bgcol = som_cluster, main = "Clusters", col=5)
add.cluster.boundaries(som.wine, som_cluster)
som_cluster <- cutree(hclust(dist(getCodes(som.wine))), 3)
plot(som.wine, type="codes", bgcol = som_cluster, main = "Clusters", col=5)
add.cluster.boundaries(som.wine, som_cluster)
Warning message in par(opar):
“argument 1 does not name a graphical parameter”