4.1B Otros ejemplos¶

La ruina del apostador¶

Una persona apuesta en un juego en el cual puede, o bien ganar 1€ con probabilidad \(p\), o perder 1€ con probabilidad \(1-p\). El jugador comienza con \(k\)€, y el juego termina cuando, o bien pierda todo su dinero, o bien alcance una suma de \(n\)€.

Espacio de estados:

\[ \mathcal{X}=\{0,1,\ldots,n\} \]

Probabilidades de transición

\[\begin{split} p_{ij}=\begin{cases} p&\text{ si }j=i+1,& 0<i<n,\\ 1-p&\text{ si }j=i-1,&0<i<n,\\ 1&\text{ si } i=j=0,&\text{ ó }i=j=n, \\0&\text{ otro caso} &\\ \end{cases} \end{split}\]

Caso \(n=5\), \(p=0.4\)

\[\begin{split} P=\begin{pmatrix}1&0&0&0&0&0\\ 0.6&0&0.4&0&0&0\\ 0&0.6&0&0.4&0&0\\ 0&0&0.6&0&0.4&0\\ 0&0&0&0.6&0&0.4\\ 0&0&0&0&0&1 \end{pmatrix} \end{split}\]

Preguntas:

Cuál es la probabilidad que el jugador gane o pierda?
Después de un número \(m\) de juegos, ¿cuál es la cantidad media de dinero que tiene el jugador?

Paseo aleatorio en un grafo dirigido con pesos¶

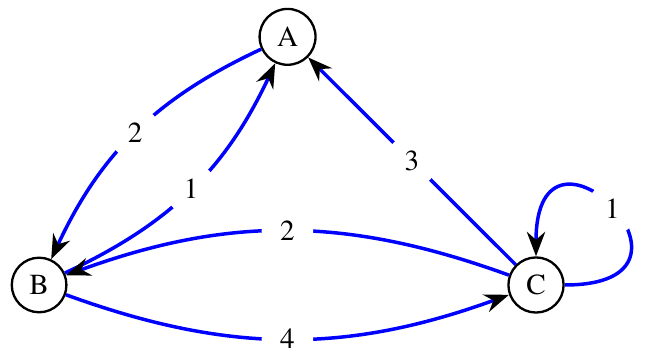
Fig. 6 Grafo dirigido con pesos¶

Una cadena de Markov puede ser representada como un paseo aleatorio en un grafo dirigido con pesos en las aristas. Esto es un grafo en el que cada arista tiene asignado un número real positivo, su peso, y el paseante aleatorio elige una arista del conjunto de aristas disponibles, en proporción al peso de cada arista. Un grafo dirigido es aquel que cada arista también tiene una dirección, y el paseante puede moverse en esa dirección.

Matriz de transición

\[\begin{split} P=\begin{pmatrix}0&1&0\\1/5&0&4/5\\3/6&2/6&1/6\end{pmatrix} \end{split}\]

Este tipo de grafos está en los inicios del algoritmo Page Rank de Google, que ha revolucionado las búsquedas en internet.

La pulga saltarina¶

Una pulga se encuentra saltando aleatoriamente entre diferentes puntos de una mesa de acuerdo con el esquema y probabilidades de la figura.

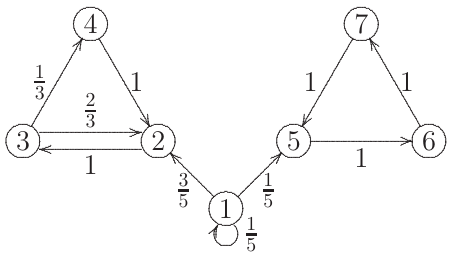
Fig. 7 Esquema de saltos de la pulga saltarina¶

Hay 7 puntos donde la pulga puede estar.

El espacio de estados es

\[ \mathcal{X}=\{1,2,3,4,5,6,7\} \]

Preguntas:¶

Empezando desde el estado 1, cuál es la probabilidad de llegar al estado 7 en algún momento?
Empezando desde el estado 2, cuál es el tiempo esperado para llegar al estado 4?
Empezando desde el estado 2, cuál es la proporción de tiempo a largo plazo que la pulga pasa en el estado 3?
Empezando por el estado 1, cuál es la probabilidad de estar en el estado 2 en el tiempo \(t\)? Converge esta probabilidad si \(t\to\infty\)? Y, si lo hace, a qué valor?
¿Cuál es la probabilidad de la trayectoria 1,2,3,2,3,4?

Tirar una moneda¶

El ejercicio de tirar una moneda y ver el resultado sucesivas veces es un ejemplo canónico del proceso de ensayos de Bernoulli independientes. No obstante en [Diaconis et al., 2007] se estudió este proceso empíricamente y se encontro que los resultados de tirar una moneda sucesivas veces no son independientes. En cambio, se pueden modelizar como una cadena de Markov con la siguiente matriz de transición

\[\begin{split} P=\begin{matrix}heads\\tails\end{matrix}\begin{pmatrix}0.51&0.49\\0.49&0.51\end{pmatrix} \end{split}\]

Esto significa que si sacas cara en un lanzamiento, la probabilidad de obtener cara en un segundo lanzamiento es ligeramente mayor que obtener cruz.

Conductores¶

Una empresa de seguros de coche clasifica a los conductores como bajo riesgo si no han tenido accidentes en el último año. Los datos históricos muestran que el 98% de los conductores en la categoría bajo riesgo (L) seguirán estando en la misma categoría al año siguientes, y el 78% de los conductores que no están en la categoría de bajo riesgo (L’) un año estarán en la categoría de bajo riesgo el año siguiente.

\[ \mathcal{X}=\{L,L'\} \]

\[\begin{split} P=\begin{pmatrix}0.98 & 0.02\\0.78 & 0.22\end{pmatrix} \end{split}\]

Pregunta:

Si el 90% de los conductores en la comunidad son de la categoría de bajo riesgo este año, ¿cuál es la probabilidad que un conductor elegido al azar de la comunidad sea de bajo riesgo el año que viene? ¿Y el año siguiente?

El Lenguaje¶

El propósito de Andrei Markov era el estudio de la distribución de letras en la poesía Rusa. Construyó una lista de las frecuencias de las transiciones entre parejas de letras (vocal/consonante) de las 20.000 primeras letras del poema Eugene Onegin de Pushkin, y construyó una matriz de transición

\[\begin{split} P=\begin{matrix}vocal\\consonante\end{matrix}\begin{pmatrix}0.175&0.828\\0.526&0.474\end{pmatrix} \end{split}\]

Mostró cómo es posible hallar, a partir de esta matriz, el número medio de vocales y consonantes. A partir de esta matriz es posible reconstruir texto con un aspecto realista. [Hayes, 2013].

Aplicación de Cadena de Markov¶

Esta aplicación puede verse en [Rogers et al., 2013].

Se modelizó el espacio de configuración de dos coloides recubiertos de ADN como una cadena de Markov de dos estados, con espacio de estados

\[ \mathcal{X}=\{bound,unbound\} \]

en función de la distancia entre las partículas.

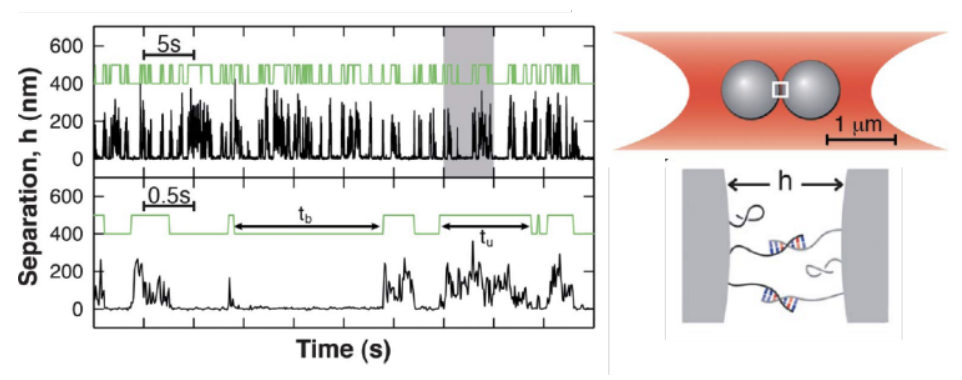
Fig. 8 Esquema del modelo de Markov aplicado a la separación de coloides.¶

Otros ejemplos¶

Se han usado cadenas de Markov en:

random walks
modelización de procesos físicos
- predicción de lluvias
- dinámica de poblaciones
- folding de proteínas
- sistemas de colas:
  - colas de supermercados
  - servidores informáticos
  - llamadas a un servicio
  - call centers
- reacciones químicas
- estadísticas deportivas
discretizar un sistema continuo
tomar muestras de sistemas de alta dimensión: Markov-Chain Monte-Carlo
análisis de datos y redes
- clustering
- reconocimiento de voz
- algoritmo Page Rank del motor de búsqueda de Google

Introducción al Aprendizaje Automático