.ipynb .pdf

Contents

6.5 Ejemplo con Datos demográficos

Warning

Este cuaderno está realizando con código R

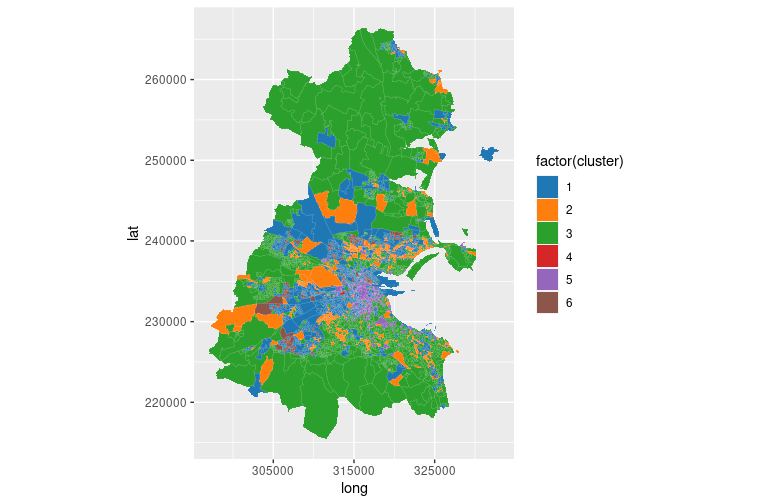
• Datos: censo irlandés, area de Dublín, año 2011

• Algoritmo SOM en R

• Visualización de los resultados

Referencia online

Los códigos R y los datos originales están en el repositorio GIT

Los datos cocinados en: dataIrelandPopulationSOM.csv

Carga y descripción de los datos

require(kohonen)

Loading required package: kohonen

data<-read.csv("./data/dataIrelandPopulationSOM.csv")

typeof(data)

'list'

head(data,10)

A data.frame: 10 × 15

	X	id	avr_age	avr_household_size	avr_education_level	avr_num_cars	avr_health	rented_percent	unemployment_percent	internet_percent	single_percent	married_percent	separated_percent	divorced_percent	widow_percent
	<int>	<chr>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	15687	267123023	40.02811	2.524752	3.038462	1.0396040	4.385542	6.930693	15.343915	71.00000	53.41365	33.33333	4.8192771	2.8112450	5.6224900
2	13895	267016001	35.67366	3.320611	3.597701	1.9837398	4.509434	4.878049	12.461059	72.95082	49.41725	44.98834	1.3986014	0.2331002	3.9627040
3	13896	267016002	35.88235	3.324324	4.295302	1.9054054	4.596639	1.351351	10.404624	83.78378	47.47899	43.69748	3.3613445	0.0000000	5.4621849
4	13729	267002034	38.51667	3.088608	3.871795	1.7307692	4.530172	3.896104	8.108108	78.94737	47.08333	48.33333	0.8333333	1.2500000	2.5000000
5	13724	267002029	24.67800	3.512000	3.933735	1.1120000	4.510345	20.800000	21.810700	81.30081	67.12018	26.98413	2.2675737	1.5873016	2.0408163
6	13739	267002044	25.13953	3.136364	4.496855	1.1090909	4.419162	29.357798	24.154589	81.90476	64.24419	30.23256	1.4534884	3.4883721	0.5813953
7	13725	267002030	25.05882	3.441176	4.726872	1.5588235	4.689888	23.529412	8.680556	94.11765	55.55556	36.81917	3.7037037	2.8322440	1.0893246
8	13710	267002015	24.43733	2.861538	3.973510	0.9692308	4.580556	4.687500	19.457014	81.25000	70.40000	21.33333	2.9333333	3.4666667	1.8666667
9	13712	267002017	23.50530	2.958763	4.674242	1.3917526	4.685921	20.618557	14.044944	91.75258	62.54417	32.86219	2.4734982	1.7667845	0.3533569
10	13713	267002018	24.67355	2.928571	4.530769	1.4047619	4.579832	14.814815	10.897436	82.92683	66.52893	29.75207	1.6528926	1.6528926	0.4132231

names(data)

1. 'X'
2. 'id'
3. 'avr_age'
4. 'avr_household_size'
5. 'avr_education_level'
6. 'avr_num_cars'
7. 'avr_health'
8. 'rented_percent'
9. 'unemployment_percent'
10. 'internet_percent'
11. 'single_percent'
12. 'married_percent'
13. 'separated_percent'
14. 'divorced_percent'
15. 'widow_percent'

dim(data)

1. 4806
2. 15

Selección de datos y tratamiento

Hacemos una subselección de las variables al conjunto 2,4,5,8.

Centramos y escalamos las variables para que tengan igual importancia durante el proceso SOM

Convertimos los datos a una matriz

c(2,4,5,8)+1

1. 3
2. 5
3. 6
4. 9

names(data)[c(2,4,5,8)+1]

1. 'avr_age'
2. 'avr_education_level'
3. 'avr_num_cars'
4. 'unemployment_percent'

data_train <- data[,c(2,4,5,8)+1]
head(data_train,10)

A data.frame: 10 × 4

	avr_age	avr_education_level	avr_num_cars	unemployment_percent
	<dbl>	<dbl>	<dbl>	<dbl>
1	40.02811	3.038462	1.0396040	15.343915
2	35.67366	3.597701	1.9837398	12.461059
3	35.88235	4.295302	1.9054054	10.404624
4	38.51667	3.871795	1.7307692	8.108108
5	24.67800	3.933735	1.1120000	21.810700
6	25.13953	4.496855	1.1090909	24.154589
7	25.05882	4.726872	1.5588235	8.680556
8	24.43733	3.973510	0.9692308	19.457014
9	23.50530	4.674242	1.3917526	14.044944
10	24.67355	4.530769	1.4047619	10.897436

data_train_matrix <- as.matrix(scale(data_train))

#''''''

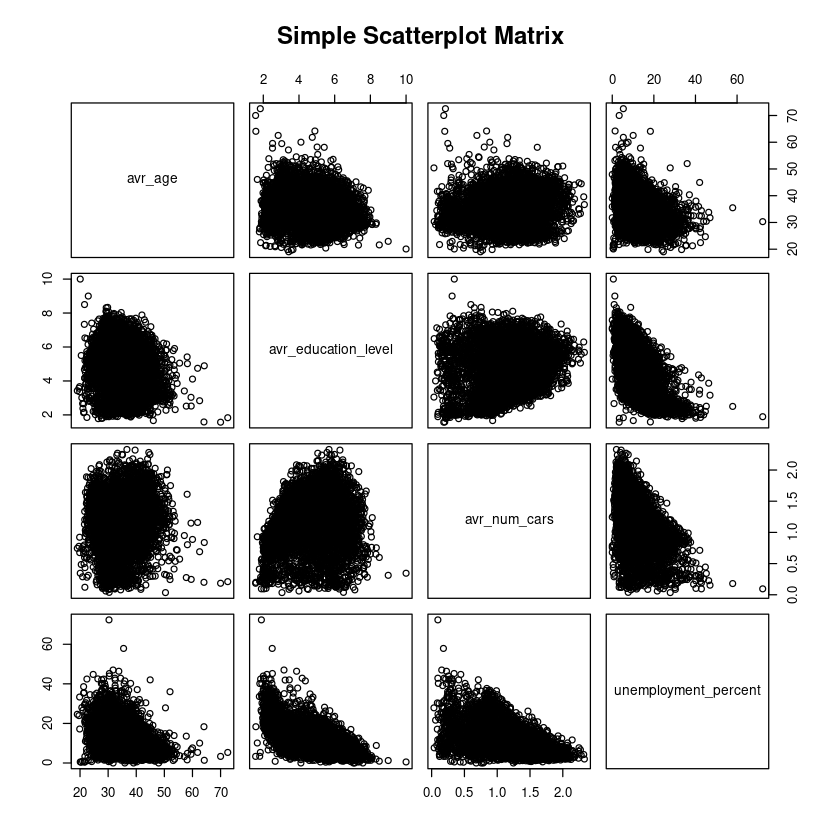
pairs(~avr_age+avr_education_level+avr_num_cars+unemployment_percent,data=data,
   main="Simple Scatterplot Matrix")

Definir y entrenar el SOM

Creamos el SOM grid con topología hexagonal, y tamaño \(20\times20\).

Entrenamos el SOM usando el grid anterior. Usamos las opciones por defecto del paquete.

som_grid <- somgrid(xdim = 20, ydim=20, topo="hexagonal")

som_model <- som(data_train_matrix, 
    grid=som_grid, 
    rlen=500, 
    alpha=c(0.05,0.01), 
    keep.data = TRUE )

Visualizar los datos

coolBlueHotRed <- function(n, alpha = 1) {
  rainbow(n, end=4/6, alpha=alpha)[n:1]
}

pretty_palette <- c("#1f77b4", '#ff7f0e', '#2ca02c', '#d62728', '#9467bd', '#8c564b', '#e377c2')

Progreso del entrenamiento

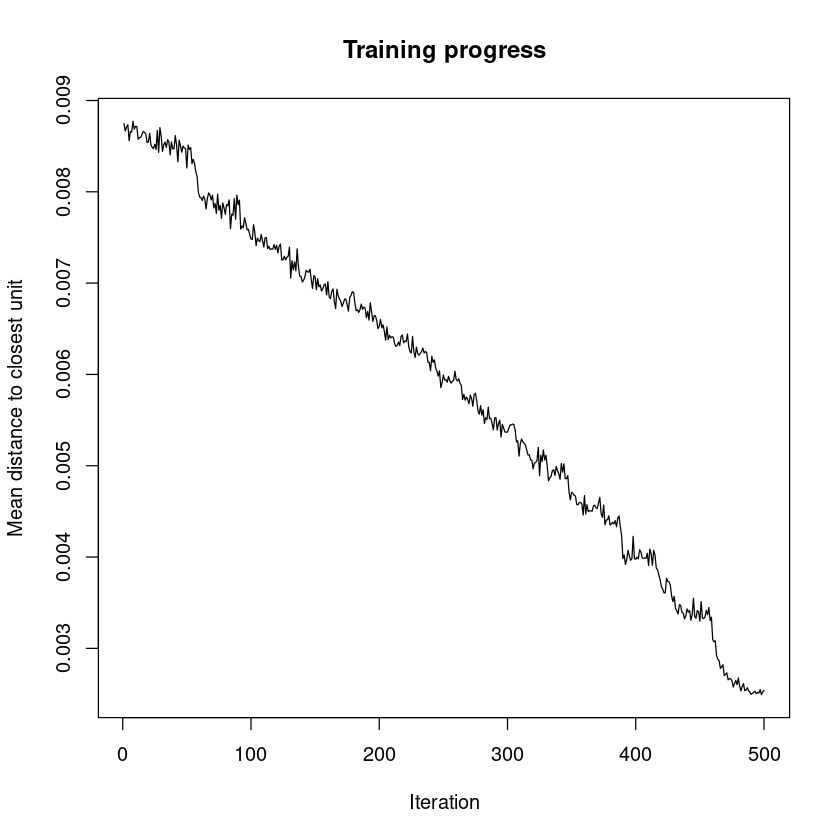
A medida que avanza el entrenamiento, la distancia de los pesos de cada nodo a los inputs asociados a dicho nodo se reduce. Idealmente esta distancia debería alcanzar un plateau mínimo.

Si la curva sigue decreciendo quizás son necesarias más iteraciones o cambiar los parámetros de las funciones de aprendizaje y núcleo de vecindad.

plot(som_model, type = "changes")

Conteo por nodo

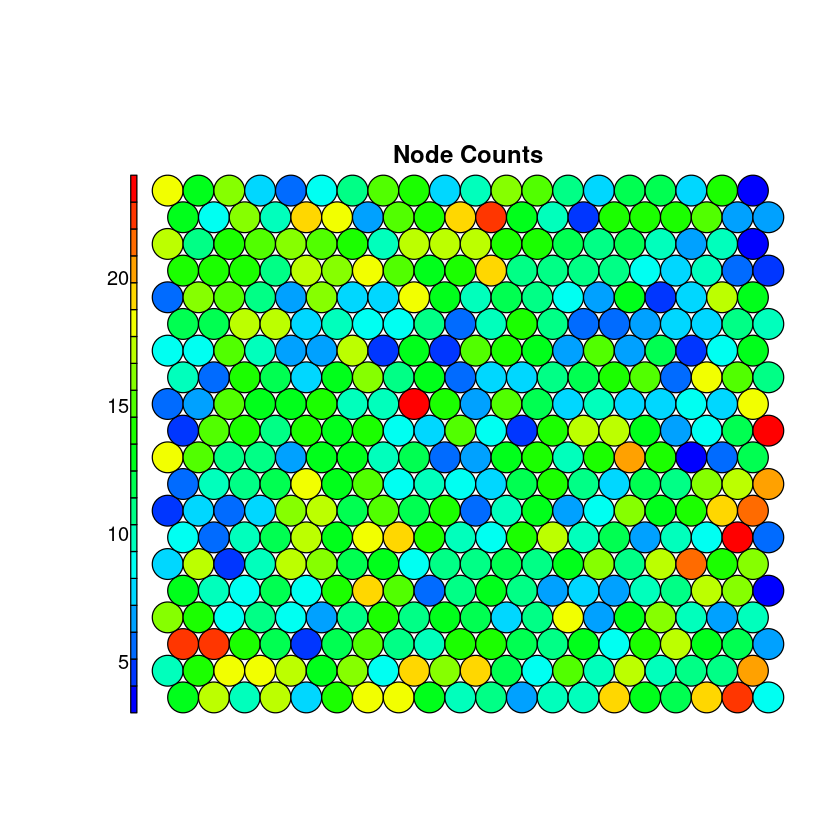
Visualizar el número de datos de entrada que están asociados a cada nodo en el mapa.

Esto puede ser usado como una medida de la calidad del mapa:

• valores altos en ciertas áreas del mapa sugieren que un mapa más grande puede ser adecuado

• muchos nodos vacíos indican que el mapa es demasiado grande

plot(som_model, type = "counts", main="Node Counts", palette.name=coolBlueHotRed)

plot(som_model, type="mapping", main = "Mapeo de puntos", palette.name=coolBlueHotRed)

plot(som_model, type = "quality", main="Node Quality/Distance", palette.name=coolBlueHotRed)

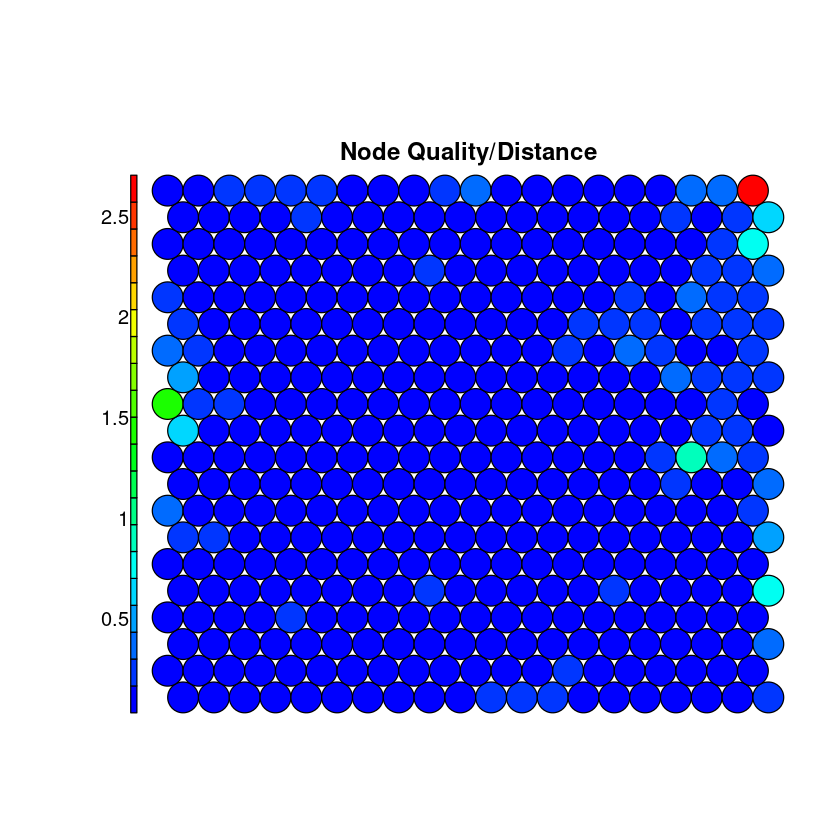
U-matrix

La \(U\)-matrix es una representación de las distancias entre los nodos.

Áreas donde la distancia entre vecinos sea baja indican grupos de nodos que son similares.

Áreas con grandes distancias entre nodos marcan diferencias e indican fronteras naturales entre los clusters de nodos.

plot(som_model, type="dist.neighbours", main = "SOM neighbour distances", palette.name=grey.colors)

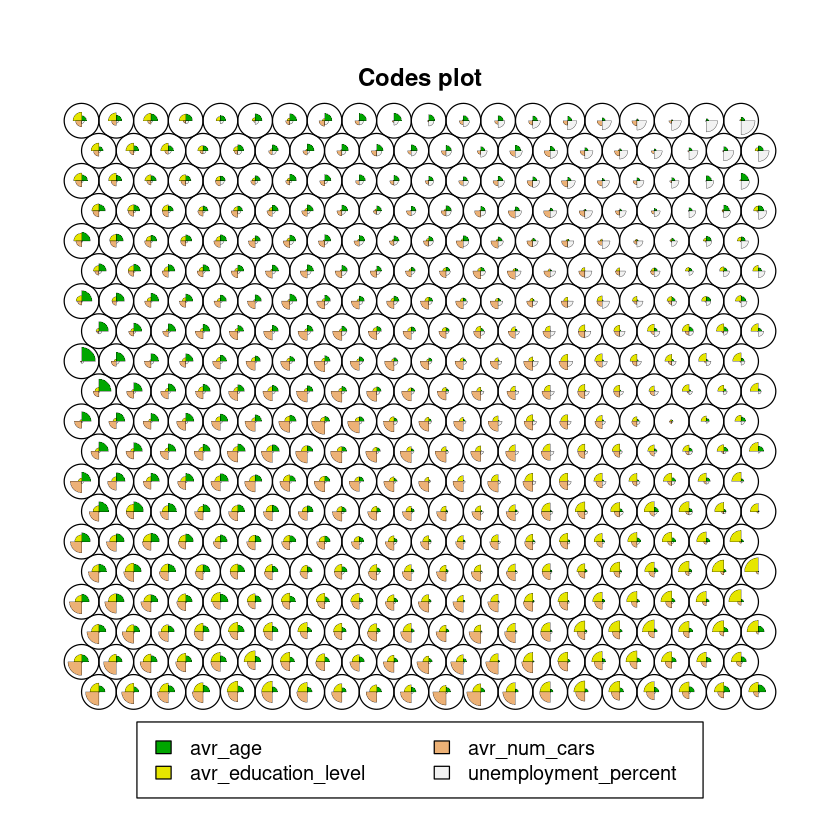
Mápa de códigos

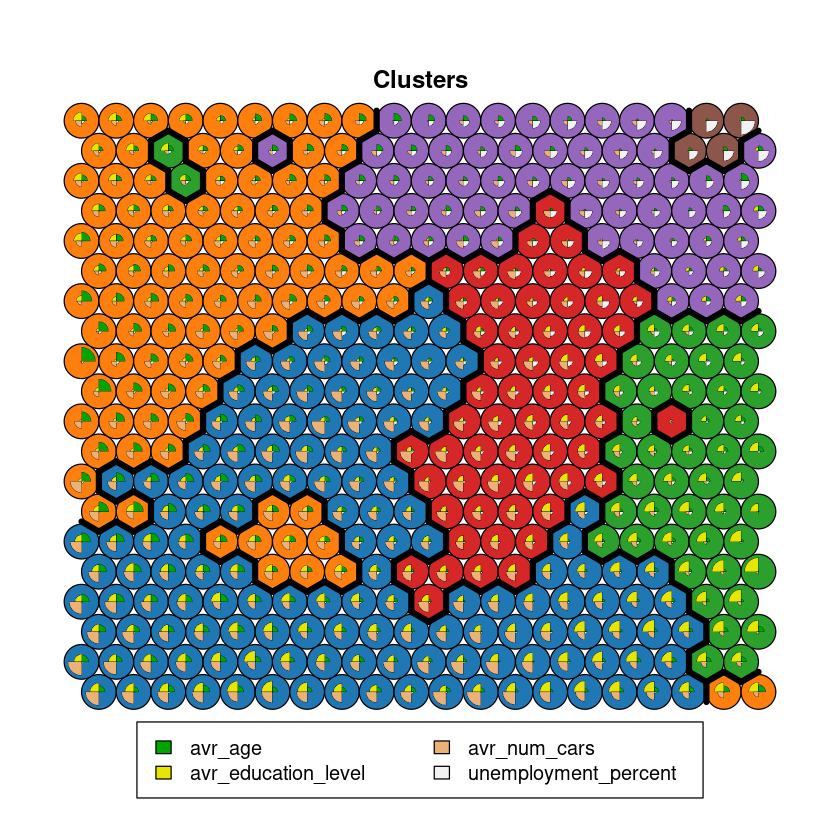
En el siguiente mapa, para cada nodo, se representa un diagrama con información de su vector prototipo. En este caso son valors normalizados de los valores originales y, por tanto, se pueden comparar.

Cada vector de pesos de cada nodo es representativo (similar) a los de los datos que están asociados a dicho nodo.

Esta visualización permite enconrtar patrones en la distribución de muestras y variables.

Existe varias opciones para realizar esta presentación.

plot(som_model, type = "codes")

Warning message in par(opar):
“argument 1 does not name a graphical parameter”

Mapas de calor: heatmaps

Los mapas de calor adquieren una especial relevancia en los SOM. El enfoque anterior de presentar los mapas de códigos para cada nodo se vuelve inviable para datos en alta dimensión.

Un mapa de calor permite visualizar la distribución de una variable sobre el mapa.

Recordatorio: los datos de entrada están fijados a su nodo correspondiente, no se mueven. Lo que visualizamos es la distribución de cada uno de sus atributos en el mapa.

var <- 2
plot(som_model, 
     type = "property", 
     property = getCodes(som_model)[,var], 
     main=colnames(getCodes(som_model))[var], 
     palette.name=coolBlueHotRed
)

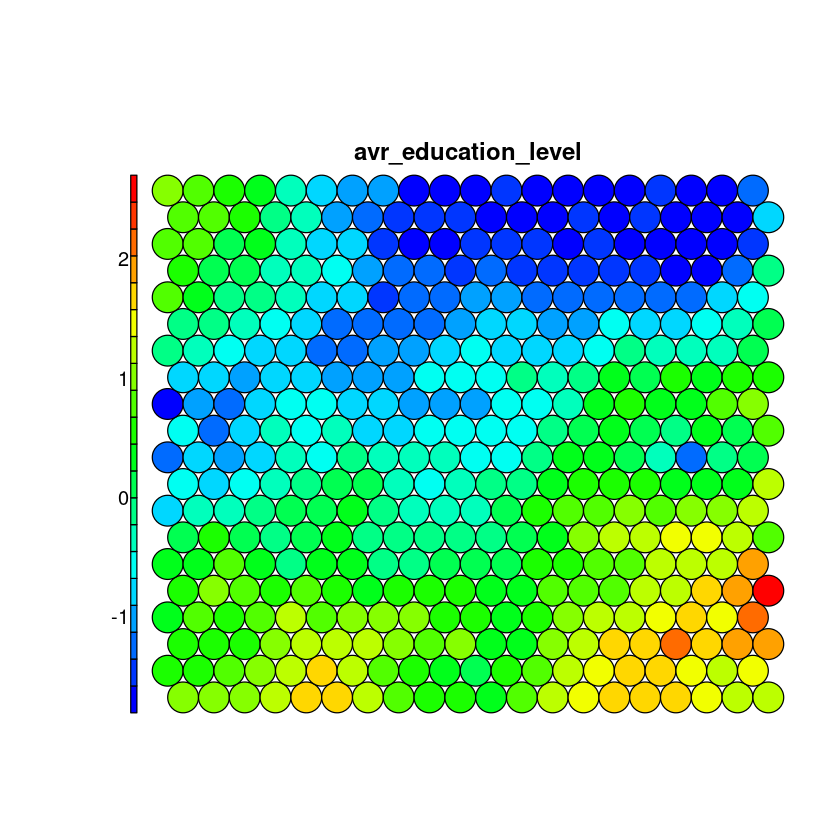
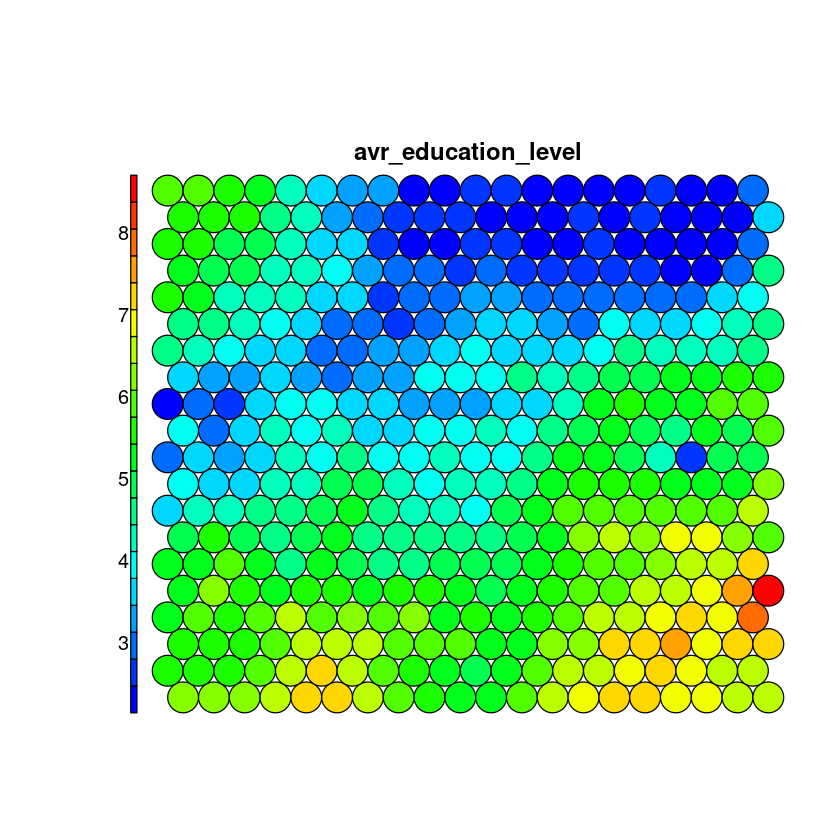
La visualización anterior es de la versión normalizada de la variable de interés. Podemos desnormalizarla.

var <- 2 
var_unscaled <- aggregate(as.numeric(data_train[,var]), by=list(som_model$unit.classif), FUN=mean, simplify=TRUE)[,2]
plot(som_model, type = "property", property=var_unscaled, main=names(data_train)[var], palette.name=coolBlueHotRed)
rm(var_unscaled)

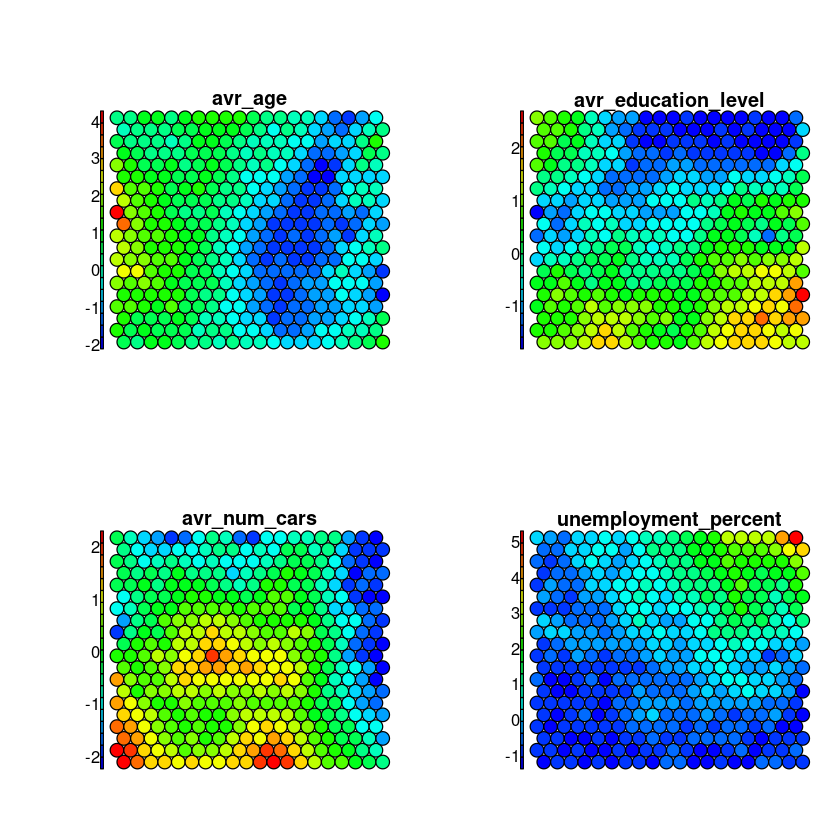
Podemos hacer varios mapas de calor y acumularlos para compararlos visualmente

par(mfrow=c(2,2))
for(var in c(1,2,3,4)){
plot(som_model, 
     type = "property", 
     property = getCodes(som_model)[,var], 
     main=colnames(getCodes(som_model))[var], 
     palette.name=coolBlueHotRed
)       
}

Clustering de los resultados

Podemos realizar un algoritmo de clustering sobre el conjunto de los vectores prototipo de los nodos.

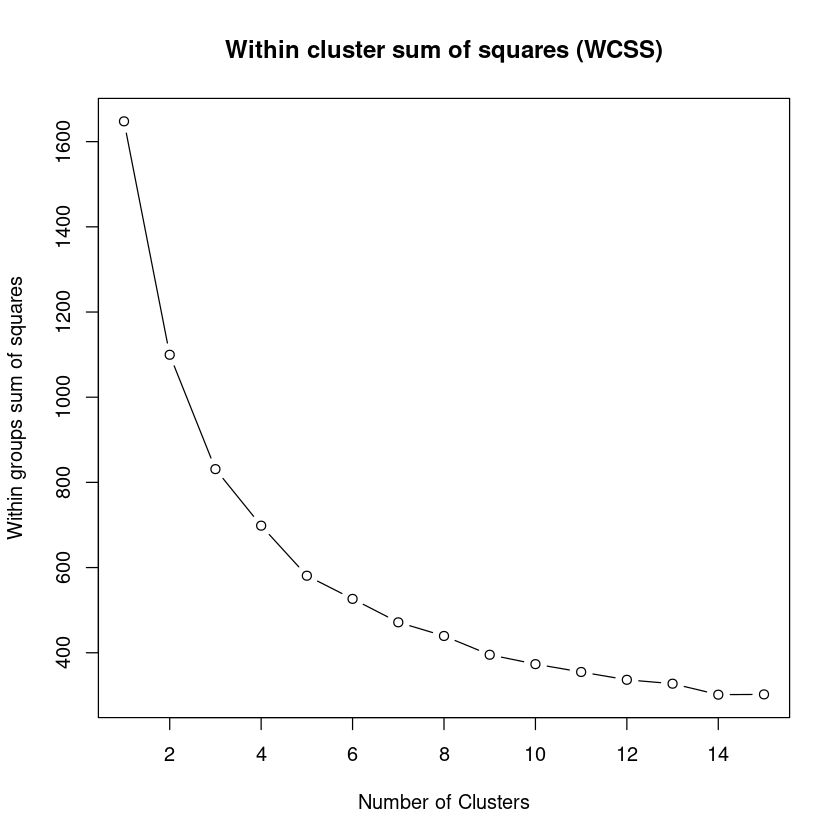
Realizamos una gráfica para averiguar el número de clusters a través de sucesivas aplicaciones de \(k-means\) usando la métrica dada por el WCSS

Después realizamos un hierarchical clustering hclust con el número óptimo que nos indica la gráfica.

Añadimos finalmente la información de los clusters al mapa SOM.

mydata <- getCodes(som_model)
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(mydata,
                                     centers=i)$withinss)
par(mar=c(5.1,4.1,4.1,2.1))
plot(1:15, wss, type="b", xlab="Number of Clusters",
     ylab="Within groups sum of squares", main="Within cluster sum of squares (WCSS)")

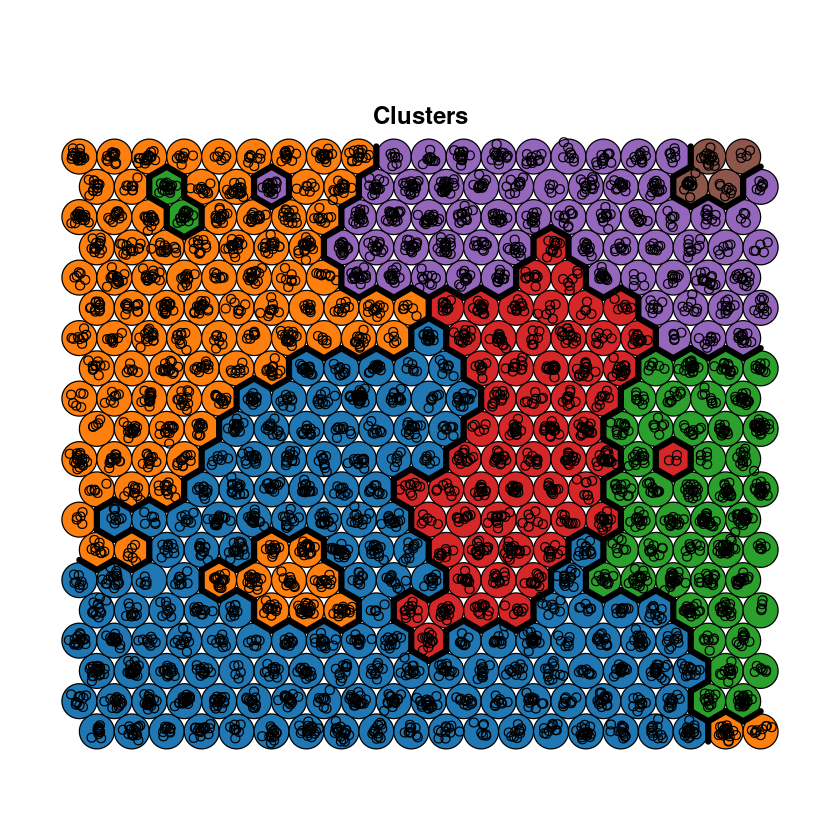
som_cluster <- cutree(hclust(dist(getCodes(som_model))), 6)

plot(som_model, type="mapping", bgcol = pretty_palette[som_cluster], main = "Clusters")
add.cluster.boundaries(som_model, som_cluster)

plot(som_model, type="codes", bgcol = pretty_palette[som_cluster], main = "Clusters")
add.cluster.boundaries(som_model, som_cluster)

Warning message in par(opar):
“argument 1 does not name a graphical parameter”

Clústeres sobre el mapa topográfico

Si los datos contienen información GIS, es posible representar qué puntos del mapa topográfico de Dublín están relacionados con qué clústeres.

Fig. 37 Geolocalización de los clústeres hallados

previous

6.4 Aplicaciones en biotecnología

next

6.6 Ejemplo con Colores RGB