import numpy as np
import matplotlib.pyplot as plt
6.6 Ejemplo con Colores RGB¶
Codificación R(ed)G(reen)B(lue) para los colores en informática
En este enlace puedes seleccionar un color a ojo y obtener su valor RGB
Colores cercanos tendrán valores RGB cercanos
Funciones del SOM¶
Usaremos un SOM bidimensional con m x n celdas.
Usaremos un array bidimensional más un eje donde colocaremos los pesos correspondientes a los canales R, G y B, es decir, un vector de tres componentes de números enteros en el intervalo \([0,255]\).
La función find_BMU devuelve las coordenadas (en el grid) de la neurona BMU dado el mapa SOM y el vector de datos de entrenamiento x.
Los inputs son el mapa SOM y el vector de entrenamiento.
Devuelve las coordenadas \((g,h)\) de la BMU en el grid.
def find_BMU(SOM,x):
distSq = (np.square(SOM - x)).sum(axis=2)
return np.unravel_index(np.argmin(distSq, axis=None), distSq.shape)
La función update_weights() tiene como inputs
mapa SOM
x: vector de entrenamiento (train_ex(ample))los parámetros
tasa de aprendizaje
radio del kernel
coordenadas de la BMU en el grid
parámetro
steprelacionado con el máximo número de celdas a actualizar en cualquier dirección
Esta función actualiza los valores de los vectores prototipos de las neuronas del mapa SOM.
Si el radio es cercano a cero, solamente actualiza la neurona BMU. En caso contrario, actualiza solamente las celdas en un vecindario de la BMU dado por step.
def update_weights(SOM, train_ex, learn_rate, radius_sq,
BMU_coord, step=3):
g, h = BMU_coord
if radius_sq < 1e-3:
SOM[g,h,:] += learn_rate * (train_ex - SOM[g,h,:])
return SOM
for i in range(max(0, g-step), min(SOM.shape[0], g+step)):
for j in range(max(0, h-step), min(SOM.shape[1], h+step)):
dist_sq = np.square(i - g) + np.square(j - h)
dist_func = np.exp(-dist_sq / 2 / radius_sq)
SOM[i,j,:] += learn_rate * dist_func * (train_ex - SOM[i,j,:])
return SOM
La función train_SOM realiza el entrenamiento de la red neuronal. Requiere
SOM inicializado o parcialmente entrenado
Es posible tener un mapa SOM parcialmente entrenado y guardar el resultado
datos de entrenamiento,
xlos parámetros de aprendizaje:
tasa de aprendizaje
decay de aprendizaje
radio del kernel
decay del radio
número de epochs de aprendizaje
def train_SOM(SOM, train_data, learn_rate = .1, radius_sq = 1,
lr_decay = .1, radius_decay = .1, epochs = 10):
learn_rate_0 = learn_rate
radius_0 = radius_sq
for epoch in np.arange(0, epochs):
rand.shuffle(train_data)
for train_ex in train_data:
g, h = find_BMU(SOM, train_ex)
SOM = update_weights(SOM, train_ex,
learn_rate, radius_sq, (g,h))
learn_rate = learn_rate_0 * np.exp(-epoch * lr_decay)
radius_sq = radius_0 * np.exp(-epoch * radius_decay)
return SOM
Datos de entrenamiento¶
Fabricamos un ejemplo para usar el SOM
Inicializamos un conjunto de \(n_x=3000\) datos de tipo RGB, es decir, tuplas de tres números enteros en el rango \([0,255]\). Cada uno de ellos lo podemos representar como un pixel coloreado con la función imshow del paquete pyplot.
n_x = 3000
rand = np.random.RandomState(0)
train_data = rand.randint(0, 255, (n_x, 3))
train_data.shape,train_data[0]
((3000, 3), array([172, 47, 117]))
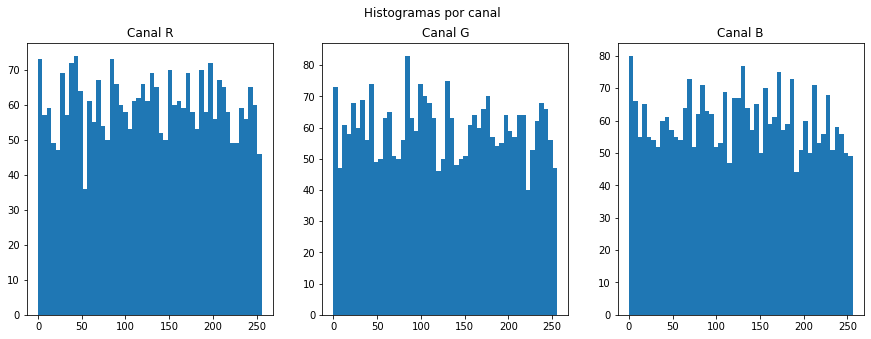
Histogramas de la distribución de cada canal¶
f,ax=plt.subplots(nrows=1,ncols=3,figsize=(15,5))
bins = 50
ax[0].hist(train_data[:][:,0],bins=bins,range=(0,256))
ax[0].set_title('Canal R')
ax[1].hist(train_data[:][:,1],bins=bins,range=(0,256))
ax[1].set_title('Canal G')
ax[2].hist(train_data[:][:,2],bins=bins,range=(0,256))
ax[2].set_title('Canal B')
f.suptitle('Histogramas por canal')
plt.plot()
[]
train_data[0:10]
array([[172, 47, 117],
[192, 67, 251],
[195, 103, 9],
[211, 21, 242],
[ 36, 87, 70],
[216, 88, 140],
[ 58, 193, 230],
[ 39, 87, 174],
[ 88, 81, 165],
[ 25, 77, 72]])
Representamos los diez primeros datos usando la función imshow
f,ax = plt.subplots(nrows=1,ncols=1,figsize=(4,4))
ax.imshow(train_data[0:10].reshape(2,5,3))
<matplotlib.image.AxesImage at 0x7f6ee0176d60>

Representamos todos los datos iniciales
fig, ax = plt.subplots(
nrows=1, ncols=1, figsize=(12, 12),
subplot_kw=dict(xticks=[], yticks=[]))
ax.imshow(train_data.reshape(50, 60, 3))
ax.title.set_text('Training Data')

Creamos una red SOM y la inicializamos¶
La red tiene un tamaño de \(10\times 10\) nodos en un mallado bidimensional rectangular.
Inicializamos los 100 vectores con valores aleatorios en los tres atributos (R,G,B).
Mostramos dos inicializaciones diferentes.
# Dimensiones
m = 10
n = 10
f,ax=plt.subplots(nrows=1,ncols=2,figsize=(10,5))
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
ax[0].imshow(SOM.astype('int'))
ax[0].set_title('Inicialización aleatoria 1')
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
ax[1].imshow(SOM.astype('int'))
ax[1].set_title('Inicialización aleatoria 2')
f.suptitle('SOM inicial')
plt.plot()
[]
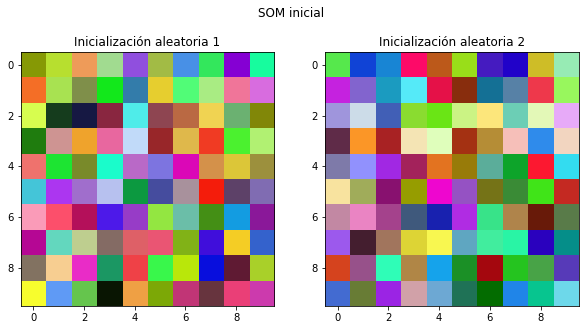
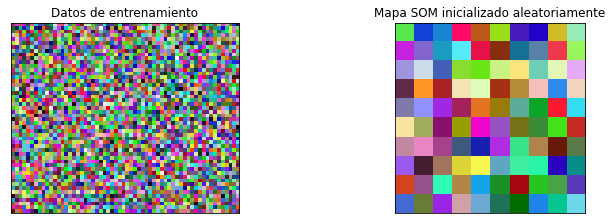
fig, ax = plt.subplots(
nrows=1, ncols=2, figsize=(12, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
ax[0].imshow(train_data.reshape(50, 60, 3))
ax[0].title.set_text('Datos de entrenamiento')
ax[1].imshow(SOM.astype(int))
ax[1].title.set_text('Mapa SOM inicializado aleatoriamente')
Entrenamiento del SOM¶
Visualizamos cómo evoluciona el mapa SOM en diferentes epochs de aprendizaje
fig, ax = plt.subplots(
nrows=1, ncols=4, figsize=(15, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
total_epochs = 0
for epochs, i in zip([1, 4, 5, 10], range(0,4)):
total_epochs += epochs
SOM = train_SOM(SOM, train_data, epochs=epochs)
ax[i].imshow(SOM.astype(int))
ax[i].title.set_text('Epochs = ' + str(total_epochs))
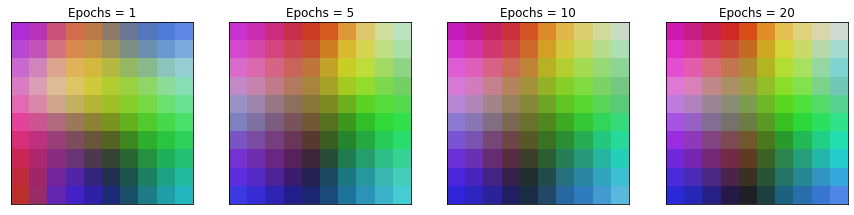
Efecto del tamaño del SOM¶
Usamos un grid de \(20\times20\) neuronas
Realizamos dos entrenamientos a partir de condiciones iniciales diferentes
m = 20
n = 20
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
fig, ax = plt.subplots(
nrows=1, ncols=4, figsize=(15, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
total_epochs = 0
for epochs, i in zip([1, 4, 5, 10], range(0,4)):
total_epochs += epochs
SOM = train_SOM(SOM, train_data, epochs=epochs)
ax[i].imshow(SOM.astype(int))
ax[i].title.set_text('Epochs = ' + str(total_epochs))
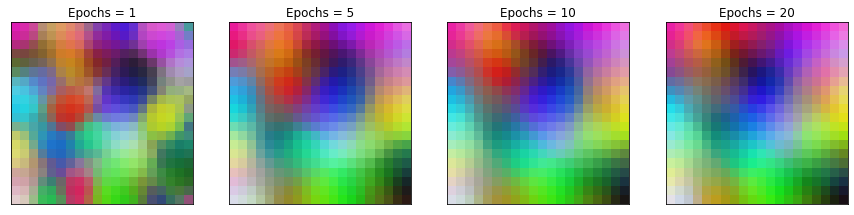
m = 20
n = 20
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
fig, ax = plt.subplots(
nrows=1, ncols=4, figsize=(15, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
total_epochs = 0
for epochs, i in zip([1, 4, 5, 10], range(0,4)):
total_epochs += epochs
SOM = train_SOM(SOM, train_data, epochs=epochs)
ax[i].imshow(SOM.astype(int))
ax[i].title.set_text('Epochs = ' + str(total_epochs))
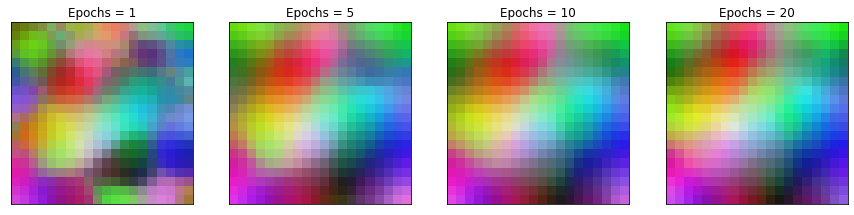
Important
No estamos convergiendo al mismo mapa, pero en ambos casos convergemos a un mapa que preserva las propiedades topológicas del espacio de datos de entrada.
Comparamos las distribuciones de los canales de color en los datos de entrenamiento y en el SOM entrenado.
f,ax=plt.subplots(nrows=2,ncols=3,figsize=(15,10))
bins = 20
ax[0,0].hist(train_data[:,0],bins=bins,range=(0,256))
ax[0,0].set_title('Datos Canal R')
ax[0,1].hist(train_data[:,1],bins=bins,range=(0,256))
ax[0,1].set_title('Datos Canal G')
ax[0,2].hist(train_data[:,2],bins=bins,range=(0,256))
ax[0,2].set_title('Datos Canal B')
bins = 20
ax[1,0].hist(SOM.reshape(m*n,3)[:,0],bins=bins,range=(0,256))
ax[1,0].set_title('SOM Canal R')
ax[1,1].hist(SOM.reshape(m*n,3)[:,1],bins=bins,range=(0,256))
ax[1,1].set_title('SOM Canal G')
ax[1,2].hist(SOM.reshape(m*n,3)[:,2],bins=bins,range=(0,256))
ax[1,2].set_title('SOM Canal B')
Text(0.5, 1.0, 'SOM Canal B')
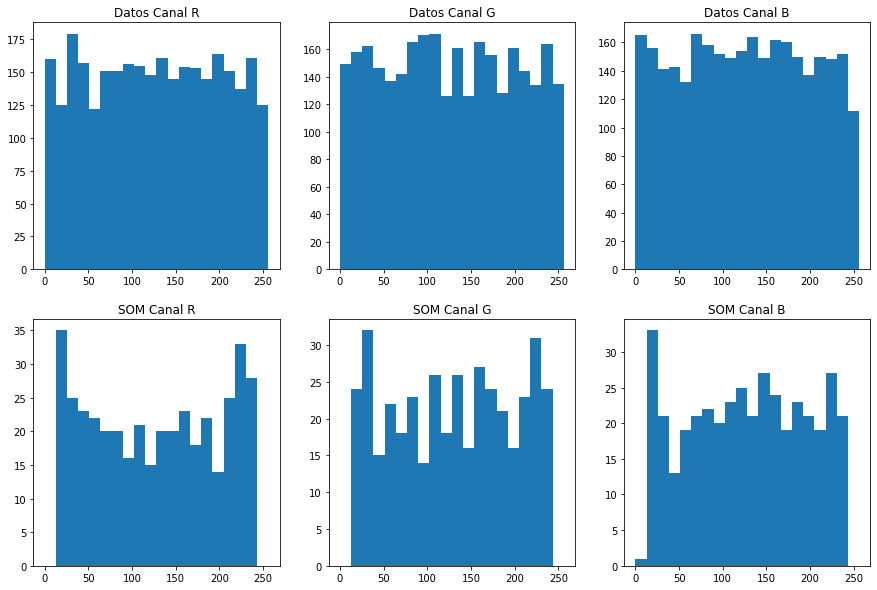
Datos iniciales con sesgo¶
Realizamos la misma prueba con datos iniciales sesgados hacia el rojo.
n_x = 3000
rand = np.random.RandomState(0)
train_data_R = rand.randint(175, 255, (n_x, 1))
train_data_G = rand.randint(0, 200, (n_x, 1))
train_data_B = rand.randint(0, 150, (n_x, 1))
train_data = np.zeros((n_x,3)).astype('int')
train_data[:,0] = train_data_R.reshape(n_x,)
train_data[:,1] = train_data_G.reshape(n_x,)
train_data[:,2] = train_data_B.reshape(n_x,)
# inicializamos el SOM
m = 20
n = 20
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
SOMuntrained = SOM.copy()
# entrenamos el SOM
total_epochs = 0
for epochs, i in zip([1, 4, 5, 10], range(0,4)):
total_epochs += epochs
SOM = train_SOM(SOM, train_data, epochs=epochs)
#ax[i].imshow(SOM.astype(int))
#ax[i].title.set_text('Epochs = ' + str(total_epochs))
train_data[:10]
array([[201, 109, 145],
[184, 87, 37],
[247, 33, 11],
[176, 114, 58],
[251, 146, 15],
[215, 95, 110],
[221, 85, 0],
[220, 16, 139],
[210, 112, 122],
[192, 189, 35]])
fig, ax = plt.subplots(
nrows=1, ncols=3, figsize=(12, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
ax[0].imshow(train_data.reshape(50, 60, 3))
ax[0].title.set_text('Training Data')
ax[1].imshow(SOMuntrained.astype(int))
ax[1].title.set_text('Untrained SOM Grid')
ax[2].imshow(SOM.astype(int))
ax[2].title.set_text('Trained SOM Grid')

train_data[0:10,2]
array([145, 37, 11, 58, 15, 110, 0, 139, 122, 35])
# representamos los histogramas
bins = 20
f,ax=plt.subplots(nrows=3,ncols=3,figsize=(15,15))
ax[0,0].hist(train_data[:,0],bins=bins,range=(0,256))
ax[0,0].set_title('Datos Canal R')
ax[0,1].hist(train_data[:,1],bins=bins,range=(0,256))
ax[0,1].set_title('Datos Canal G')
ax[0,2].hist(train_data[:,2],bins=bins,range=(0,256))
ax[0,2].set_title('Datos Canal B')
ax[1,0].hist(SOMuntrained.reshape(m*n,3)[:,0],bins=bins,range=(0,256))
ax[1,0].set_title('SOM Untrained Canal R')
ax[1,1].hist(SOMuntrained.reshape(m*n,3)[:,1],bins=bins,range=(0,256))
ax[1,1].set_title('SOM Untrained Canal G')
ax[1,2].hist(SOMuntrained.reshape(m*n,3)[:,2],bins=bins,range=(0,256))
ax[1,2].set_title('SOM Unrtained Canal B')
ax[2,0].hist(SOM.reshape(m*n,3)[:,0],bins=bins,range=(0,256))
ax[2,0].set_title('SOM Canal R')
ax[2,1].hist(SOM.reshape(m*n,3)[:,1],bins=bins,range=(0,256))
ax[2,1].set_title('SOM Canal G')
ax[2,2].hist(SOM.reshape(m*n,3)[:,2],bins=bins,range=(0,256))
ax[2,2].set_title('SOM Canal B')
Text(0.5, 1.0, 'SOM Canal B')
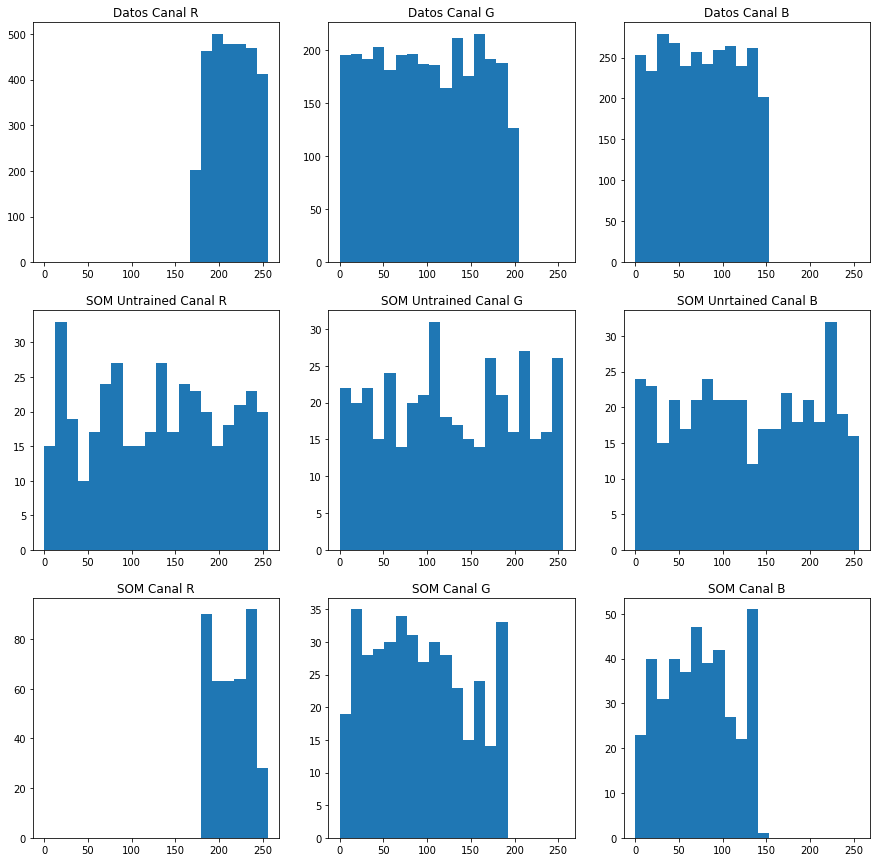
Efecto de los parámetros¶
Investigamos ahora el efecto que tienen los parámetros.
Realizamos gráficas de un SOM entrenado con un mallado de opciones para:
la tasa de aprendizaje
el radio del kernel de vecindad
Para radios cercanos a cero (primera columna) el algoritmo de aprendizaje solamente cambia las celdas individuales, pero no las vecinas. No se crea un mapa donde exista el fenómeno de emergencia, independientemente del valor de la tasa de aprendizaje.
La tasa de aprendizaje marca la velocidad con la que el SOM puede alcanzar la convergencia. Una alta tasa de aprendizaje realiza cambios más bruscos en los vectores, creando más ruido, mientras que una baja tasa de aprendizaje realiza cambios más sutiles, pero son necesarias muchas iteraciones para llegar a converger.
Importante: La correcta elección de los parámetros depende del caso de estudio.
m = 10
n = 10
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
n_x = 3000
rand = np.random.RandomState(75)
train_data = rand.randint(0, 255, (n_x, 3))
fig, ax = plt.subplots(
nrows=3, ncols=3, figsize=(15, 15),
subplot_kw=dict(xticks=[], yticks=[]))
for learn_rate, i in zip([0.001, 0.5, 0.99], [0, 1, 2]):
for radius_sq, j in zip([0.01, 1, 10], [0, 1, 2]):
rand = np.random.RandomState(0)
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
SOM = train_SOM(SOM, train_data, epochs = 5,
learn_rate = learn_rate,
radius_sq = radius_sq)
ax[i][j].imshow(SOM.astype(int))
ax[i][j].title.set_text('$\eta$ = ' + str(learn_rate) +
', $\sigma^2$ = ' + str(radius_sq))

