4.1 Ejemplo inicial de cadena de Markov¶

El tiempo en mi ciudad¶

En cierta ciudad se sabe que tres de cada cinco dı́as llueve si ha llovido el dı́a anterior, y cuatro de cada cinco dı́as está soleado si el dı́a anterior fue soleado.

Hoy llueve en la ciudad.

Un hombre de allı́ nos pregunta por la probabilidad de que, después de un mes, aparezca un dı́a soleado o uno lluvioso.

¿Sabrías contestarle?

Estudiamos el problema¶

Notación¶

Llamamos \(L_n\) al suceso ‘’el día \(n\) es lluvioso’’
\(S_n\) ‘’el día \(n\) es soleado’’

Entonces:

La probabilidad de pasar de lluvioso (el día \(n\)) a lluvioso (\(n+1\)) es:

\[ p_{L\rightarrow L}=\mathbb{P}\{L_n\rightarrow L_{n+1}\}=\frac{3}{5} \]

La probabilidad de pasar de soleado (el día \(n\)) a soleado (\(n+1\)) es:

\[ p_{S\rightarrow S}=\mathbb{P}\{S_n\rightarrow S_{n+1}\}=\frac{4}{5} \]

Transiciones entre estados¶

Hay otros dos posibles sucesos: \(L_n\rightarrow S_{n+1}\) y \(S_{n}\rightarrow L_{n+1}\)

¿Qué probabilidad tiene cada uno de estos sucesos?

Podemos representar las transiciones entre estados mediante una red dirigida de transiciones en la que hay ciertos pesos en cada uno de los enlaces.

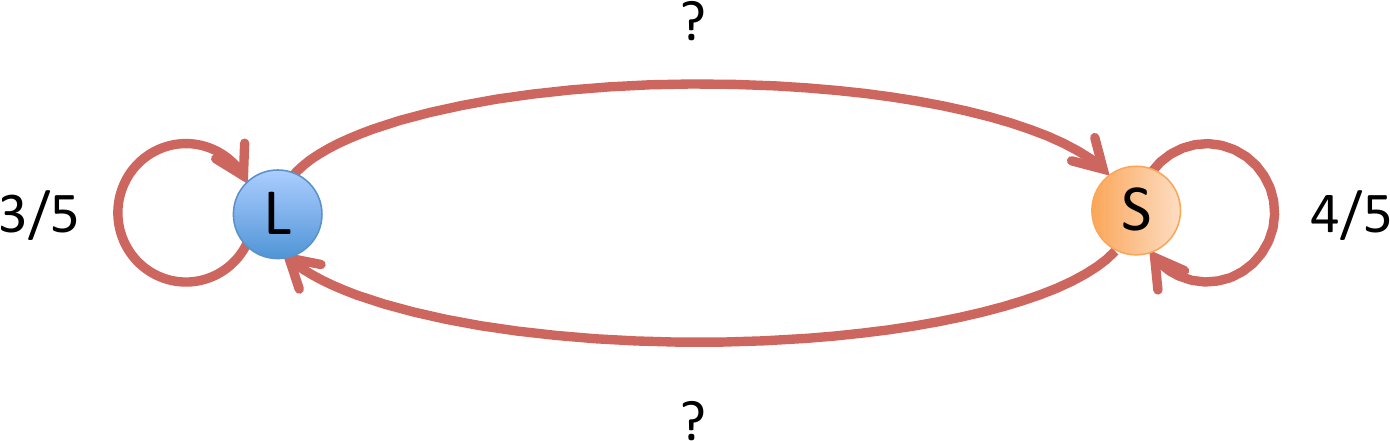
Fig. 3 Transiciones entre estados¶

Los pesos (probabilidades) de las transiciones son:

\[ p_{L\rightarrow S}=1-p_{L\rightarrow L},\qquad p_{S\rightarrow L}=1-p_{S\rightarrow S} \]

ya que:

Dos de cada cinco dı́as el dı́a siguiente a uno lluvioso es soleado.
Uno de cada cinco dı́as el dı́a siguiente a uno soleado es lluvioso.

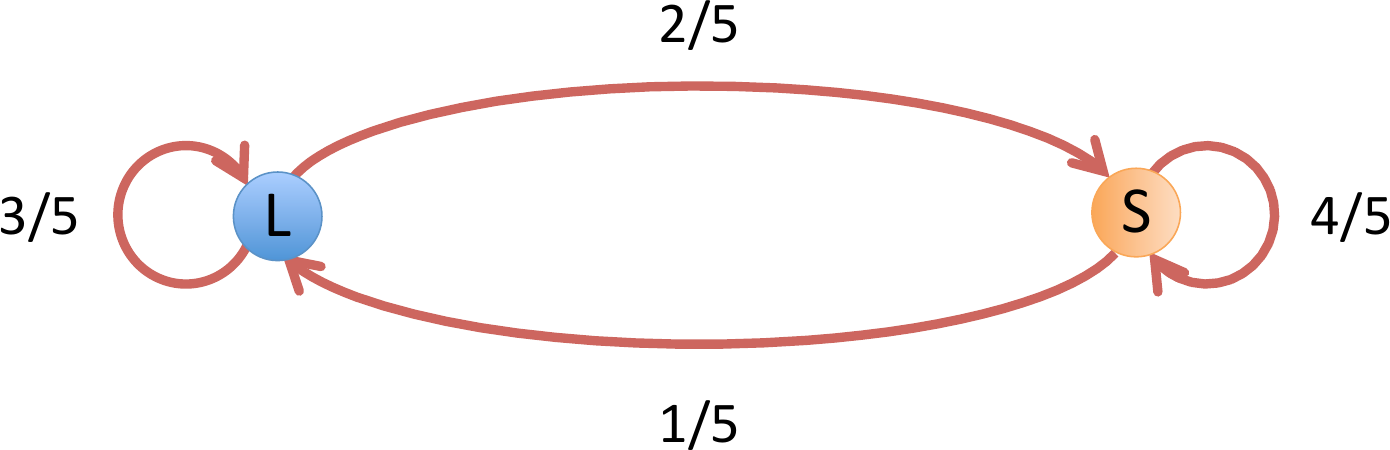
Fig. 4 Transiciones entre estados¶

Matriz de transiciones¶

Formamos la siguiente matriz con las probabilidades de transición:

\[\begin{split} P= \begin{matrix} {\color{red}L}\\{\color{red}S} \end{matrix} \stackrel{L\quad S}{ \begin{pmatrix} p_{{\color{red}L}\rightarrow L} & p_{{\color{red}L}\rightarrow S} \\ p_{{\color{red}S}\rightarrow L} & p_{{\color{red}S}\rightarrow S} \end{pmatrix} } =\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix} \end{split}\]

Las filas de esta matriz suman 1.

Probabilidades a un paso¶

Si partimos de la condición inicial de que el dı́a de hoy llueve, las probabilidades asociadas a cada estado (lluvioso, soleado) a tiempo cero son:

\[ \mathbf{\pi}^{(0)}=\left( \mathbb{P}\{L_0\},\quad\mathbb{P}\{S_0\} \right)=(1,0). \]

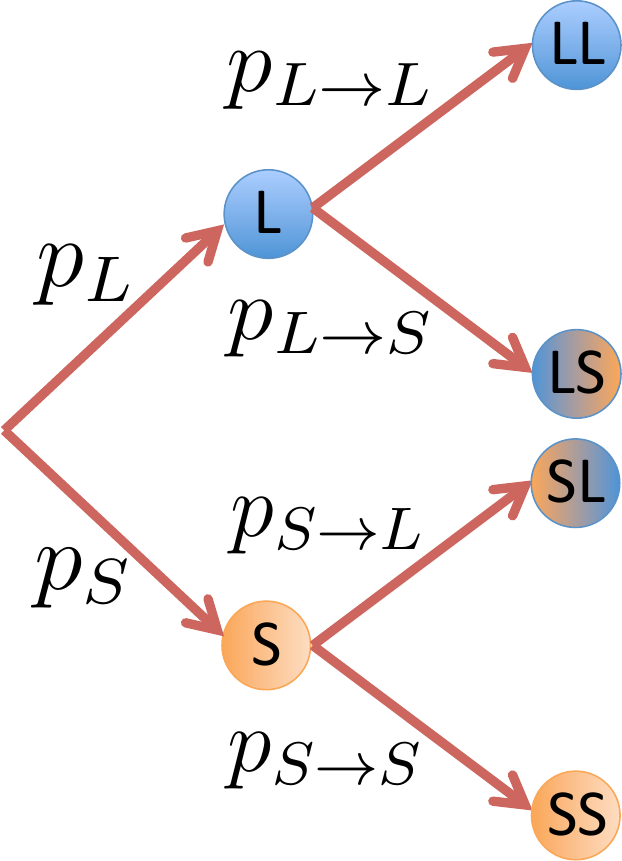
Fig. 5 Transiciones y probabilidades¶

Por el Teorema de la Probabilidad Total,

\[\mathbb{P}\{ {\color{blue}L}_1 \} = \mathbb{P} \{ {\color{red}L}_0 \} \cdot p_{ {\color{red}L} \rightarrow {\color{blue}L} }+ \mathbb{P}\{ {\color{red}S}_0 \}\cdot p_{{\color{red}S}\rightarrow {\color{blue}L}}. \]

y

\[ \mathbb{P}\{{\color{blue}S}_1\}=\mathbb{P}\{{\color{red}L}_0\}\cdot p_{{\color{red}L}\rightarrow {\color{blue}S}}+ \mathbb{P}\{{\color{red}S}_0\}\cdot p_{{\color{red}S}\rightarrow {\color{blue}S}}. \]

Es decir:

\[\begin{split} {\color{red}{\mathbf{\pi}^{(1)}}} = \left( \mathbb{P}\{L_1\},\quad \mathbb{P}\{S_1\} \right)= \left( \mathbb{P}\{L_0\},\quad \mathbb{P}\{S_0\} \right)\cdot \begin{pmatrix} p_{L\rightarrow L} & p_{L\rightarrow S} \\ p_{S\rightarrow L} & p_{S\rightarrow S}\end{pmatrix} = {\color{red}{\mathbf{\pi}^{(0)}P}} \end{split}\]

En nuestro ejemplo

\[\begin{split} \mathbf{\pi}^{\color{red}{(1)}} =(1,0)\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix}=\left(\frac{3}{5},\frac{2}{5}\right) \end{split}\]

Probabilidades a \(n\) pasos¶

A dos pasos tenemos

\[\begin{split} \mathbf{\pi}^{\color{red}{(2)}} = \mathbf{\pi}^{(1)}P = \mathbf{\pi}^{(0)}P^{\color{red}{2}} = (1, 0) \begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix}^{\color{red}{2}} = (0.44, \quad0.56) \end{split}\]

A tres pasos

\[\begin{split} \mathbf{\pi}^{\color{red}{(3)}} =\mathbf{\pi}^{(2)}P=\mathbf{\pi}^{(0)}P^{\color{red}{3}}=(1, 0)\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix}^{\color{red}{3}}=(0.376,\quad 0.624) \end{split}\]

Después de 30 pasos

\[\begin{split} \mathbf{\pi}^{\color{red}{(30)}}=(1, 0)\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix}^{\color{red}{30}}=(0.3333333,\quad 0.6666667) \end{split}\]

Observaciones:

La probabilidad de que llueva después de un mes es \(\frac{1}{3}\).
La probabilidad de que el día sea soleado es de \(\frac{2}{3}\).
Las componentes del vector \(\pi^{(n)}\) siempre suman 1.

Ejercicio: potencias de una matriz¶

¿Recuerdas cómo es la manera más efectiva de calcular las potencias de una matriz cuadrada?

¿Puedes calcular la potencia \(n\)-ésima de la matriz anterior con Python?

Introducción al Aprendizaje Automático