import numpy as np
import matplotlib.pyplot as plt
6.3 El Algoritmo SOM¶
Pasos del algoritmo¶
Pasos elementales del algoritmo básico (online) de generación de un mapa auto-organizativo a partir de un conjunto de datos:
Seleccionar tamaño y tipo (hexagonal, cuadrado) del mapa
Típicamente se prefieren grids hexagonales
Inicializar todos los vectores de pesos
Posiblemente de manera aleatoria, aunque existen variantes
Elegir un dato del conjunto de entrenamiento y enfrentarlo al SOM
(Competición) Encontrar la mejor neurona (Best Matching Unit, BMU) del mapa, e.g. la más similiar
Usualmente la más cercana de acuerdo con la métrica euclídea
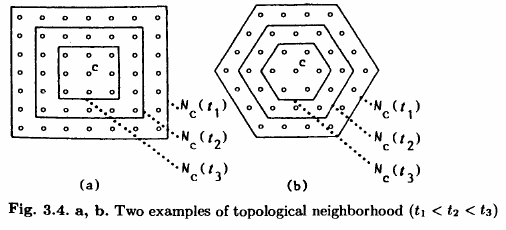
(Cooperación) Determinar las neuronas dentro del entorno de la BMU
Usualmente el tamaño del entorno decrece con la iteración
(Adaptación) Ajustar los pesos de las neuronas en el entorno de la BMU hacia el dato mostrado.
En general, la tasa de aprendizaje decrece con cada iteración
La magnitud del ajuste es proporcional a la proximidad de la neurona a la BMU
Repetir pasos 2-6 para \(N\) iteraciones hasta convergencia
Datos numéricos¶
Consideramos en caso discreto donde el espacio de entrada \(\mathcal{X}\) son \(N\) puntos de \(\mathbb{R}^d\)
Un conjunto finito de vectores con \(d\) componentes / atributos
Grid y entorno local¶
Las neuronas del mapa forman un mallado de \(L\) elementos, en una o dos dimensiones
También se puede realizar en dimensiones mayores
El mallado define la relación de vecindad de las neuronas
Vector asociado a las neuronas¶
A cada neurona se le asocia un vector (prototipo)
Es decir:
donde
\(d\): dimensión de las instancias (número de atributos)
\(L\): número de neuronas (unidades) de la red
Los valores iniciales de estos vectores se suelen asignar aleatoriamente (aunque existen otras técnicas). Estos vectores cambian con el tiempo (iteración) de aprendizaje, hasta formar el SOM.
El conjunto de todos los prototipos en un tiempo de aprendizaje / iteración \(t\):
Función de vecindad: núcleo de entorno¶
Dado \(\mathcal{L}=\{1,\ldots,L\}\) el conjunto de las neuronas, y \(t\) el tiempo (iteración de aprendizaje), se define una función
que satisface las siguientes propiedades:
\(h\) es simétrica
\(h_t(k,k)=1\) para todo \(k\in\mathcal{L}\)
\(h_t(k,l)\) depende únicamente de la distancia \(d(k,l)\) entre las neuronas \(k\) y \(l\) en el mallado
denotamos distancia \(d(k,l)=\|r_k-r_l\|\), y entonces
es monótona decreciente
Recordatorio: Distancia euclídea¶
La distancia euclídea entre dos puntos de \(\mathbb{R}^n\) es
Opciones de función de vecindad¶
Función meseta: es igual a 1 si la distancia entre \(k\) y \(l\) es menor que cierto radio (que puede ser función del tiempo), y 0 en otro caso
donde \(\rho(t)\) es una función decreciente con el tiempo.
Función gaussiana:
donde \(\alpha\) y \(\sigma\) son funciones decrecientes del tiempo.
Un ejemplo puede ser
Función recortada: si definimos un conjunto de puntos, \(N_c\subset\mathcal{L}\), que conforman el entorno de una neurona cualquiera \(c\in\mathcal{L}\) entonces:
donde \(\alpha(t)\) es una función monótona decreciente para todo \(t\) y \(0<\alpha(t)<1\).
Radio de influencia¶
El radio, \(\sigma\) determina el tamaño de la región de influencia del dato de entrenamiento \(x\). Una estrategia común es comenzar el aprendizaje con un radio grande e ir reduciéndolo a medida que avanzan las iteraciones.
donde \(\beta<0\) es la tasa de decaimiento.
Observación: usando un \(\sigma^2\leq 10\), el valor del kernel es casi cero para neuronas a distancia mayor o igual a 10.
Observaciones¶
Si la distancia de la neurona \((i,j)\) al BMU es grande, \(h_t\) tenderá a cero, realizándose en ese caso un cambio casi imperceptible en el vector prototipo de la neurona.
Los datos de aprendizaje afectan, por tanto, al BMU (en la mayor cantidad) y a las neuronas vecinas en cantidad decreciente con la distancia de éstas al BMU.
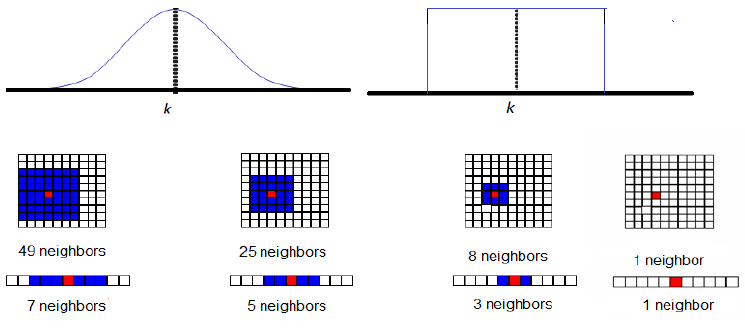
Fig. 33 Funciones vecindad e impacto en el mallado del SOM¶
distance = np.arange(0, 30)
sigma_sq = [0.1, 1, 10, 100]
fig,ax = plt.subplots(nrows=1, ncols=4, figsize=(15,4))
plt_ind = np.arange(4) + 141
for s, ind in zip(sigma_sq, plt_ind):
plt.subplot(ind)
f = np.exp(-distance ** 2 / 2 / s)
plt.plot(distance, f, c='cyan')
plt.title('$\sigma^2$ = ' + str(s))
plt.xlabel('Distance')
plt.ylabel('Neighborhood function $f$')
fig.subplots_adjust(hspace=0.5, wspace=0.3)
plt.show()
Competición¶
Elección de la Best Matching Unit¶
Supongamos:
paso \(t\) del aprendizaje
el vector de entrada es \(\mathbf{x}_i=(x_{i1},x_{i2},\ldots,x_{im})\)
Note
\(i\) no tiene que ser igual a \(t\) ¿por qué?
asociada a cada neurona \(j\in\mathcal{L}\) en el paso \(t\) está asociado el vector
Nota: si el mapa es bidimensional entonces \(\mathcal{L}=\mathcal{L}_1\times \mathcal{L}_2\) es el número total de neuronas dispuestas en el mapa bidimensional.
Best Matching Unit:¶
La neurona que mejor refleja la información recogida en el vector de entrada \(\mathbf{x}_i\) es la Best Matching Unit (BMU) y es la neurona que cumple que la distancia de su prototipo en el tiempo \(t\) al dato de entrada es mínima:
En la práctica se suele elegir la distancia euclídea:
Cooperación y Adaptación¶
Actualización de los vectores de referencia¶
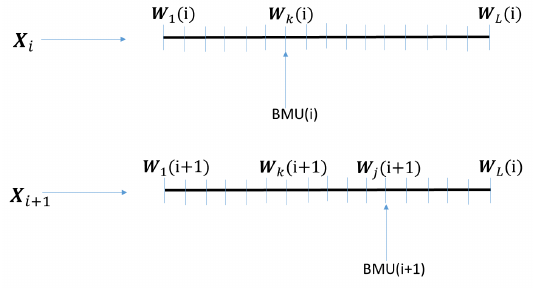
Fig. 34 Actualización de los vectores¶
Durante el proceso de entrenamiento, las neuronas cercanas a la que verifica la condición de máxima proximidad, \(BMU\), se actualizan:
donde
\(BMU\) es \(BMU_t(i)\)
\(\eta(t)\) es la tasa de aprendizaje (positiva, \(<1\), monótona decreciente)
\(h_t(BMU,k)\) es el núcleo de entorno (centrado en \(BMU_t(i)\))
\((\mathbf{x}_i-\mathbf{W}_k(t))\) es un vector cuyo origen está en \(\mathbf{W}_k(t)\) y extremo en \(\mathbf{x}\)
Note
Esto quiere decir que hay un \(\delta\in[0,1]\) tal que:
Pregunta: ¿Qué efecto geométrico está realizando esta operación? ¿Tiene algún efecto sobre la posición de las neuronas en el mapa?
Important
Si hemos definido un entorno \(N_c\) para cada neurona \(\mathbf{c}\in\mathcal{L}\) la actualización se realiza únicamente para las funciones de dicho entorno.
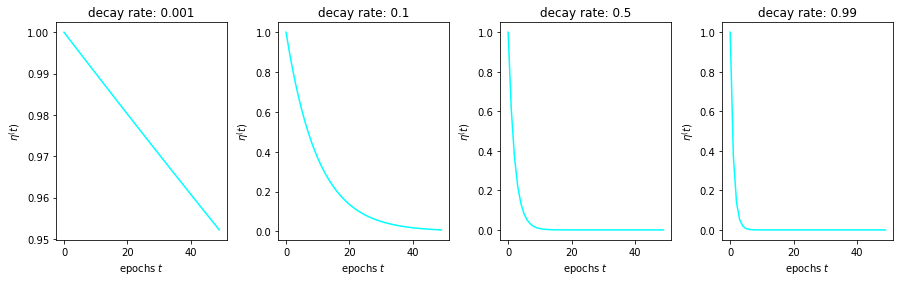
La tasa de aprendizaje¶
La tasa de aprendizaje escala la cantidad que se acerca el vector prototipo de la neurona al dato multidimensional que estamos considerando en la iteración.
Si \(\eta=0\) entonces no hay ningún cambio
Si \(\eta=1\) entonces el vector prototipo \(W_{k}(t+1)\) tomará el valor del dato \(x\)
Usualmente se considera una función \(\eta\) decreciente con el tiempo de aprendizaje (iteraciones, épocas del algoritmo). Una posible representación funcional de este comportamiento es:
donde \(\lambda<0\) es la tasa de decaimiento.
epochs = np.arange(0, 50)
lr_decay = [0.001, 0.1, 0.5, 0.99]
fig,ax = plt.subplots(nrows=1, ncols=4, figsize=(15,4))
plt_ind = np.arange(4) + 141
for decay, ind in zip(lr_decay, plt_ind):
plt.subplot(ind)
learn_rate = np.exp(-epochs * decay)
plt.plot(epochs, learn_rate, c='cyan')
plt.title('decay rate: ' + str(decay))
plt.xlabel('epochs $t$')
plt.ylabel('$\eta^(t)$')
fig.subplots_adjust(hspace=0.5, wspace=0.3)
plt.show()
Resultado¶
Obtenemos una partición del espacio de los datos llamada teselación de Voronoi
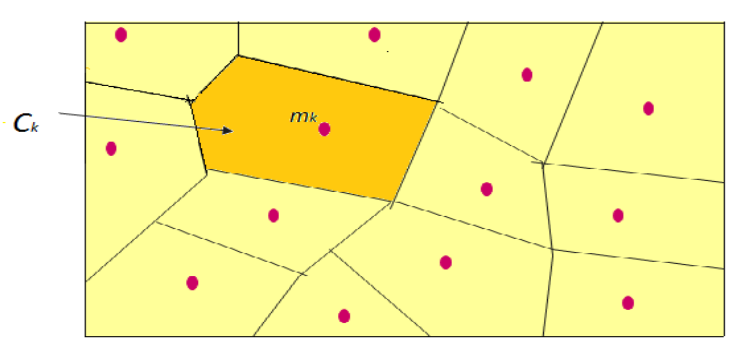
Fig. 35 Clusters en un SOM¶
Al terminar el aprendizaje se obtiene un SOM donde el efecto de la transformación puede hacer aparecer clusters asociados a las neuronas
Un cluster \(C_k\) se define como el conjunto de los inputs (datos de entrada) que son más cercanos a \(\mathbf{W}_k(\infty)\) que a cualquier otro \(\mathbf{W}_j(\infty)\), \(j\neq k\).
Existe una estructura de vecindad (una topología) entre los clusters
Visualizaciones¶
El mapa de Kohonen consiste en, o bien la representación de los prototipos (vectores asociados a las neuronas), o de los contenidos de cada cluster de acuerdo a la estructura de vecindad (posición en el lattice) de las neuronas.
Propiedades¶
Los prototipos del SOM representan el espacio de los datos de entrada fielmente, como hacen otros algoritmos de clustering
Auto-organización: los prototipos preservan la topología de los datos: inputs cercanos estarán o bien en el mismo cluster (como hacen otros algoritmos de clustering) o en clusters cercanos
Convergencia¶
El algoritmo es fácil de programar y usar, y muchos estudios prácticos confirman que funciona.
No obstante, el problema de la convergencia en algoritmos no supervisados no es inmediata.
Cuando \(t\to\infty\) el proceso estocástico
en \(\mathbb{R}^d\) puede presentar
oscilaciones
explotar al infinito
convergencia (en distribución) a un proceso de equilibrio
convergencia (en distribución o casi seguro) a un conjunto finito de puntos en \(\mathbb{R}^d\)
De hecho, en el caso de SOM bidimensionales no existe una prueba completa y el problema permanece abierto.
En el caso de SOM unidimensionales hay resultados más completos
Preguntas abiertas¶
¿Es el algoritmo convergente en distribución o casi seguro cuando \(t\to\infty\)?
¿Cuál es el efecto de \(\eta(t)\)?
Si existe un estado límite, ¿es estable?
¿Cómo caracterizamos la organización?
Cuantificación del error¶
Una manera de medir la convergencia hacia una organización óptima es mediante una función error.
En el caso discreto, se puede probar que
donde
\(BMU=BMU(x_i)\) (elegida según el algoritmo descrito más arriba)
\(N\) es el número total de datos de entrada
es una función de energía o, también denominada, distorsión.
Esta función combina dos criterios:
un criterio de clustering
un criterio de organización correcta
No obstante, la existencia de esta función energía no asegura la convergencia
el gradiente de la función no es continua en los bordes de los clusters
Para minimizar este error se realizan varios entrenamientos con diferentes condiciones iniciales
se elige el mapa con el menor error
Otras versiones del SOM¶
SOM Determinista Batch
Existe una versión determinista del SOM, para obtener resultados reproducibles cuando los los valores iniciales de los prototipos son fijos.
En esta versión se usan todos los datos en cada iteración.
SOM para datos no numéricos
Existen versiones del SOM para datos no numéricos
Pseudocódigo¶
Stochastic learning¶
foreach \(\mathbf{w}_i\in\mathbf{W}\):
Initialize \(w_i\)
while _stopping condition(s) not true:
Select random input vector \(\mathbf{x}_i\in\mathbf{X}\)
Find the best mathching neuron (BMU) for \(\mathbf{x}_i\)
foreach \(\mathbf{w}_i\in\mathbf{W}\):
Update \(\mathbf{w}_i\)
end for
end
Batch learning¶
foreach \(\mathbf{w}_i\in\mathbf{W}\):
Initialize \(w_i\)
while _stopping condition(s) not true:
foreach \(\mathbf{w}_i\in\mathbf{W}\):
\(X_i\leftarrow\emptyset\)
foreach \(\mathbf{x}_i\in\mathbf{X}\):
if \(\mathbf{x}_i\) is in neighbourhood of \(\mathbf{w}_i\):
Add \(\mathbf{x}_i\) to \(X_i\)
end if
end for
end for
foreach \(\mathbf{w}_i\in\mathbf{W}\):
\(\mathbf{w}_i\leftarrow\) update mean over \(X_i\)
end for
end
Bioinspirado¶
Existe una ingente cantidad de experimentos y observaciones que demuestran la existencia de un orden espacial en la organización de las funciones cerebrales.
Ubicuo en los sistemas nerviosos
Implantado en los modelos de redes neuronales?
Compartimentalización del cerebro en partes macroscópicas (no necesariamente anatómicas) con funciones concretas
nuclei que controlan la emoción, arousal, intención
existe una organización espacial en el tejido cerebral en el que observa una correlación entre funciones neuronales y coordenadas del área cerebral
hay areas asociativas en las cuales las señales de diferente modalidad convergen
La posibilidad de que la representación del conocimiento de una particular categoría de cosas pueda asumir la forma de un mapa de características que está geométricamente organizado sobre un trozo correspondiente de cerebro motivó a Kohonen para crear los SOM.
Kohonen pretende crear un mecanismo de aprendizaje que crease mapas globalmente ordenados de diferentes inputs sensoriales en una red neuronal con capas.
En la fase de aprendizaje
inputs recibidos por la experiencia práctica, sin supervisión
los inputs controlan las conexiones neuronales: se refuerzan o desaparecen
Modeliza la plasticidad de las conexiones sinápticas en el cerebro.
La selección de vector del codebook más próximo, llamado ganador o BMU no está basada en una comparación métrica directa, si no en un mecanismo de interacción colectiva, que se observa en networks interconectadas similares a las del cerébro.
El proceso se denomina competitive learning
en neurociencia se suele hablar de competición entre los elementos cuando son estimulados por el mismo input, y el elemento, cuyos parámetros se ajustan más al input es el más activado
si el elemento más activado suprime la actividad de las neuronas adyacentes, se le conoce como winner
si el proceso se repite aparece una estructura en la organización de las neuronas: emergen mapas que están relacionados topológicamente a los inputs sensoriales (signal space)
En las redes en las que se da el competitive learning, las células reciben el mismo input de información, sobre el cual compiten.
un mensaje entrante \(X\) se compara con todos los posibles modelos \(M_i\)
Mediante interacciones laterales (positivas y negativas), una de las células se convierte en la ganadora (y suprime la actividad de todas las demás células con un feedback negativo).
emergencia de feature-specific-cells_: neuronas (o sistemas de neuronas) que responden de manera selectiva a input patterns
las celdas o unidades no se mueven a ninguna parte: el conjunto de sus parámetros internos es el que cambia y define la especificidad de cada celda
Como las networks son usualmente planas, entonces obtenemos funciones que mapean el espacio de los inputs, preservando las relaciones topológicas y reduciendo la dimensión.