6.2 Mapas autoorganizativos¶
Ejemplo paradigmático de algoritmo de aprendizaje no supervisado bio-inspirado capaz de agrupar datos
Propiedades¶
Los mapas autoorganizativos:
Son un algoritmo de aprendizaje no supervisado
Tienen aplicación tanto en el campo del clustering como en la clasificación
También se puede aplicar como una herramienta de clasificación con aprendizaje supervisado
Producen una representación en usualmente dos dimensiones de los inputs
Datos multidimensionales son representados en mapas bi-dimensionales de nodos
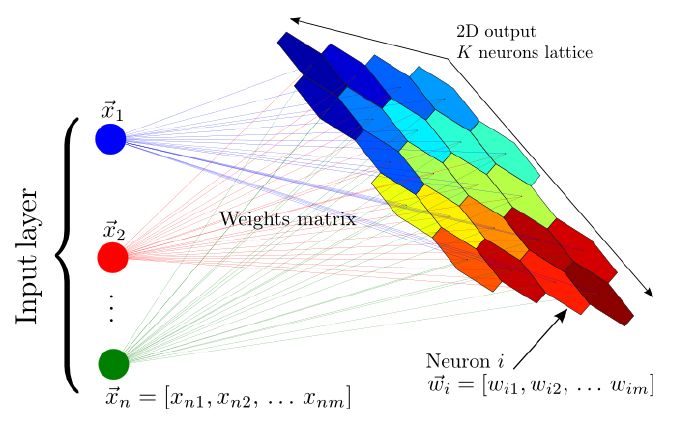
Fig. 27 Ejemplo de mapa- SOM¶
El tiempo de computación aumenta linealmente con el tamaño de los datos.
Tienen una complejidad lineal por lo que son adecuados para problemas de Big Data
Red Neuronal del SOM¶
El SOM es una red neuronal formada por un grid (usualmente bidimensional) de nodos/neuronas
Mediante entrenamiento la red es capaz de aprender a relacionar topográficamente los vectores de entrada con los vectores de la red (neuronas).
Los SOM son mapas que relacionan una señal de entrada con neuronas de una red de acuerdo con su proximidad topográfica
Impulsos similares son procesados por neuronas cercanas
Nodos / Neuronas¶
Cada nodo tiene una posición fija en el gráfico/grid
Cada nodo tiene asociado un vector prototípico de igual dimensión a la de los inputs (datos de entrada).
Por ejemplo, si usamos datos que contengan los campos/atributos “edad”, “sexo”, “altura”, “peso”, cada nodo del grid tendrá asociados unos valores para cada uno de los atributos
Cada neurona de la red (bidimensional) representa un vector de dimensión \(n>>2\)
(Una vez entrenado el SOM) cada nodo tiene asociado un subconjunto (puede ser vacío) de instancias de los datos de entrada
Cada instancia de los datos de entrada está linkeada a un nodo del mapa SOM
Son disjuntos 2 a 2
Un nodo puede representar varias instancias de los datos de entrada
Propiedades topológicas¶
La característica clave de un SOM es que las propiedades topológicas de los datos de entrada se preservan en en el mapa
Inputs cercanos (la similaridad se define en función de los atributos, e.g., edad, sexo,…) estarán representadas por nodos (neuronas) cercanas en el grid SOM.
Es un algoritmo de clustering que considera una estructura topológica (de vecindad) sobre los clusters
Los datos que están próximos pertenecerán al mismo clúster (al igual que otros algoritmos de clustering), o a clusters vecinos
Son una herramienta adecuada para la visualización de datos multidimensionales ya que los clústeres pueden ser representados de acuerdo a su topología (vecindad)

Fig. 28 Ejemplo de mapa- SOM¶
Visualización¶
Se utilizan para agrupar y representar conjuntos de datos de dimensiones elevadas en una red
habitualmente, bidimensional
también se utilizan redes 1D y 3D.
Una representación típica de un SOM es un heatmap que muestral la distribución de un atributo a través del mapa.
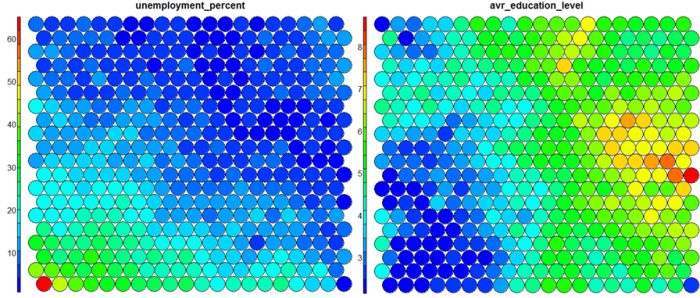
Fig. 29 SOM unidimensional¶
¿Qué opinas de este ejemplo?
Coges a todos los asistentes a un concierto. Les dices que comparen sus atributos (edad, género, salario, altura) y que se muevan hasta que están lo más cerca posible a otra gente cuyos atributos sean lo más similar a ellos. Si entonces cada uno muestra una carta al cielo indicando su atributo (edad), el resultado es un SOM heatmap.

Fig. 30 SOM unidimensional¶
Ayudan a hacer un análisis exploratorio de los datos
Realizan una reducción de la dimensionalidad de los datos
Bioinspirados¶
Son un caso concreto de redes neuronales en el cual es aprendizaje es competitivo
Basados en la interpretación de imágenes del sistema visual de los seres vivos
Plasticidad de las conexiones sinápticas del cerebro
Las conexiones neuronales se refuerzan o desaparecen en la fase de aprendizaje
Las modificaciones de las conexiones se hacen a través de la experiencia (inputs recibidos), sin supervisión
Desarrollo histórico¶
Diferentes variantes se han ido desarrollando hasta la fecha que permiten su aplicación a datos no numéricos (e.g. categóricos)
Presentación (1982):
Originalmente se utilizó para trabajar con valores númericos (versión on-line)
Una versión promedio (batch algorithm) fue presentada en
para trabajar con símbolos.
