03.3 Otros métodos de agrupación - Clustering Jerárquico y Densidad¶
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
import numpy as np
from skimage import io
from IPython import display
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
output_notebook()
En este cuaderno vamos a necesitar dibujar un dendograma¶
Se realiza, por ejemplo, con la siguiete función a medida:
import numpy as np
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram
from sklearn.datasets import load_iris
from sklearn.cluster import AgglomerativeClustering
def plot_dendrogram(model, **kwargs):
# Create linkage matrix and then plot the dendrogram
# create the counts of samples under each node
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack([model.children_, model.distances_,
counts]).astype(float)
# Plot the corresponding dendrogram
dendrogram(linkage_matrix, **kwargs)
Descripción general del método de agrupación jerárquica¶
A diferencia de K-means, son métodos deterministas.
Parten de una matriz \(D = (d_{ij})\) de distancias o \(S = (s_{ij})\) de similitudes, matrices \(N \times N\) entre los \(N\) elementos del conjunto de instancias.
Si todas las variables son continuas, la distancia más utilizada es la euclídea (con variables estandarizadas univariantemente en caso de ser conveniente).
Si hay variables continuas y categóricas no suele ser aceptable trabajar con distancias y se usan similitudes.
El algoritmo tiene los siguientes pasos:
Comenzamos con N grupos (uno para cada instancia) y la matriz D o S.
Buscamos los elementos más próximos (mínimo valor \(d_{ij}\) o \(s_{ij}\)) y los unimos en un grupo.
Recalculamos la matriz de distancias (o similitudes) definiendo una distancia o similitud entre este nuevo grupo y el resto.
Repetimos los dos pasos anteriores hasta que todas las observaciones estén unidas en un solo grupo
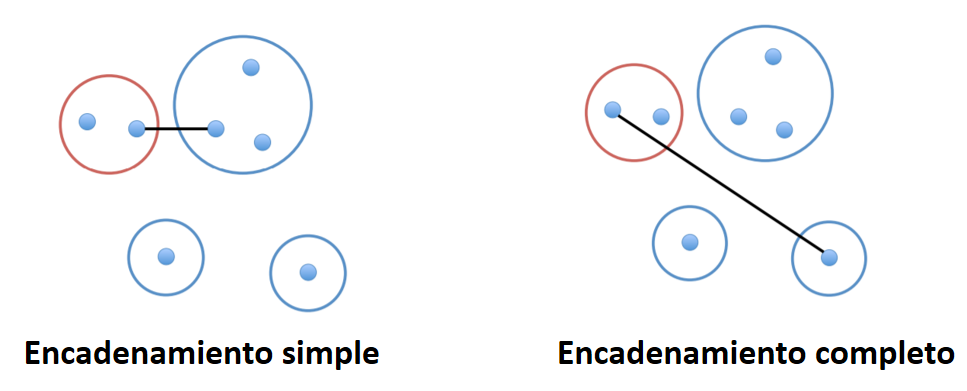
La forma de calcular la distancia entre grupos de puntos puede hacerse de diferentes formas como:
Por encadenamiento simple tomando como distancia de 2 grupos la de los 2 puntos más próximos. Tiende a encadenar individuos sueltos y no grupos.
Por encadenamiento completo tomando como distancia de 2 grupos la de los 2 puntos más alejados. Es menos sensible a atípicos.
Método de Ward que maximiza la homogeneidad intra-grupo. Como medida de homogeneidad se usa la suma de cuadrados de los errores. Tiende a formar grupos esféricos aunque los grupos no lo sean.
Una forma de visualizar la estructura del grupo gerárquico es con el dendograma.
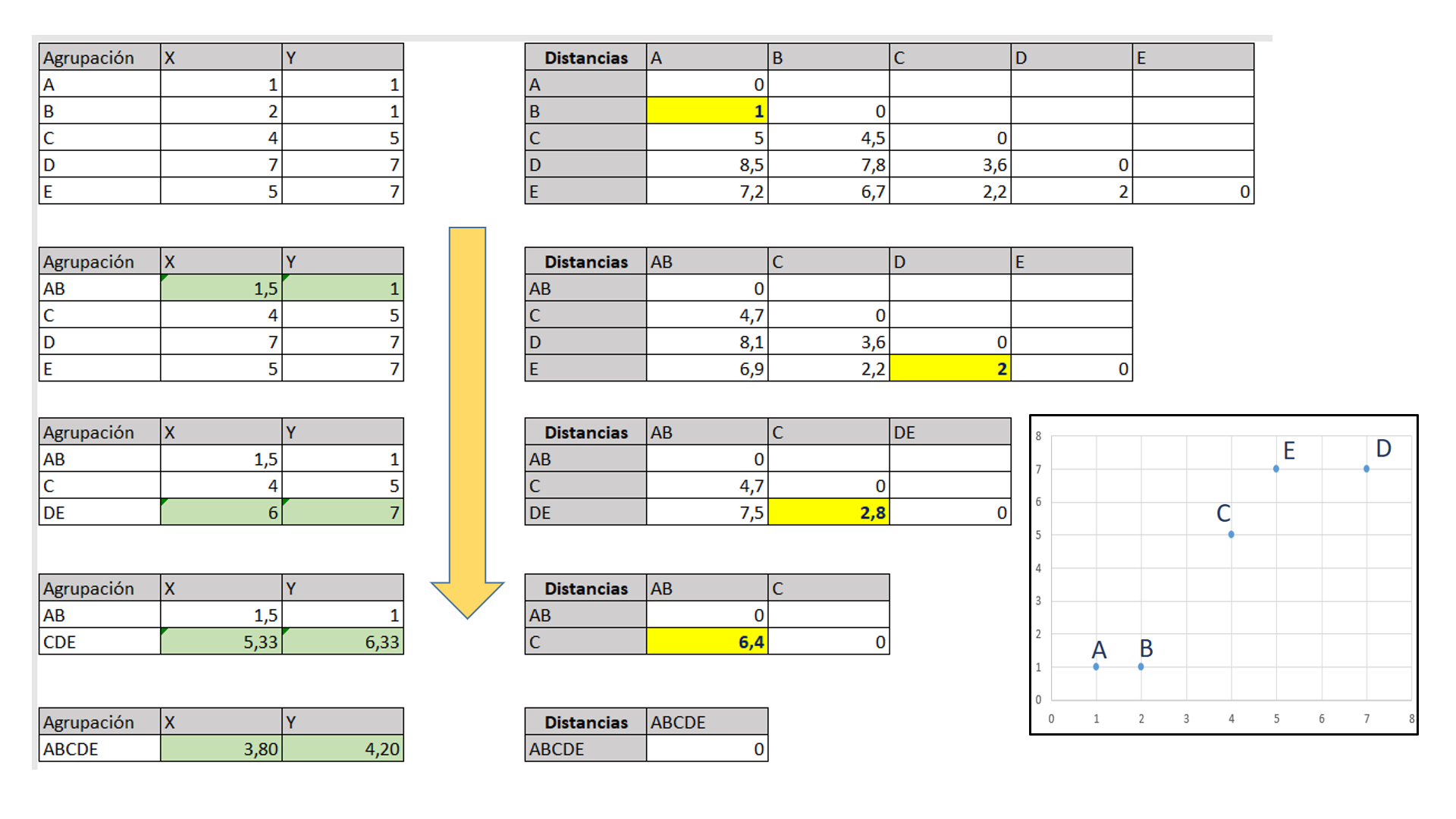
Ejemplo simple de una agrupación jerárquica¶
Un ejemplo simple del proceso de agrupación jerárquica donde se utiliza la distancia euclídea para calcular la matriz de distancias se muestra a continuación.
En cada paso se forma un nuevo grupo que implica el recálculo de las coordenadas de su centroide (en verde).
Dendograma con el resultado del ejemplo¶
Se muestran las posibles soluciones en función del nivel de agrupación

Caso de uso de la similitud¶
En el caso de usar una similitud el algoritmo sería igual pero sustituyendo la matriz de distancia por una de similitud. La diagonal principal serían unos y el cálculo de las similitudes entre dos elementos sería como se indica en el ejemplo que aparece a continuación.
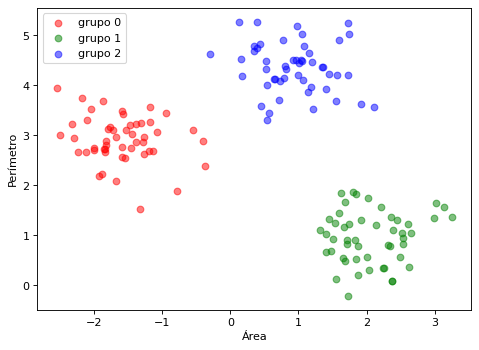
Ejemplo sencillo sobre un conjunto de puntos generados aleatoriamente¶
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
### Se dibujan los grupos
p = figure(width=500, plot_height=300)
p.circle(X[:,0], X[:,1], size=4, color="navy", alpha=0.5, legend_label="Puntos")
##p.line(X[:,0], lr.predict(Xd), line_color="green", line_width=3, line_alpha=0.6, legend_label="Cuadratica")
p.legend.location='top_left'
p.legend.click_policy="hide"
show(p)
Se resuelve un cluster aglomerativo con scikit-learn que es AgglomerativeClustering, cuyos parámetros más importantes son:
n_clusters (int o None, default=2). El número de clústeres a buscar. Debe ser None si distance_threshold no es None.
affinity (str o función llamable, default=’euclidean’). Métrica utilizada. Puede ser “euclidian”, “l1”, “l2”, “manhattan”, “cosine” o “precomputed”. Si la linkage es “ward”, solo se acepta “euclidean”. Si es “precomputed”, se necesita una matriz de distancia (en lugar de una matriz de similitud) como entrada para el método de ajuste.
compute_full_tree (‘auto’ or bool, default=’auto’). Para la ejecución hasta construir n_clusters.
linkage (‘ward’, ‘complete’, ‘average’, ‘single’, default=’ward’).
distance_threshold (float, default=None), es el umbral de distancia de vinculación por encima del cual los clústeres no se fusionarán. Si no es None, n_clusters debe ser None y compute_full_tree debe ser True.
compute_distances (bool, default=False). Calcula las distancias entre los clústeres incluso si no se utiliza la distancia umbral (distance_threshold). Sirve para hacer la visualización de dendrogramas, pero introduce una sobrecarga computacional y de memoria. (Nuevo en versión 0.24)
Según los valores de linkage:
‘ward’ minimiza la varianza de los grupos que se fusionan.
‘average’ usa el promedio de las distancias de cada observación de los dos conjuntos.
‘complete’ utiliza las distancias máximas entre todas las observaciones de los dos conjuntos.
‘single’ utiliza el mínimo de las distancias entre todas las observaciones de los dos conjuntos.
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')
y_ag = ac.fit_predict(X)
etiquetas=np.unique(y_ag)
import matplotlib.pyplot as plt
names = ['grupo 0', 'grupo 1', 'grupo 2']
marcas = ['*', 'o', 's']
color = ['red', 'green', 'blue']
plt.figure(figsize=(7, 5), dpi=80)
for i in range(len(names)):
cl = i
plt.scatter(X[y_ag==cl,0], X[y_ag==cl,1], c=color[i], alpha=0.5, marker='o', label=names[i])
plt.xlabel("Área")
plt.ylabel("Perímetro")
plt.legend(loc='upper left')
plt.show()
Es posible visualizar el dendograma con la siguiente ejecución¶
cluster_dist = AgglomerativeClustering(distance_threshold=0, n_clusters=None)
cluster_dist.fit(X)
AgglomerativeClustering(distance_threshold=0, n_clusters=None)
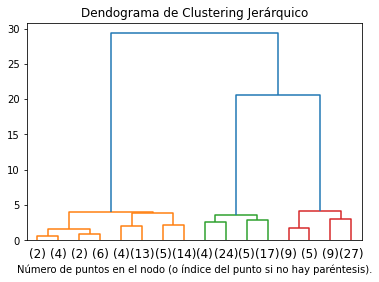
plt.title('Dendograma de Clustering Jerárquico')
# plot the top three levels of the dendrogram
plot_dendrogram(cluster_dist, truncate_mode='level', p=3)
plt.xlabel("Número de puntos en el nodo (o índice del punto si no hay paréntesis).")
plt.show()
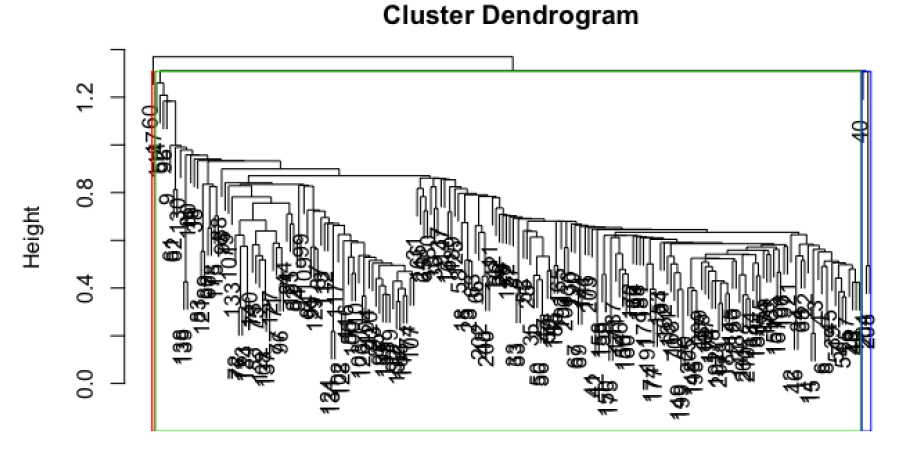
El encadenamiento simple: tiende a encadenar individuos sueltos y no grupos.
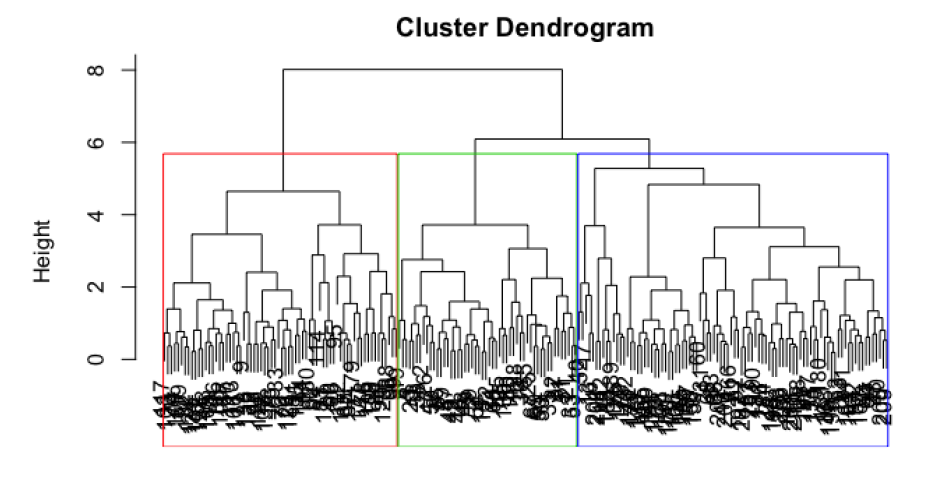
El encadenamiento completo: es menos sensible a atípicos.
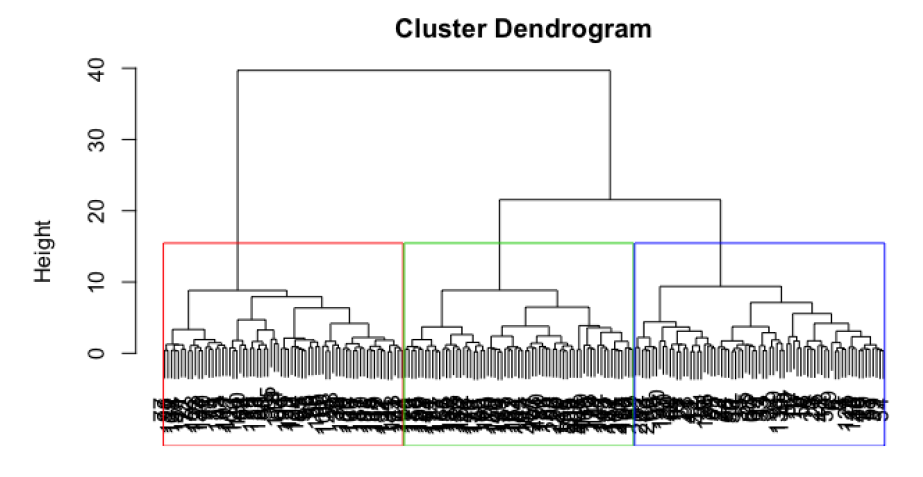
Ward tiende a formar grupos esféricos aunque los grupos no lo sean
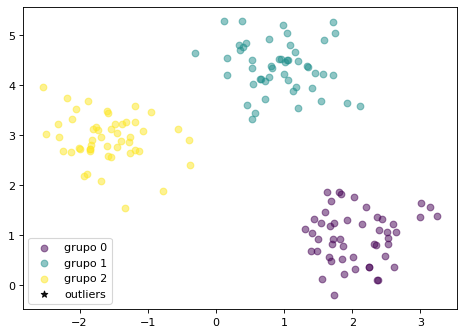
Clustering por densidad. DBSCAN¶
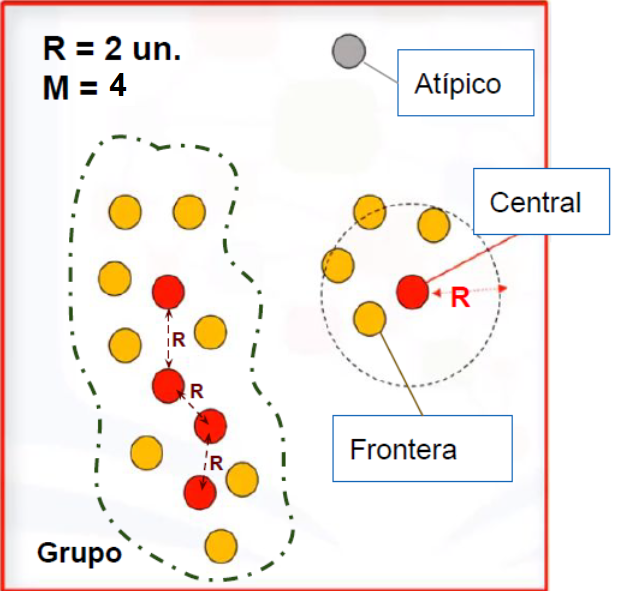
Un tercer modo de clustering es el Density-Based Spatial Clustering of Applications with Noise (DBSCAN). Agrupa áreas de alta densidad quitando los puntos atípicos o outliers. Cada grupo se forma por la unión de puntos centrales R-vecinos junto con sus puntos frontera. Los puntos outliers se descartan. La densidad se basa en R, el radio de vecindad y M, mínimo número de vecinos para definir un cluster. Un punto se denomina central si dentro de su R-vecindad hay al menos M puntos. Un punto se denomina frontera si está en la R-vecindad de un central, pero no tiene M R-vecinos. Un punto atípico o outlier es aquel que ni es central, ni frontera.
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=1, min_samples=2, metric='euclidean')
y_db = db.fit_predict(X)
np.unique(y_db)
array([0, 1, 2])
from bokeh.palettes import viridis
colors = viridis(len(np.unique(y_db)))
plt.figure(figsize=(7, 5), dpi=80)
for i in range(len(np.unique(y_db))):
cl = i
grupo = "grupo " + str(i)
plt.scatter(X[y_db==cl,0], X[y_db==cl,1], c=colors[i], alpha=0.5, marker='o', label=grupo)
cl=-1
plt.scatter(X[y_db==cl,0], X[y_db==cl,1], c="black", alpha=0.9, marker='*', label="outliers")
plt.legend(loc='lower left')
plt.show()