import numpy as np
El Algoritmo Genético¶
Pasos elementales¶
Codificación del problema en genotipos/fenotipos
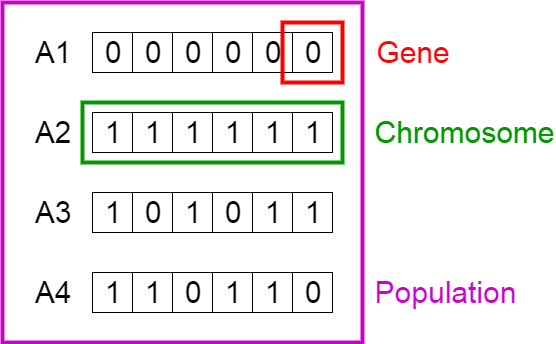
Generación inicial de una población de genotipos
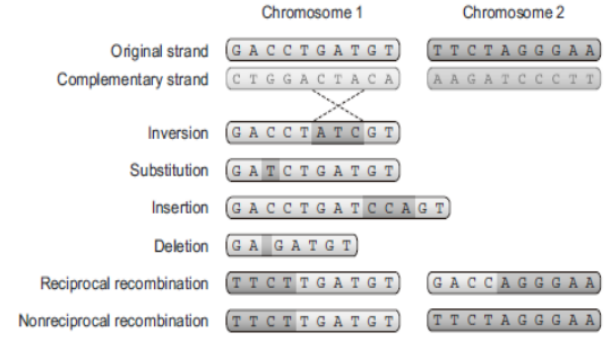
Replicación con variación (inversión o entrecruzamiento)
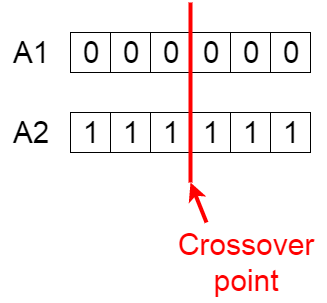
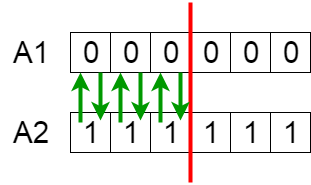
Nuevos individuos (hijos)
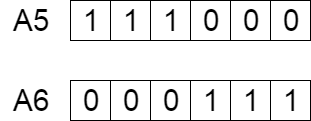
Mutación (por dígito)

Selección de los mejores fenotipos/genotipos
Función fitness
Repetición hasta convergencia.
Comprobación e interpretación del resultado en el problema original.
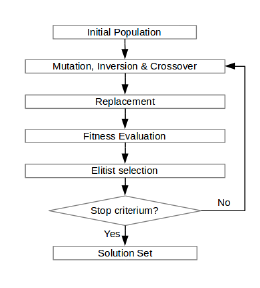
Esquema general¶
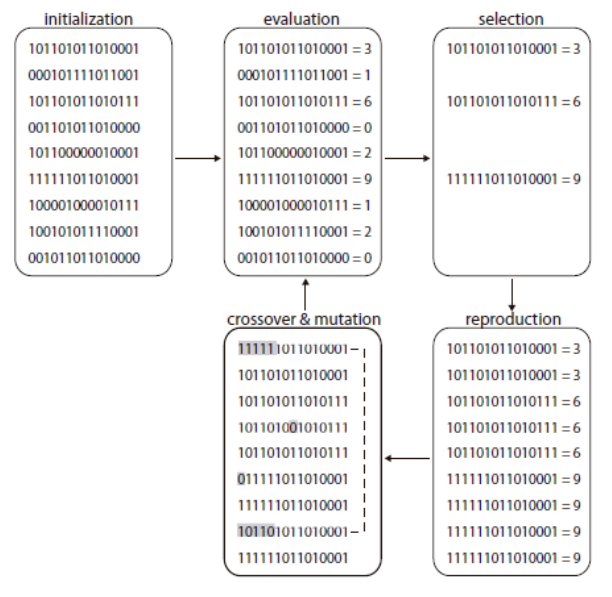
Ejemplo¶
Convergencia¶
La convergencia de los GA es un problema abierto
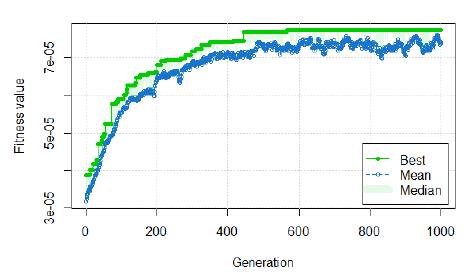
No existe una teoría general que asegure hacia dónde se dirige un GA en problemas con cierta complejidad. No obstante, existen resultados generales que aseguran la convergencia en determinadas condiciones:
Otros algoritmos de optimización¶
La evolución ha dado lugar a estrategias colectivas que aumentan la posibilidad de supervivencia del grupo.
Algoritmos de optimización genéricamente denominados enjambre (Particle Swarm Optimization, PSO)
A diferencia de los algoritmos genéticos que buscan el óptimo mediante la competición de individuos, los PSO lo hacen cooperando
Otro grupo de algoritmos de optimización bioinspirados: Ant Colony Optimization, basados en la estrategia de búsqueda de hormigas
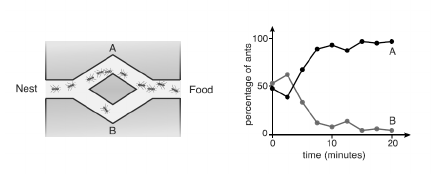
Las hormigas se disponen en una red y su movimiento por la misma depende del nivel de feromonas y las visibilidades (distancias) de los arcos que unen los nodos (posiciones).
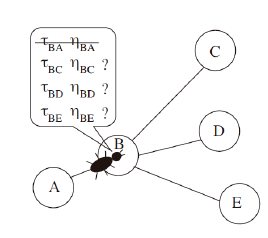
Este tipo de algoritmos ha permitido resolver problemas de gran complejidad como el problema del viajante de comercio (Travelling Salesman Problem)