Capítulo 6: Mapas Autoorganizativos¶
En este capítulo se estudian los Mapas Autoorganizativos de Teuvo Kohonen. En inglés Self Organizing Map (SOM).
Motivación¶
Existen, cada vez más y en particular en las ciencias ómicas, grandes bases de datos donde no hay una variable respuesta.
Podemos usar la idea de espacio vectorial para conceptualizar estas bases de datos. Cada instancia es un punto (vector) en \(\mathbb{R}^N\), donde \(N\) es el número de características/atributos/features de cada instancia.
En muchos casos sucede que datos cercanos en este espacio representan actividad/información similar
nubes de puntos.
La interpretación de los datos es más lenta que su generación. En muchos casos los métodos convencionales de estadística multivariante no funcionan bien. Algunas causas pueden ser:
ratio signal-to-noise bajo
missing data
small sample sizes relative to huge gene volumes
Los datos no pueden ser descritos de manera satisfactoria con los parámetros estadísiticos de bajo orden (media, varianza), las distribuciones no son Gaussianas, los estadísticos no son estacionarios. Las relaciones funcionales no son lineales en la mayor parte.
Son necesarios métodos adaptativos o redes-neuronales, que sean eficientes computacionalmente.
Inspección visual¶
Visualizar los datos es un paso crucial para descubrir relaciones entre ellos (e.g. genes y muestras)
Se buscan algorimos de
clustering
proyección
visualización que preserven la topología (forma y densidad) de los datos multidimensionales.
Objetivo: explorar la estructura geométrica de una representación bajo-dimensional que conserve la topología para descubrir relaciones/procesos/información (biológicos) significativas
Estamos casi limitados por visualizaciones tridimensionales: es necesario reducir la dimensión
El SOM¶
Los Self-Organising Maps (SOMs) son un algoritmo de aprendizaje no supervisado que permite visualizar datos en altas dimensiones mediante representaciones en dimensiones menor (típicamente dim=2). Este algoritmo ha resultado ser adecuado para el análisis de datos multidimensionales por su habilidad para preservar la topología de los mismos.
El SOM produce, usualmente, un grid hexagonal en dos dimensiones de los nodos del mapa. Cada nodo del mapa tiene asociado un vector prototipo del espacio mayor \(\mathbb{R}^N\) donde viven los datos. A esta disposición se la conoce como codebook matrix.
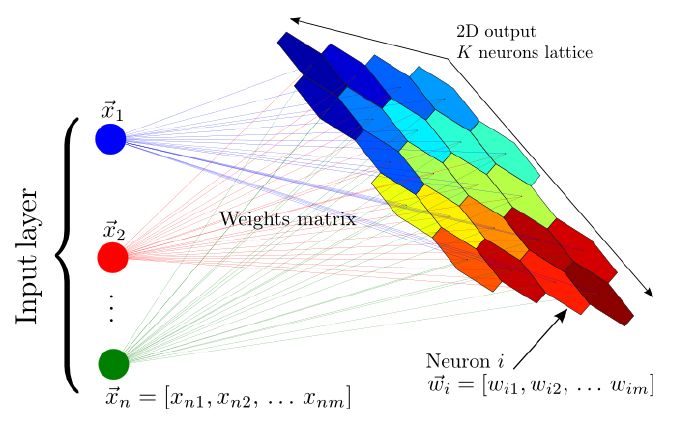
Fig. 24 Nodos y vectores prototipo¶

Fig. 25 Ejemplo de _mapa- SOM¶
El resultado del algoritmo resulta adecuado para la inspección visual del científico.
En particular, usando datos genómicos, el SOM produce un mapa que:
genes con patrones de actividad similares (vectores de actividad) son asociados con el mismo nodo o nodos cercanos en el mapa
la distribución de genes en el mapa bidimensional es semejante a la distribución en el espacio de mayor dimensión
Aplicaciones en biotecnología¶
El SOM se utiliza con mucha frecuencia en biotecnología. En la sección 6.4 Aplicaciones en biotecnología pueden verse algunas.
Bibliografía genérica¶
Práctica¶
En la primera práctica veremos cómo implementar el algoritmo SOM en una dimensión
Veremos cómo realizar el clustering de regiones vinícolas
Aplicaremos el SOM para el estudio de comunidades microbianas
Objetivos¶
Entender los fundamentos del SOM en un caso unidimensional
Aplicación los paquetes SOM para agrupar los datos
wineVisualización los clusters
Aplicación al estudio de la formación de comunidades bacterianas
