01 Introducción al Aprendizaje Automático¶

import matplotlib.pyplot as plt 
%matplotlib inline
import pandas as pd
import numpy as np
from skimage import io
from IPython import display

#

La asignatura de Aprendizaje Automático es un compendio de nuevas técnicas de análisis de datos avanzados que de la mano de la estadística y de los avances de la programación han abierto un nuevo horizonte en campos hasta ese momento vedados al análisis.

Uno de esos campos es sin lugar a duda los campos de la biología, que por la complejidad de sus modelos se encontraba fuera de muchos de los avances que la física matemática había aplicado a otros campos de la ingeniería como la electrotecnia y electrónica, la termodinámica o la mecánica de materiales por ejemplo.

Pero incluso los modelos informáticos inspirados en procesos biológicos se han constituido en herramientas de propósito general para construir los esquemas de trabajo, caso de las redes neuronales, o resolver problemas generales, caso de la aplicación de los algoritmos genéticos a la solución de problemas generales de optimización.

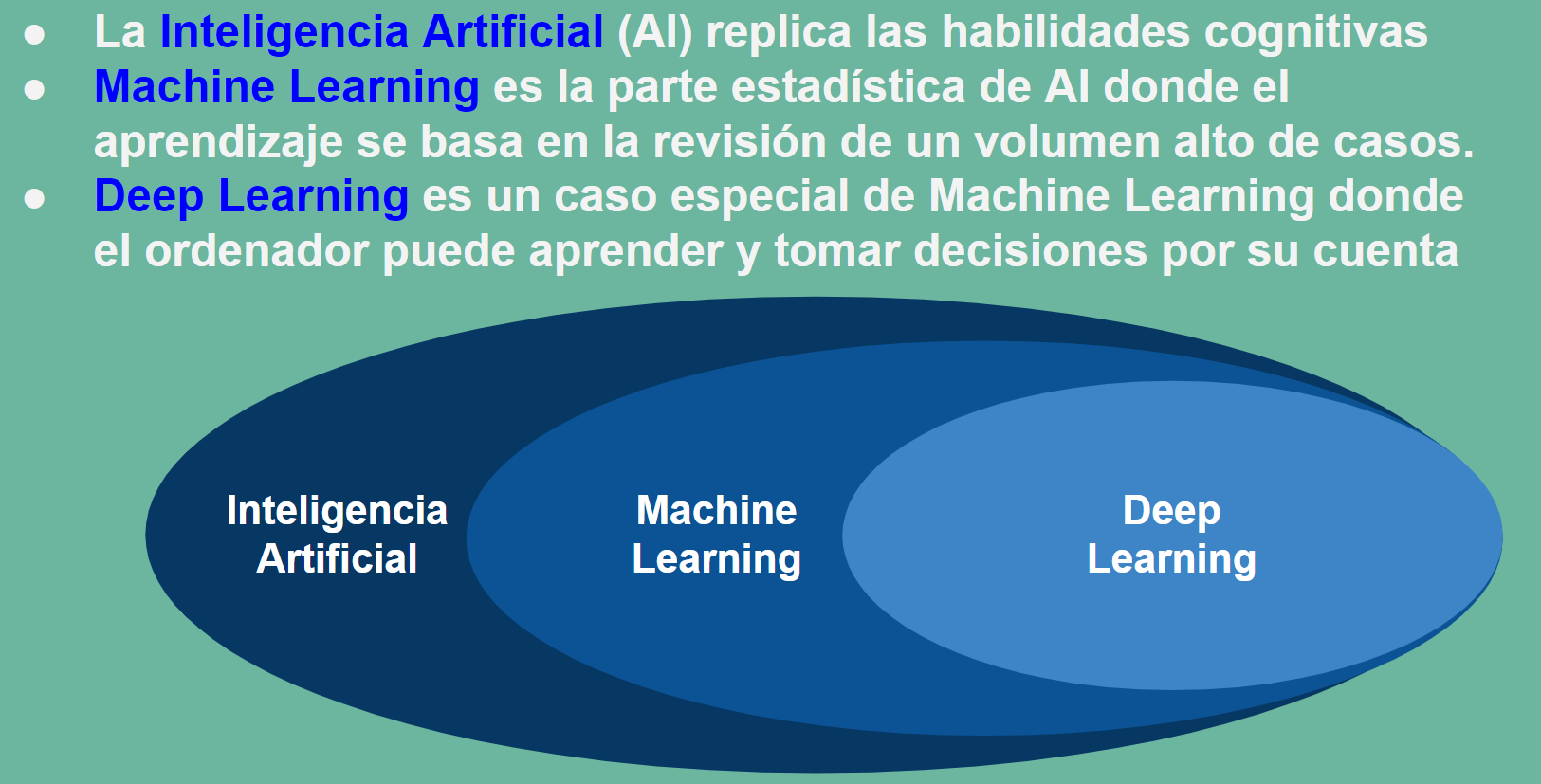
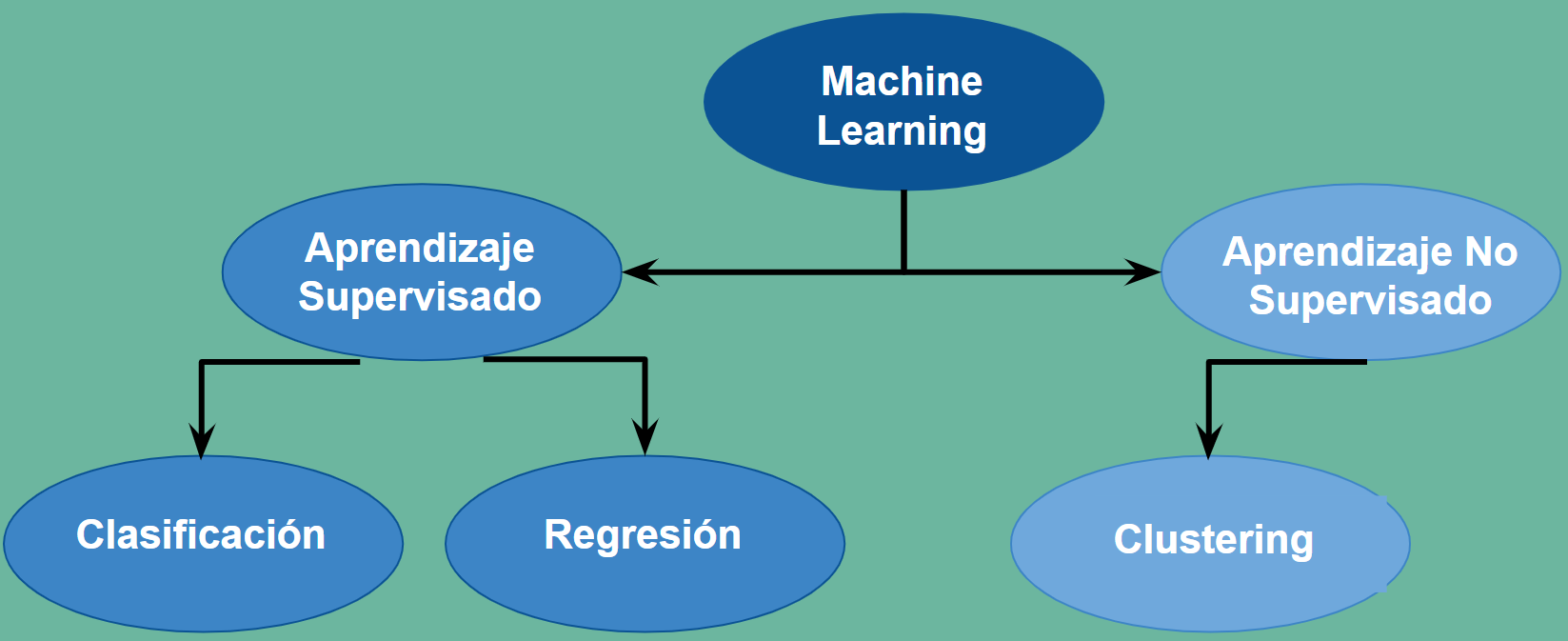
Aprendizaje supevisado vs no supevisado. Regresión vs Clasificación¶

El Aprendizaje Automático hace referencia a la preparación de un modelo entrenado estadisticamente donde se correlacionan unas observaciones, llamadas $X$ con una variable objetivo llamada $Y$. Durante el entrenamiento se construye un modelo que relaciona las observaciones recogidas en el conjunto $X$ con la variable recogida en el conjunto $Y$, que son observaciones reales conocidas de antemano.

Una vez ajustado el modelo servirá para predecir valores $Y$, objetivos desconocidos, sobre un conjunto de nuevas observaciones $X$. Esto es lo que se denomina aprendizaje supervisado, porque en el entrenamiento el disponer de objetivos conocidos $Y$ de unas observaciones $X$ permite supervisar el entrenamiento.

Finalmente hay casos en que ni siquiera conocemos ninguna variable objetivo. Simplemente nos piden que establezcamos una clasificación, (buena, regular, mala) por ejemplo, sobre un conjunto de observaciones de las que no tenemos experiencia previa. En estos casos estaremos hablando de aprendizaje no supervisado. Se aplicarán métodos que permiten hacer clasificaciones genéricas no condicionadas por una experiencia previa.

En el aprendizaje supervisado podemos encontrarnos con que los valores $Y$ sean continuos, cualquier valor de los números reales. En este caso los métodos supervisados a aplicar son las Regresiones. Mientras que si $Y$ toma sólo un conjunto discreto de valores, supongamos $ \{0, 1, 2, ..., k\} $ hablamos de métodos de Clasificación. Resumiendo una primera clasificación del Aprendizaje Automático puede ser:

Aprendizaje Supervisado. Cuando el modelo se ajusta a partir de valores conocidos $X$ e $Y$
- Regresiones. Cuando los valores que toman $Y$ son continuos
- Clasificaciones. Cuando los valores que toman $Y$ son discretos
Aprendizaje no Supervisado. Cuando partimos de valores $X$ para ajustar un modelo.

Las matrices $X$ e $Y$¶

Un conjunto de características $X$ se puede definir como una matriz de $N$ filas y $p$ columnas. Las $N$ filas hacen referencia al numero de observaciones registradas o número de individuos de la muestra de partida o entrenamiento. Mientras que $p$ es el número de características observadas y hace referencia a la dimensión de las observaciones. En cada individuo del conjunto recogemos $p$ caracteristicas distintas. Si estamos haciendo un estudio médico sobre 1.000 individuos, $N=1.000$ y si a cada individuo le medimos la presión arterial, el nivel de glucosa y el nivel de colesterol, $p=3$. Podremos recoger los datos de nuestro conjunto de entrenamiento en una matriz $1.000 \times 3$.

\[\begin{split}X=\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N1} & x_{N2} & \cdots & x_{Np} \\ \end{bmatrix}\end{split}\]

Si el estudio médico es un modelo supervisado las variables objetivo $Y$ que permiten entrenar el modelo se pueden definir como una matriz columna de $N$ filas o una matriz $N \times 1$

\[\begin{split}Y=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \\ \end{bmatrix}\end{split}\]

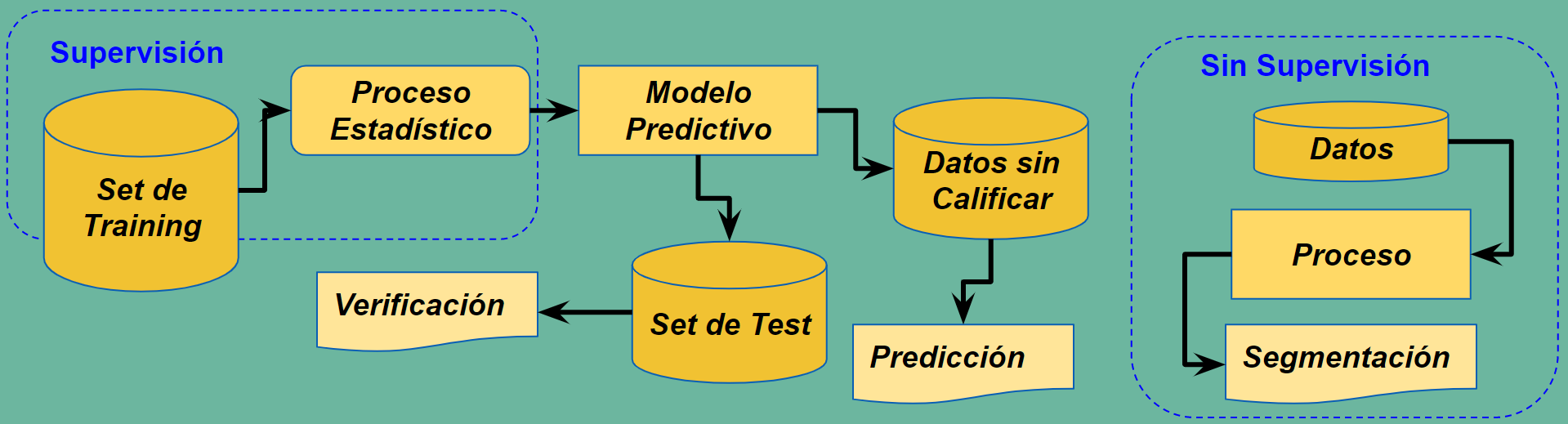
Los conjuntos de entrenamiento y validación, train y test, en el aprendizaje automático¶

El ajuste del modelo estadistico de un método supervisado se realiza sobre una parte de los conjuntos $X$ e $Y$ de partida. Se hace una partición tanto de $X$ como de $Y$ en dos subconjuntos. El primero, que se denomina de entranamiento o train se utiliza para hacer realmente el ajuste del modelo. Y este ajuste se valida en el subconjunto que se ha reservado a tal fin y al que se da el nombre de conjunto de test o validación.

Esto es así porque los métodos de ajuste pueden conseguir una convergencia sobre el conjunto de entrenamiento que sea ficticia, lo que se llama sobreajuste, y luego al validar se comprueba que el ratio de éxito es muchísimo menor. Esto puede ser así porque realmente el modelo no tenga convergencia o correlación real.

Regresión Simple¶

Las regresiones no serán parte del curso. No obstante y a efectos de poner contexto y observar que algunos algoritmos de la regresión se utilizan en clasificación, se hecha un vistazo a la regresión simple o lineal

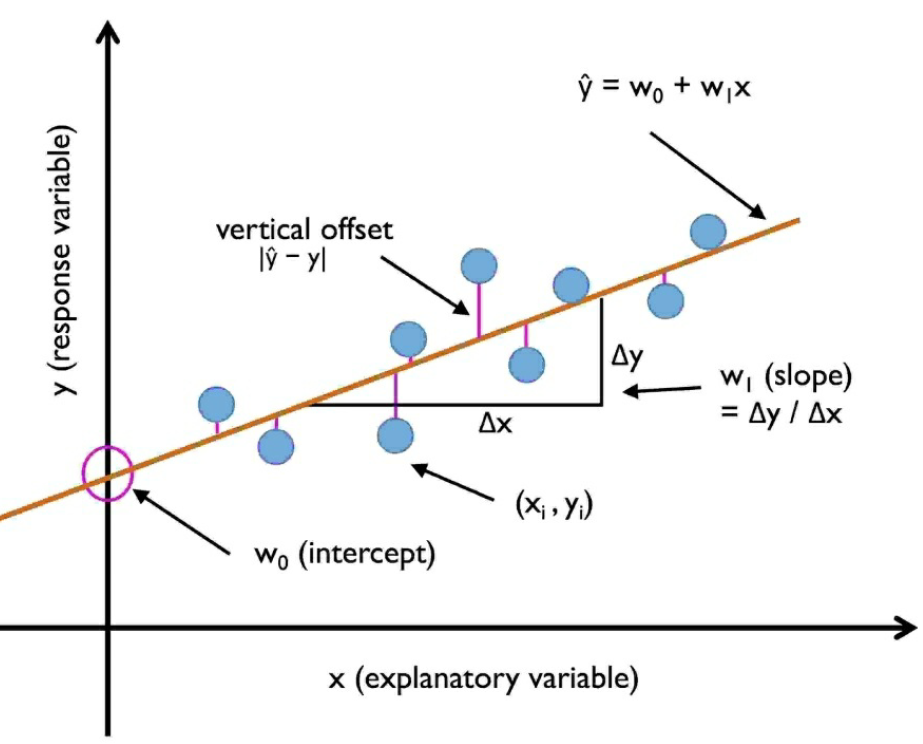
El objetivo de una regresión simple es ajustar la relación entre una característica (una variable independiente o explicita $x$) y una respuesta con valores continuos (variable objetivo $y$). La ecuación del modelo lineal es:

\[y=w_0 + w_1x\]

El peso $w_0$ es la intersección con el eje y. El peso $w_1$ es el coeficiente de la variable independiente.

En el siguiente gráfico se representan las características de una regresión lineal. La recta regresión minimiza los errores residuales entre un valor real $y$ y su valor estimado por la recta $\hat{y}$. Estos errores o residuos se denominan en inglés offsets o residuals.

Regresión Múltiple¶

Si en lugar de una variable explicita, tenemos varias variables explicitas como características de las que depende la variable objetivo la regresión lineal adopta la forma

\[y=w_0x_0+w_1x_1+...+w_mx_m=\displaystyle\sum_{i=0}^m w_ix_i\]

Donde $w_0$ es la intersección con el eje y con $x_0=1$

Si el número de características es 2, la regresión es un plano y tendría la siguiente representación. En general para m características la regresión es un hiperplano en el espacio $R^{m+1}$:

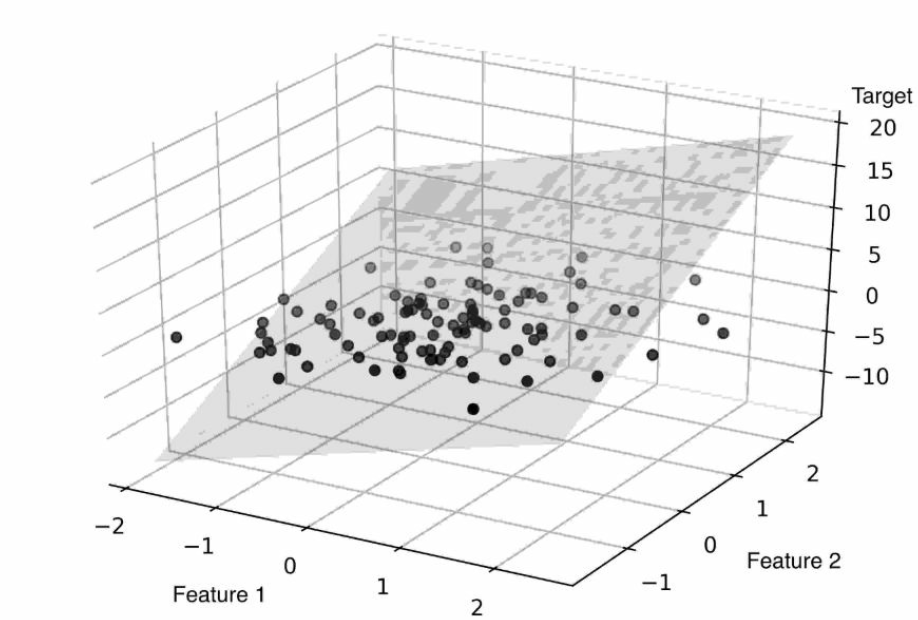
Para los ejemplos se utilizará un dataset: housing.csv. Las columnas del dataset son:

CRIM: Tasa de criminalidad per cápita por ciudad
ZN: proporción de terrenos residenciales divididos en zonas para lotes de más de 25,000 pies cuadrados.
INDUS: proporción de acres de negocios no minoristas por ciudad
CHAS: variable ficticia Charles River (= 1 si el tramo limita con el río; 0 en caso contrario)
NOX: concentración de óxido nítrico (partes por 10 millones)
RM: número medio de habitaciones por vivienda
AGE: Proporción de unidades ocupadas por sus propietarios construidas antes de 1940
DIS: distancias ponderadas a cinco centros de empleo de Boston
RAD: índice de accesibilidad a autopistas radiales
TAX: Tasa de impuesto a la propiedad de valor total por 10.000 USD
PTRATIO: relación alumno-profesor por localidad
B: $1000 (B_k - 0.63) ^ 2$, donde $B_k$ es la proporción de [personas con ascendencia Áfro-americana] por ciudad
LSTAT: porcentaje de población de menor status
MEDV: valor medio de viviendas ocupadas por sus propietarios en 1000 USD

df = pd.read_csv('data/Housing.csv', header=None, sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()

	CRIM	ZN	INDUS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0.538	6.575	65.2	4.0900	1	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0.469	6.421	78.9	4.9671	2	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0.469	7.185	61.1	4.9671	2	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0.458	6.998	45.8	6.0622	3	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0.458	7.147	54.2	6.0622	3	222.0	18.7	396.90	5.33	36.2

Ajuste por mínimos cuadrados¶

Si el número de filas del conjunto de datos no es muy elevado el ajuste de una regresión lineal se puede realizar directamente por la siguiente operación matricial (que implementa el ajuste por mínimos cuadrados):

\[w=(X^TX)^{-1}X^Ty\]

Siendo $X$ la matriz de valores de las características puestas en columna e incluyendo un 1 en la primera columna.

Dado un valor concreto de una características $x$, donde el primer elemento de la columan es un 1, su predicción es:

\[\hat{y}=w^Tx\]

La anterior fórmula matricial se deduce de minimizar los errores al cuadrado de todo el conjunto $X$, tomando el vector columna $E=Y-Xw^T$ la suma de errores al cuadrado vendrá dada por

\[C=E^TE=(Y-Xw^T)^T(Y-Xw^T)\]

Derivando $C$ con respecto a $w$ e igualando a cero:

\[X^T(y-Xw^T)=0\]

Saldría la expresión matricial anterior. Por conveniencia se ha incorporado una columna de observaciones a “1” en X para operar el coeficiente $w_0$.

Si $p=1$ la regresión se reduce a obtener $w_1=\sum_{i} \frac{(x_i-\bar{x})(y_i-\bar{y})}{(x_i-\bar{x})^2}$ e $w_0=\bar{y}-w_1\bar{x}$

$w_0$ se denomina Sesgo (Bias en inglés). El sesgo es un concepto estadístico que se refiere al error cometido al realizar el muestreo o conjunto de entrenamiento y viene definido matemáticamente como la diferencia entre la esperanza matemática menos el valor numérico.

Para más detalle consultar: An Introduction to Statistical Learning with Applications in R (Casella G. et al., 2013).

La implementación directa de la operación matricial es en el ejemplo anterior:

# Se añade una primera columna de unos
X = df.iloc[:, :-1].values
y = df['MEDV'].values
Xb = np.hstack((np.ones((X.shape[0], 1)), X))
w = np.zeros(X.shape[1])
z = np.linalg.inv(np.dot(Xb.T, Xb))
w = np.dot(z, np.dot(Xb.T, y))
print("Coeficientes", w)

Coeficientes [ 3.64594884e+01 -1.08011358e-01  4.64204584e-02  2.05586264e-02
  2.68673382e+00 -1.77666112e+01  3.80986521e+00  6.92224640e-04
 -1.47556685e+00  3.06049479e-01 -1.23345939e-02 -9.52747232e-01
  9.31168327e-03 -5.24758378e-01]

Regresión Lineal con sk-learn¶

Lo normal es emplear los métodos de la clase LinearRegression sk-learn

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)

import matplotlib.pyplot as plt
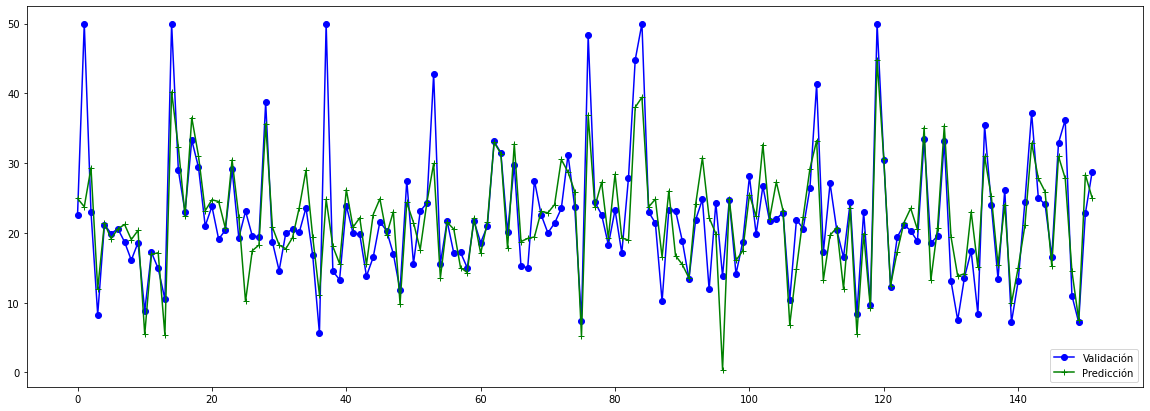
plt.figure(figsize=(20,7))
plt.plot(y_test, color='blue', marker='o', label='Validación')
plt.plot(y_test_pred, color='green', marker='+', label='Predicción')
plt.legend(loc='lower right')

<matplotlib.legend.Legend at 0x7f95f8fe8c70>

Alternativa al ajuste directo por mínimos cuadrados (valor de $N$ elevado)¶

Se va a implementar el algoritmo ADAptive LInear NEuron (Adaline), definiendo una función de coste $C()$ a minimizar ajustando los pesos via Gradiente Descenso o Gradiente Descenso Estocástico.

La función de coste en Adaline es Suma de Errores al Cuadrado (SSE):

\[C(w)=\frac{1}{2}\displaystyle\sum_{i=1}^n (y^{(i)}-\hat{y}^{(i)})^2\]

Siendo $\hat{y}$ el valor predicho por el ajuste lineal con los pesos: $$\hat{y}=w^Tx$$

El valor $\frac{1}{2}$ aparece por conveniencia, dado que si optimizamos una función también su mitad. Y al derivar el cuadrado, se va el $2$ con el $\frac{1}{2}$. Derivada necesaria, pues el gradiente se obtiene de la derivada parcial

class LinearRegressionGD(object):
    def __init__(self, eta=0.001, n_iter=20):
        self.eta = eta
        self.n_iter = n_iter
    def fit(self, X, y):
        self.w_ = np.zeros(1 + X.shape[1])
        self.cost_ = []
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = (y - output)
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0
            self.cost_.append(cost)
        return self
    
    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]
    
    def predict(self, X):
        return self.net_input(X)

La mayor correlación de la variable objetivo MEDV es LSTAT, pero en el dibujo anterior no se veía que la relación fuese bastante lineal. Por lo que se elige RM que tiene una correlación bastante parecida y una relación mucho más lineal.

X = df[['RM']].values
y = df['MEDV'].values
from sklearn.preprocessing import StandardScaler
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
## np.newaxis es para introducir una nueva dimensión al array
## flatten es para quitar es dimensión de más
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()
lr = LinearRegressionGD()
lr.fit(X_std, y_std)

<__main__.LinearRegressionGD at 0x7f95f8886640>

Para ver como se ha ido ajustando el error SSE con los sucesivos pasos o épocas del algoritmo:

from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.models import ColumnDataSource
from bokeh.models.glyphs import Line
output_notebook()

p = figure(width=400, plot_height=200)
source = ColumnDataSource(dict(x=range(1, lr.n_iter+1), y=lr.cost_))
glyph = Line(x="x", y="y", line_color="red", line_width=3, line_alpha=0.6)
p.add_glyph(source, glyph)
p.xaxis.axis_label = 'Épocas'
p.yaxis.axis_label = 'SSE'
show(p)

Loading BokehJS ...

El ajuste de la regresión contra el gráfico de dispersión sería:

from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.models import ColumnDataSource
from bokeh.models.glyphs import Line
output_notebook()

p = figure(width=400, plot_height=400)
w_x=X_std
w_y=lr.w_[0] + lr.w_[1]*w_x
source = ColumnDataSource(dict(x=w_x, y=w_y))
glyph = Line(x="x", y="y", line_color="red", line_width=3, line_alpha=0.6)
p.add_glyph(source, glyph)
p.circle(X_std[:,0], y_std, size=2, color="navy", alpha=0.5)
p.xaxis.axis_label = 'Numero de Habitaciones estandarizado (RM)'
p.yaxis.axis_label = 'Precio en $1000 estandarizado (MEDV)'
show(p)

Loading BokehJS ...

Para volver a escalar el resultado del precio predicho en el eje Precio en $ 1000s, simplemente podemos aplicar el método inverse_transform de StandardScaler:

from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.models import ColumnDataSource
from bokeh.models.glyphs import Line
output_notebook()

p = figure(width=400, plot_height=400)
w_x= X_std
w_y=lr.w_[0] + lr.w_[1]*w_x
source = ColumnDataSource(dict(x=sc_x.inverse_transform(w_x), y=sc_y.inverse_transform(w_y)))
glyph = Line(x="x", y="y", line_color="red", line_width=3, line_alpha=0.6)
p.add_glyph(source, glyph)
y_nostd = sc_y.inverse_transform(y_std[:, np.newaxis]).flatten()
p.circle(sc_x.inverse_transform(X_std)[:,0], y_nostd, size=2, color="navy", alpha=0.5)
p.xaxis.axis_label = 'Numero de Habitaciones (RM)'
p.yaxis.axis_label = 'Precio en $1000 (MEDV)'
show(p)

Loading BokehJS ...

Introducción al Aprendizaje Automático

01 Introducción al Aprendizaje Automático¶

Aprendizaje supevisado vs no supevisado. Regresión vs Clasificación¶

Las matrices \(X\) e \(Y\)¶

Los conjuntos de entrenamiento y validación, train y test, en el aprendizaje automático¶

Regresión Simple¶

Regresión Múltiple¶

Ajuste por mínimos cuadrados¶

Regresión Lineal con sk-learn¶

Alternativa al ajuste directo por mínimos cuadrados (valor de \(N\) elevado)¶