Contents

4.5 Análisis de HMM

Tenemos tres fases:

  1. Aprendizaje: dada una lista de secuencias de sı́mbolos, ¿podemos aprender los parámetros \((\pi^{(0)} , P, E )\) de un HMM? Algoritmo de Baum-Welch.

  2. Evaluación: una vez que el modelo está ajustado, ¿cuál es la verosimilitud de una secuencia dada? Algoritmo “forward”.

  3. Descodificación: una vez que el modelo está ajustado, ¿cuál es el la secuencia de estados más probable para generar de una secuencia de sı́mbolos dada? Algoritmo de Viterbi.

4.5.1 Aprendizaje

Dos casos:

  1. Si conocemos las secuencias de estados asociadas a cada secuencia de sı́mbolos

  2. Si no los conocemos

Caso 1: conocemos las secuencias de estados asociadas a los símbolos

En proteı́nas, esto equivale a conocer la estructura secundaria de cada secuencia de aminoácidos.

  • La verosimilitud de que una secuencia de estados \(\mathcal{est}=\{x_1,\ldots,x_n\}\) genere una secuencia de símbolos \(\mathcal{sim}=\{s_1,\ldots,s_n\}\) es:

\[ \mathbb{P}\{\mathcal{est},\mathcal{sim}\}= \mathbb{P}\{X_1=x_1\}\mathbb{P}\{S_1=s_1|X_1=x_1\}\times \prod_{t=2}^{n}\mathbb{P}\{X_t=x_t|X_{t-1}=x_{t-1}\}\mathbb{P}\{S_t=s_t|X_t=x_t\} \]

  • Entonces el método de máxima verosimilitud permite estimar los parámetros como frecuencias relativas en el conjunto de entrenamiento.

Note

En el conjunto de entrenamiento

  • Probabilidades de transición:

\[ p_{ij}=\frac{\text{número de transiciones desde $X=x_i$ hasta $X=x_j$}}{\text{número de transiciones que parten de $X=x_i$}} \]

  • Probabilidades de emisión:

\[ e_{ij}= \frac{\text{número de veces que el estado $X=x_i$ emite el símbolo $S=s_j$}}{\text{número de veces que el estado es $X=x_i$}} \]

  • Vector inicial:

\[ \pi^{(0)}_{i}= \frac{\text{número de veces que el estado inicial es $X=x_i$}} {\text{número total de instancias}} \]

Caso 2: no conocemos las secuencias de estados asociadas a los símbolos

En proteı́nas, esto equivale a conocer solamente las secuencias de aminoácidos.

  • Este es el caso más frecuente en la práctica.

  • En este caso se puede aplicar el algoritmo de Baum-Welch, que estima también las probabilidades de transición aunque no conozcamos las secuencias de estados.

4.5.2 Evaluación

Warning

¡Tras la fase de aprendizaje!

Dada una secuencia de sı́mbolos (aminoácidos), ¿puedo calcular la probabilidad de observarla de acuerdo con el HMM?

  • Equivale a calcular la probabilidad marginal

\[ \mathbb{P}\{\mathcal{sim}\}= \sum_{\{x_1,\ldots,x_n\}} \mathbb{P}\{X_1=x_1\}\mathbb{P}\{S_1=s_1|X_1=x_1\}\prod_{t=2}^{n}\mathbb{P}\{X_t=x_t|X_{t-1}=x_{t-1}\}\mathbb{P}\{S_t=s_t|X_t=x_t\} \]

donde tenemos que sumar sobre todos los posibles caminos que generan la secuencia.

  • El número de posibilidades crece exponencialmente con \(n\).

  • Se usa programación dinámica para calcular la suma anterior de manera eficiente. El resultado es el algoritmo “forward”.

4.5.3 Descodificación

Warning

¡Tras la fase de aprendizaje!

Dada una secuencia de sı́mbolos (aminoácidos), ¿puedo calcular la secuencia de estados ocultos (estructuras secundarias) que maximiza la verosimilitud \(\mathbb{P}\{\mathcal{est}, \mathcal{sim} \}\)?

  • Es un proceso de máxima verosimilitud.

  • Se usa programación dinámica eligiendo la rama de mayor probabilidad en cada paso de la secuencia.

  • El resultado es el algoritmo de Viterbi.

Algoritmo de Viterbi

Para el ejemplo anterior:

\[\begin{split} \mathbf{v}_0=\left(\stackrel{H}{0.6},\quad \stackrel{C}{0.4} \right),\quad P= \stackrel{H\quad C}{% \begin{bmatrix} 0.6 & 0.4 \\ 0.3 & 0.7 \end{bmatrix}% },\quad E= \begin{matrix} H \\C \end{matrix} \stackrel{G\quad W\quad M}{% \begin{bmatrix} 0.6 & 0.3 & 0.1 \\ 0.2 & 0.4 & 0.4 \end{bmatrix}% } \end{split}\]

Tenemos una cadena con tres símbolos observados: \(G-W-M\) (en ese orden). Queremos conocer la cadena de estados subyacente más probable.

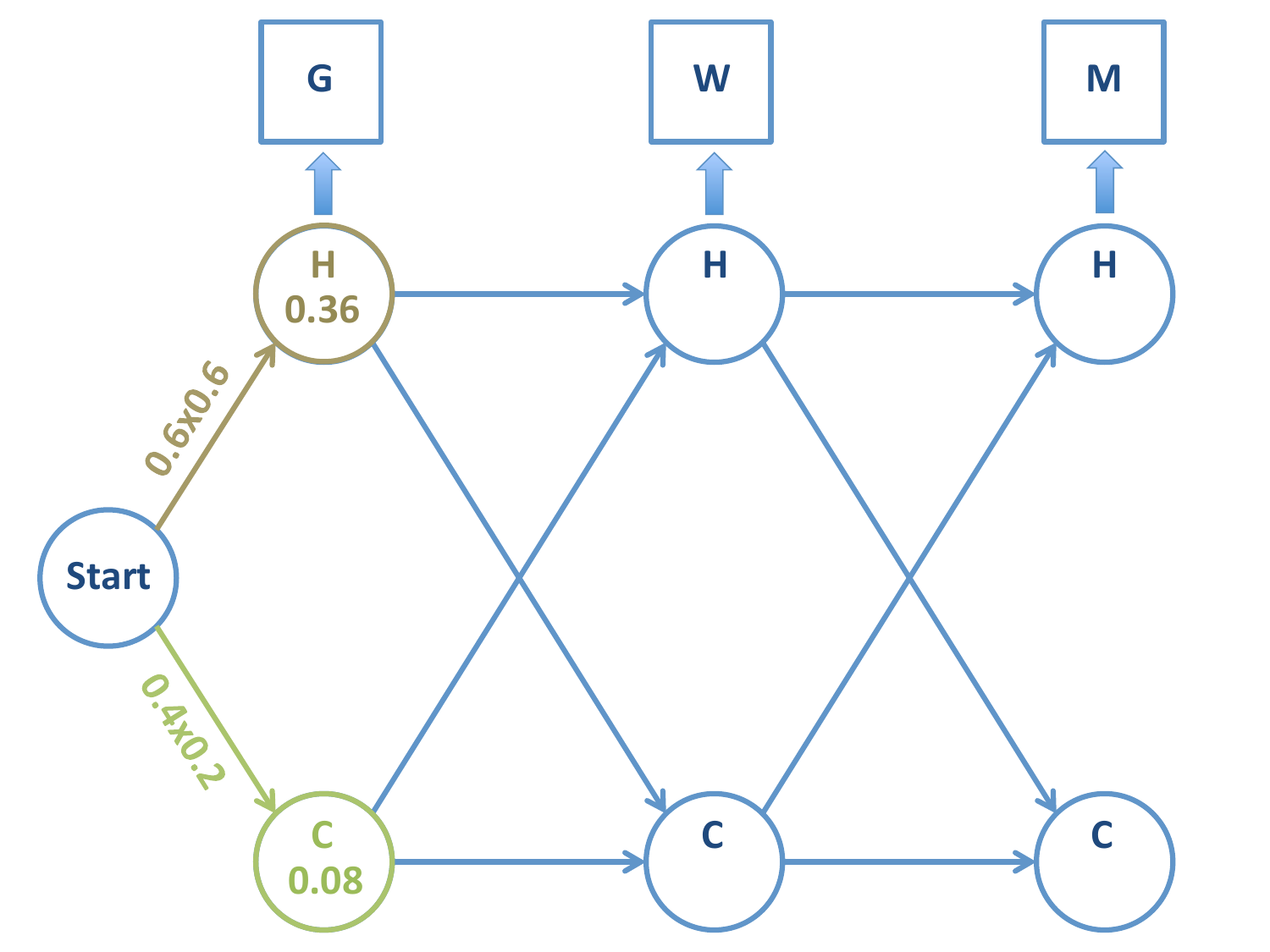
_images/hmm1.png

Fig. 13 Viterbi

\[\begin{split} \pi^{(0)}=\left(\stackrel{\color{red}{H}}{\color{red}{0.6}},\quad \stackrel{\color{blue}{C}}{\color{blue}{0.4}} \right),\quad P= \stackrel{H\quad C}{% \begin{bmatrix} 0.6 & 0.4 \\ 0.3 & 0.7 \end{bmatrix}% },\quad E= \begin{matrix} H \\C \end{matrix} \stackrel{\color{orange}{G}\quad W\quad M}{% \begin{bmatrix} \color{red}{0.6} & 0.3 & 0.1 \\ \color{blue}{0.2} & 0.4 & 0.4 \end{bmatrix}% } \end{split}\]
\[ \mathcal{L}_1(H)=\pi^{(0)}(H)\cdot E(H\rightarrow G)= 0.6 \times 0.6 = 0.36 \]
\[ \mathcal{L}_1(C)=\pi^{(0)}(C)\cdot E(C\rightarrow G)= 0.4 \times 0.2 = 0.08 \]
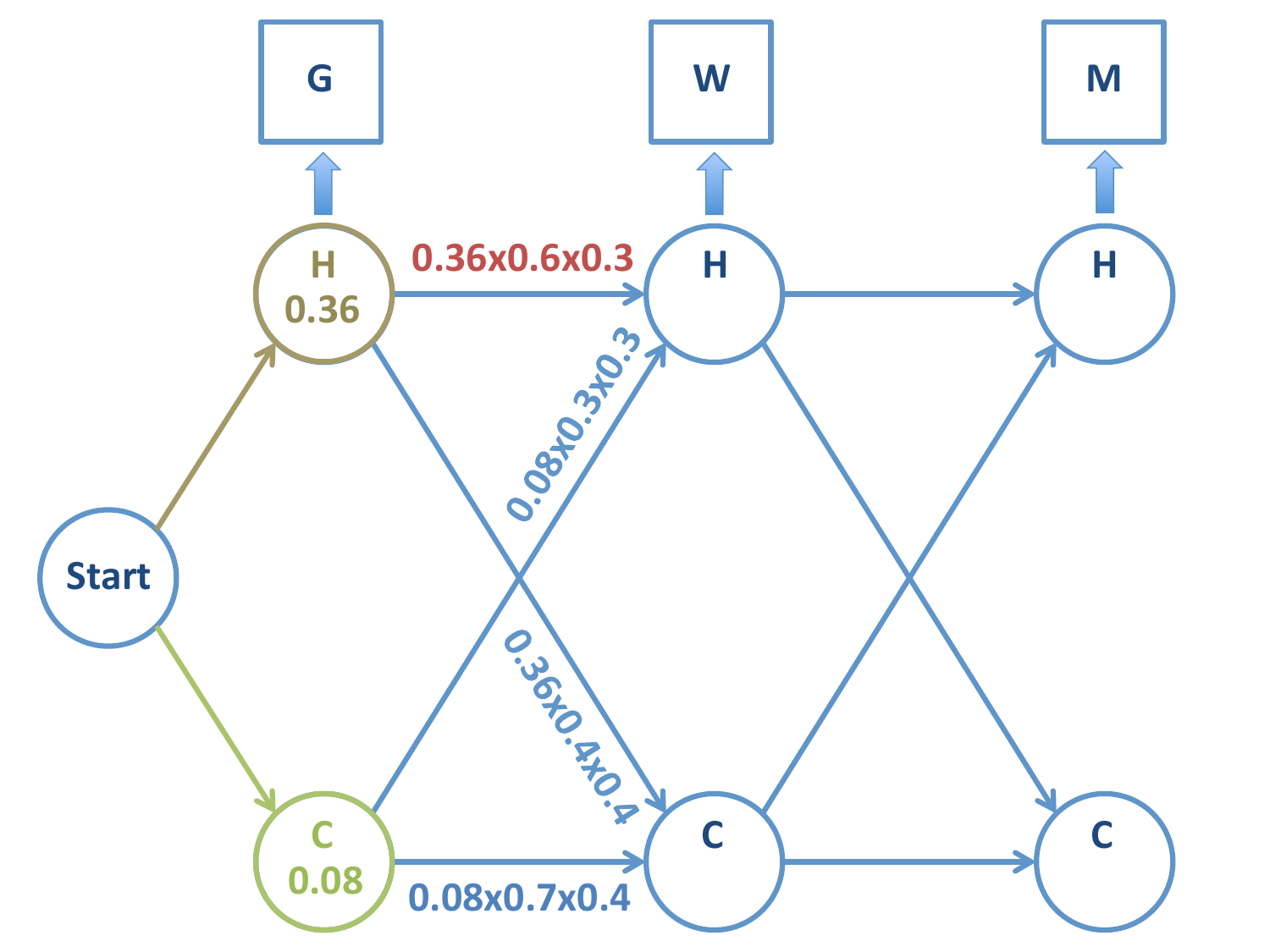
_images/hmm2.png

Fig. 14 Viterbi

Siguiente paso: calculamos las probabilidades de las 4 cadenas posibles.

Importante

Partimos de

\[\begin{split} \mathcal{L}_1=\left( \stackrel{\color{red}{H}}{\color{red}{0.36}} ,\quad \stackrel{\color{blue}{C}}{\color{blue}{0.08}} \right) ,\quad P= \stackrel{H\quad C}{% \begin{bmatrix} 0.6 & 0.4 \\ 0.3 & 0.7 \end{bmatrix}% },\quad E= \begin{matrix} H \\C \end{matrix} \stackrel{G\quad \color{orange}{W}\quad M}{% \begin{bmatrix} 0.6 & 0.3 & 0.1 \\ 0.2 & 0.4 & 0.4 \end{bmatrix}% } \end{split}\]

  • Probabilidad de la cadena \(H-H\):

\[ \mathcal{L}_1(H)\cdot P(H\rightarrow H)\cdot E(H\rightarrow W) = 0.36 \times 0.6 \times 0.3 = 0.0648 \]

  • Probabilidad de la cadena \(C-H\):

\[ \mathcal{L}_1(C)\cdot P(C\rightarrow H)\cdot E(H\rightarrow W) = 0.08 \times 0.3 \times 0.3 = 0.0072 \]

Importante

En este momento podemos rechazar la cadena \(C-H\) frente a \(H-H\), ya que la primera tiene menos probabilidad de ocurrir. Aquí radica la potencia del algoritmo de Viterbi: dejamos de calcular las probabilidades de todas las cadenas sucesivas a \(C-H\).

Note

Esta selección se hace a nivel de nodo: rechazamos uno de los caminos que llegan a un nodo.

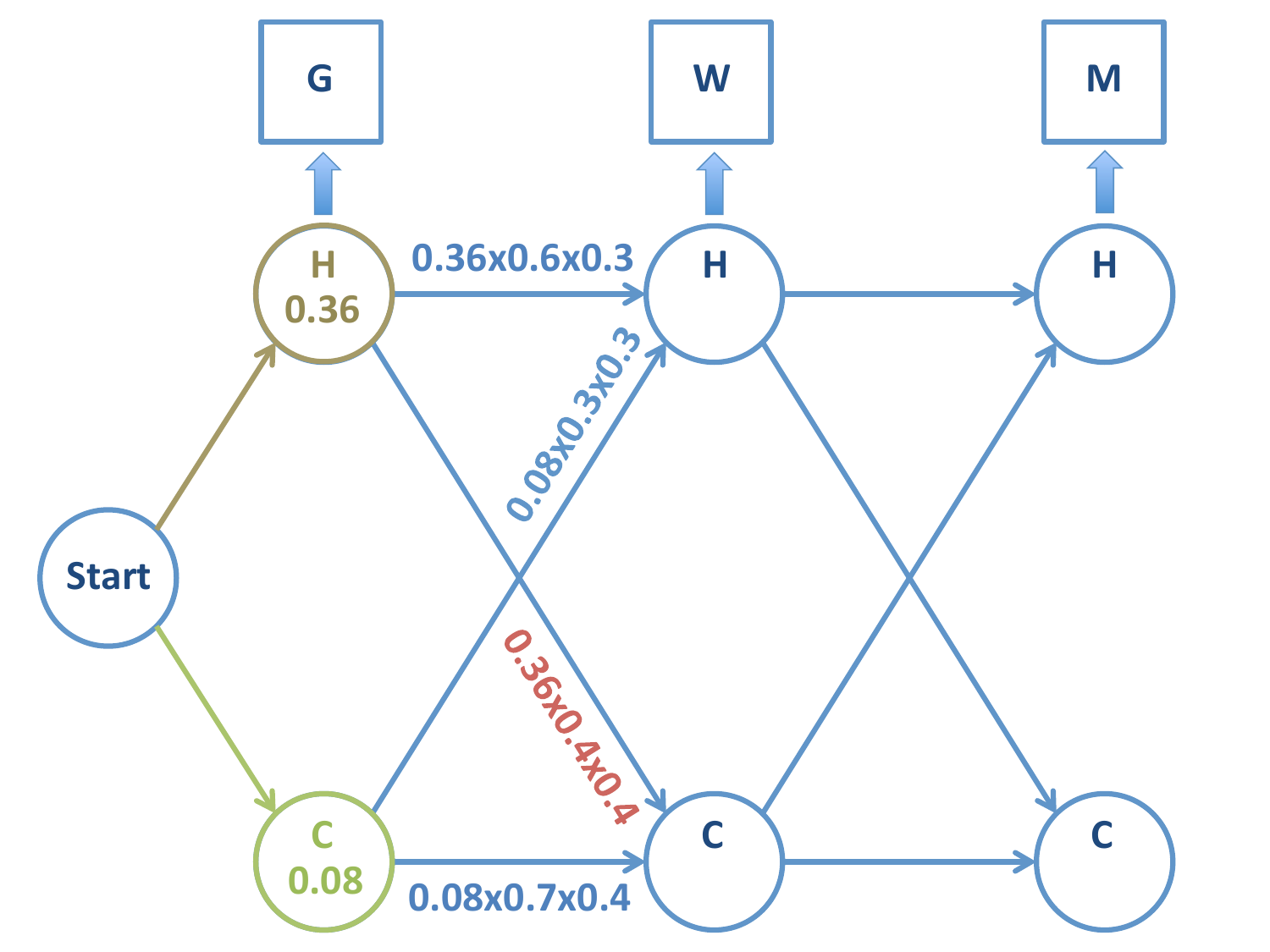
_images/hmm3.png

Fig. 15 Viterbi

  • Probabilidad de la cadena \(H-C\):

\[ \mathcal{L}_1(H)\cdot P(H\rightarrow C)\cdot E(C\rightarrow W) = 0.36 \times 0.4 \times 0.4 = 0.0576 \]

  • Probabilidad de la cadena \(C-C\):

\[ \mathcal{L}_1(C)\cdot P(C\rightarrow C)\cdot E(C\rightarrow W) = 0.08 \times 0.7 \times 0.4 = 0.0224 \]

Igualmente, aquí podemos descartar la cadena \(C-C\) frente a \(H-C\) (y todas las sucesivas cadenas de \(C-C\)).

Hemos rechazado los caminos \(C-C\) y \(C-H\), por tanto podemos rechazar que la cadena pasa por nodo \(C\) en la primera etapa.

En cada caso: tomamos el camino de mayor probabilidad y marcamos el nodo.

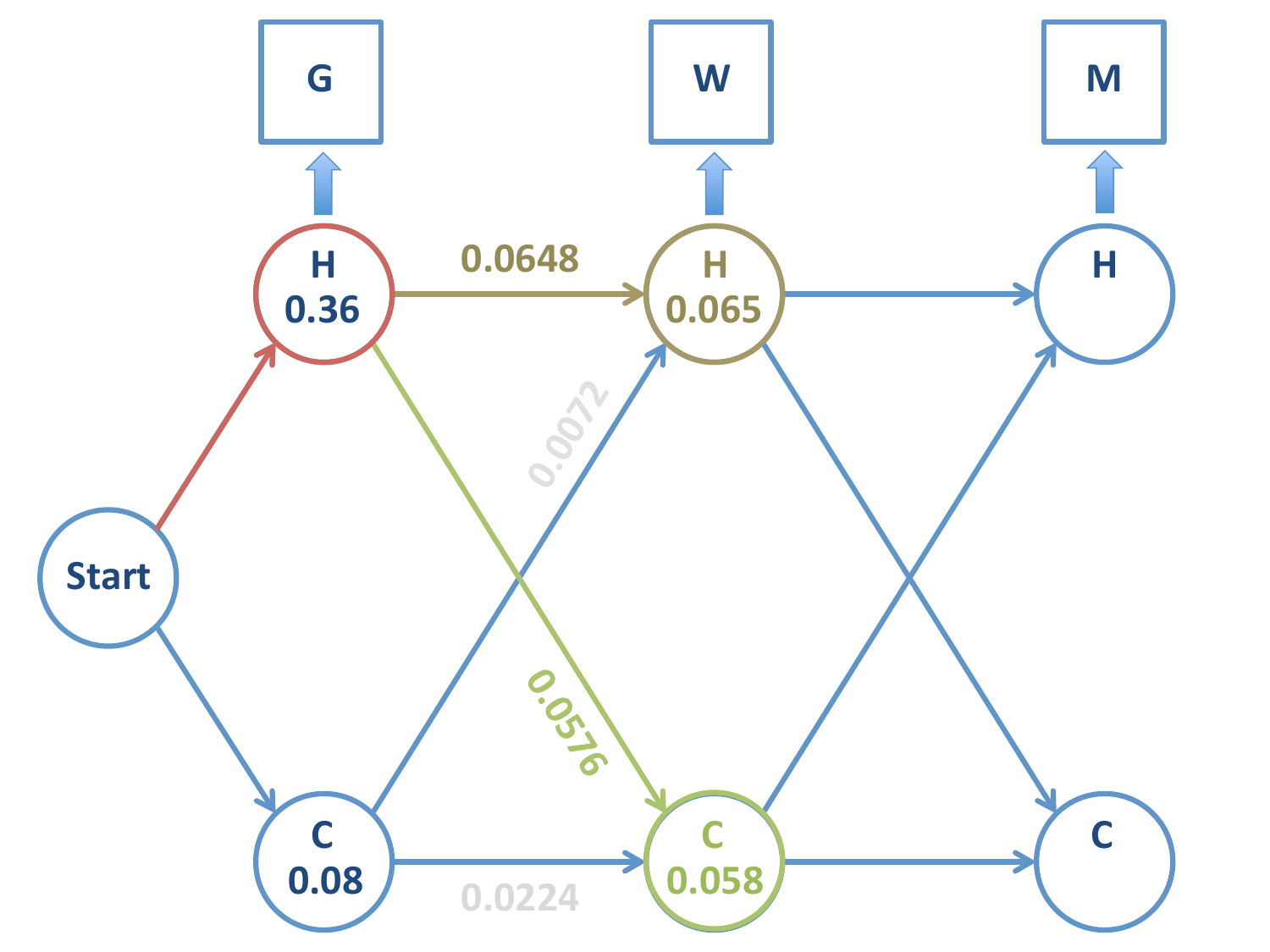
_images/hmm4.png

Fig. 16 Viterbi

Importante

NO podemos rechazar, no obstante, el nodo \(C\) en la segunda etapa de la cadena (emisión \(=W\)). En este momento disponemos de la probabilidad que la cadena sea \(H-C\) ó \(H-H\), pero la cadena de Markov continua.

Continuamos el proceso hasta la última etapa de la cadena: calculamos las probabilidades de las cadenas restantes, que son:

  • \(H-H-H\)

  • \(H-H-C\)

  • \(H-C-H\)

  • \(H-C-C\)

Note

En la tercera etapa el estado observado es \(M\)

Partimos de esta situación

\[\begin{split} \mathcal{L}_2=\left( \stackrel{\color{red}{H}}{\color{red}{0.065}} ,\quad \stackrel{\color{blue}{C}}{\color{blue}{0.0058}} \right) ,\quad P= \stackrel{H\quad C}{% \begin{bmatrix} 0.6 & 0.4 \\ 0.3 & 0.7 \end{bmatrix}% },\quad E= \begin{matrix} H \\C \end{matrix} \stackrel{G\quad \color{orange}{W}\quad M}{% \begin{bmatrix} 0.6 & 0.3 & 0.1 \\ 0.2 & 0.4 & 0.4 \end{bmatrix}% } \end{split}\]

  • Probabilidad de la cadena \(H-H-H\)

\[ \mathcal{L}_2(H)\cdot P(H\rightarrow H)\cdot E(H\rightarrow M) = 0.065\times 0.6 \times 0.1 = 0.0039 \]

  • Probabilidad de la cadena \(H-H-C\)

\[ \mathcal{L}_2(H)\cdot P(H\rightarrow C)\cdot E(C\rightarrow M) = 0.065\times 0.4 \times 0.4 = 0.0104 \]

  • Probabilidad de la cadena \(H-C-H\)

\[ \mathcal{L}_2(C)\cdot P(C\rightarrow H)\cdot E(H\rightarrow M) = 0.058 \times 0.3 \times 0.1 = 0.00174 \]

  • Probabilidad de la cadena \(H-C-C\)

\[ \mathcal{L}_2(C)\cdot P(C\rightarrow C)\cdot E(C\rightarrow M) = 0.058\times 0.7\times 0.4 = 0.01624 \]
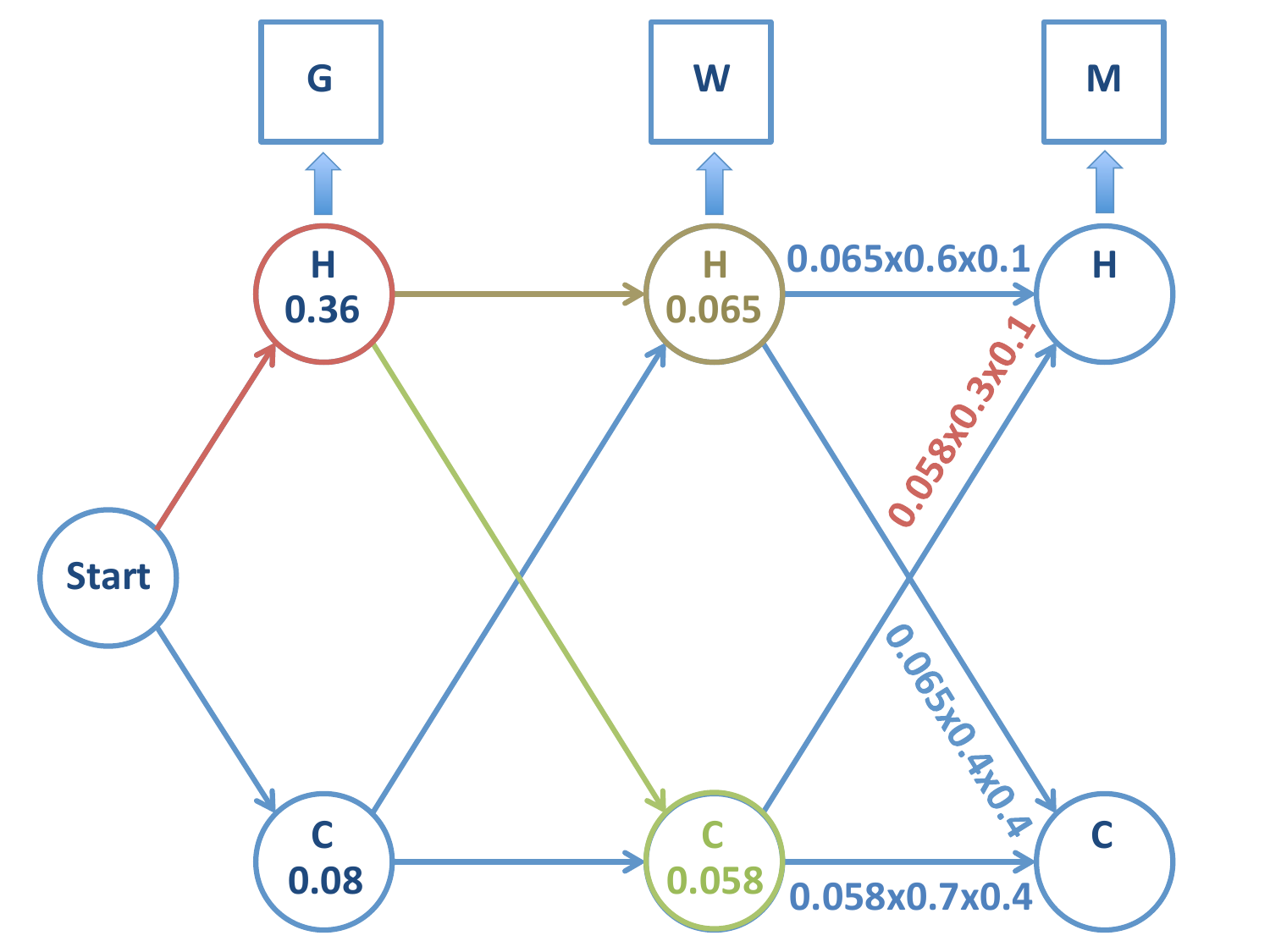
_images/hmm5.png

Fig. 17 Viterbi

Observaciones

  • De los dos caminos que llegan a \(H\) en la tercera etapa, el más probable es el que viene de \(C\), por tanto descartamos el camino \(H-H-H\).

  • De los dos caminos que llegan a \(C\) en la tercera etapa, el más probable es el que proviene de \(C\) en la segunda. Descartamos el camino \(H-H-C\).

  • Las dos observaciones anteriores hacen que descartemos el estado \(H\) en la segunda etapa. Esto no es trivial, pues si hubiésemos detenido el proceso en dicha etapa, el último estado más probable hubiera sido \(H\)!

  • Los dos posibles caminos son

    • \(H-C-H\) con una probabilidad de 0.001728

    • \(H-C-C\) con una probabilidad de 0.0161

El último estado es el de mayor verosimilitud: \(H-C-C\).

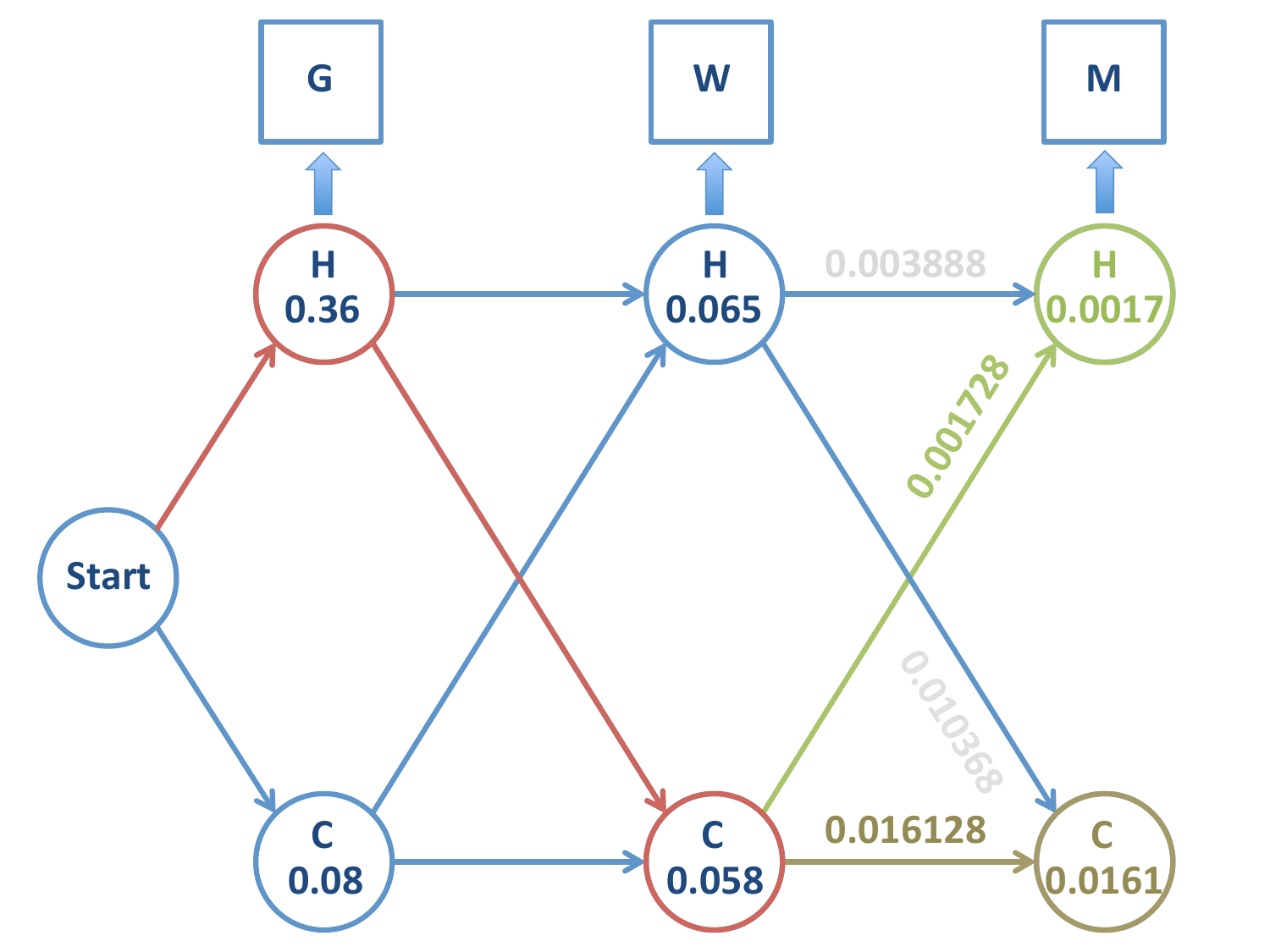
_images/hmm6.png

Fig. 18 Viterbi

previous

4.4 Modelos de Markov Ocultos

next

4.6 Práctica 1: cadenas de Markov como Modelos de Secuencias