Contents

4.2 Comportamiento asintótico

Estamos interesados en conocer cómo es el vector \(\pi^{(n)}\) para \(n\) grande, y cómo está relacionada con \(P^{(n)}\).

Si conocemos el vector de probabilidades inicial \(\pi^{(0)}\) podemos simular el comportamiento.

Pregunta: ¿Por qué es importante conocer el \(\pi^{(n)}\) para \(n\) grande?

  • Ejemplo del tiempo

  • Ejemplo de la pulga

  • Ejemplo de los conductores $\( \text{Precio del seguro}=f_d*C*\mathbb{P}(L) \)$

  • Ejemplo de la ruina del apostador

Ejemplo: el tiempo en mi ciudad

Tomemos el ejemplo El tiempo en mi ciudad donde la matriz de transición es:

\[\begin{split} P =\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix} \end{split}\]

Si partimos de un día que llueve, es decir, \(\pi^{(0)}=(1,0)\) entonces los sucesivos estados de la cadena son

\[ \pi^{(n)}=\pi^{(0)}\cdot P^n,\quad n=1,2,\ldots \]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = np.array((1,0))
P = np.array([[3/5, 2/5], [1/5, 4/5]])
print('Sumas de filas: ',P.sum(axis=1))
iteraciones = np.arange(20)
columns = ['P(lluvia)','P(sol)']
res = pd.DataFrame(index = iteraciones, columns=columns)
res.loc[0] = x
for ii in iteraciones:
    x = x.dot(P)
    res.loc[ii+1] = x
f,ax = plt.subplots(nrows=1,ncols=1,figsize=(8,8))
xx = res.index
for c in columns:
    yy = res[c]
    ax.plot(xx,yy,'.--',label=c,markersize=10)
ax.legend()
res.head(10)

Sumas de filas:  [1. 1.]
P(lluvia) P(sol)
0 1 0
1 0.6 0.4
2 0.44 0.56
3 0.376 0.624
4 0.3504 0.6496
5 0.34016 0.65984
6 0.336064 0.663936
7 0.334426 0.665574
8 0.33377 0.66623
9 0.333508 0.666492
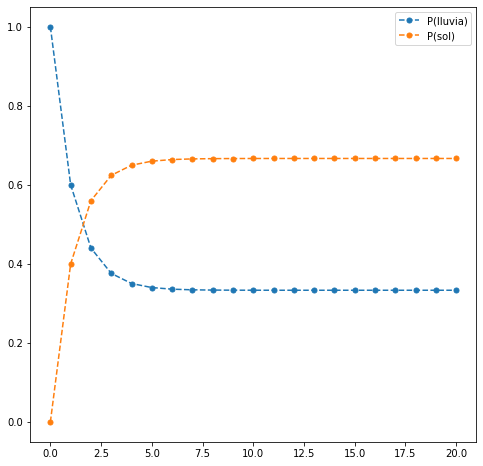
_images/04.02B_CadenasMarkovAsintotico_1_2.png

Observación: Se puede comprobar que la convergencia, en este caso, no depende del estado inicial.

Haremos solamente una prueba con otro estado inicial.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = np.array((0,1))
P = np.array([[3/5, 2/5], [1/5, 4/5]])
print('Sumas de filas: ',P.sum(axis=1))
iteraciones = np.arange(20)
columns = ['P(lluvia)','P(sol)']
res = pd.DataFrame(index = iteraciones, columns=columns)
res.loc[0] = x
for ii in iteraciones:
    x = x.dot(P)
    res.loc[ii+1] = x
f,ax = plt.subplots(nrows=1,ncols=1,figsize=(8,8))
xx = res.index
for c in columns:
    yy = res[c]
    ax.plot(xx,yy,'.--',label=c,markersize=10)
ax.legend()
res.head(10)

Sumas de filas:  [1. 1.]
P(lluvia) P(sol)
0 0 1
1 0.2 0.8
2 0.28 0.72
3 0.312 0.688
4 0.3248 0.6752
5 0.32992 0.67008
6 0.331968 0.668032
7 0.332787 0.667213
8 0.333115 0.666885
9 0.333246 0.666754
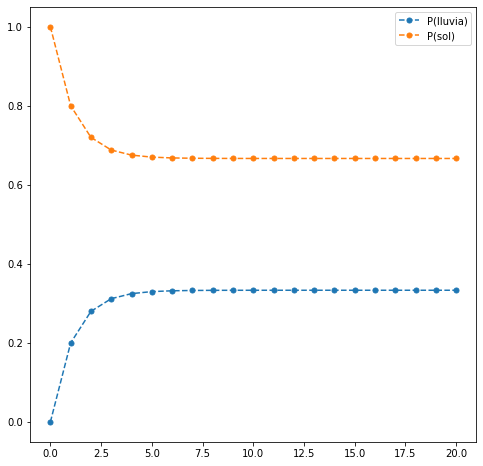
_images/04.02B_CadenasMarkovAsintotico_3_2.png

Ejemplo sin límite

Veamos un caso diferente. Sea una cadena de Markov con matriz de transiciones

\[\begin{split} P=\begin{pmatrix}0&1\\1&0\end{pmatrix}, \end{split}\]

y vector de estados inicial \(\pi^{(0)}=(1,0)\) entonces la evolución de los vectores de estados es la siguiente:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = np.array((1,0))
P = np.array([[0, 1], [1, 0]])
print('Sumas de filas: ',P.sum(axis=1))
iteraciones = np.arange(20)
columns = ['E1','E2']
res = pd.DataFrame(index = iteraciones, columns=columns)
res.loc[0] = x
for ii in iteraciones:
    x = x.dot(P)
    res.loc[ii+1] = x
f,ax = plt.subplots(nrows=1,ncols=1,figsize=(8,8))
xx = res.index
for c in columns:
    yy = res[c]
    ax.plot(xx,yy,'.--',label=c,markersize=10)
ax.legend()
res.head(10)

Sumas de filas:  [1 1]
E1 E2
0 1 0
1 0 1
2 1 0
3 0 1
4 1 0
5 0 1
6 1 0
7 0 1
8 1 0
9 0 1
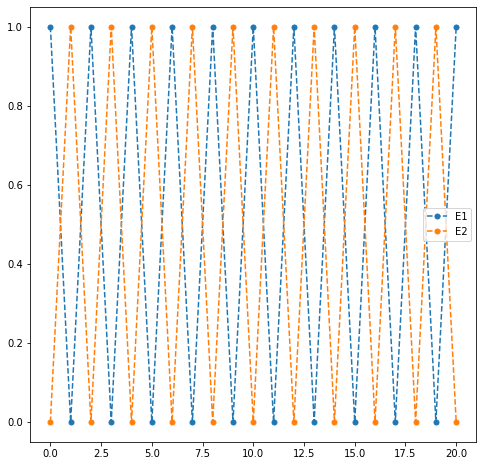
_images/04.02B_CadenasMarkovAsintotico_5_2.png

En cambio, si empezamos desde otro vector de probabilidades inicial \(\pi^{(0)}=(1/2,1/2)\)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = np.array((1/2,1/2))
P = np.array([[0, 1], [1, 0]])
print('Sumas de filas: ',P.sum(axis=1))
iteraciones = np.arange(20)
columns = ['E1','E2']
res = pd.DataFrame(index = iteraciones, columns=columns)
res.loc[0] = x
for ii in iteraciones:
    x = x.dot(P)
    res.loc[ii+1] = x
f,ax = plt.subplots(nrows=1,ncols=1,figsize=(8,8))
xx = res.index
for c in columns:
    yy = res[c]
    ax.plot(xx,yy,'.--',label=c,markersize=10)
ax.legend()
res.head(10)

Sumas de filas:  [1 1]
E1 E2
0 0.5 0.5
1 0.5 0.5
2 0.5 0.5
3 0.5 0.5
4 0.5 0.5
5 0.5 0.5
6 0.5 0.5
7 0.5 0.5
8 0.5 0.5
9 0.5 0.5
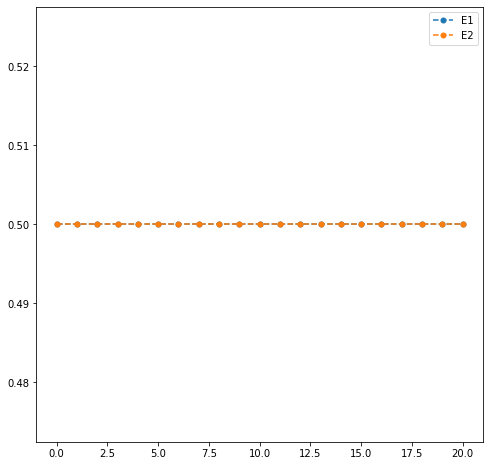
_images/04.02B_CadenasMarkovAsintotico_7_2.png

Distribución asintótica

Se dice que \(\lambda =(\lambda_1,\ldots,\lambda_r)\), con \(\lambda_i\geq 0\) y \(\sum_{i}\lambda_i=1\) es una distribución asintótica de la cadena de Markov si

\[ \lambda = \lim_{n\to\infty} \pi^{(n)} = \lim_{n\to\infty}\pi^{(0)}P^n, \]

para cualquier \(\pi^{(0)}\) inicial.

Hemos visto que esta distribución no tiene por qué existir, pero cuando lo hace se puede calcular como

\[ \lambda_j=\lim_{n\to\infty}(P^n)_{ij},\quad \forall j. \]

En otras palabras, sucede que

\[\begin{split} P^n\xrightarrow[n\to\infty]{}\begin{pmatrix}\lambda_1&\cdots&\lambda_r\\ \lambda_1&\cdots&\lambda_r\\ \vdots & \ddots & \vdots\\ \lambda_1&\cdots&\lambda_r\end{pmatrix} \end{split}\]

Pregunta: ¿qué sucede en el caso de las matrices anteriores?

Caso

\[\begin{split} P =\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix} \end{split}\]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Pt = np.array([[3/5, 2/5], [1/5, 4/5]])
P = Pt.copy()
ptt = list(P.ravel())
iteraciones = 20
for _ in np.arange(iteraciones):
    P = P.dot(Pt)
    ptt+=(list(P.ravel()))

f,ax = plt.subplots(nrows=1,ncols=1,figsize=(8,8))
for i in np.arange(4):
    els = [xx for ii,xx in enumerate(ptt) if ii%4==i]
    plt.plot(els,'.--',label='Elemento: {}, len: {}'.format(i,len(els)),alpha=0.5)
ax.legend()

<matplotlib.legend.Legend at 0x7f4185ef5a00>
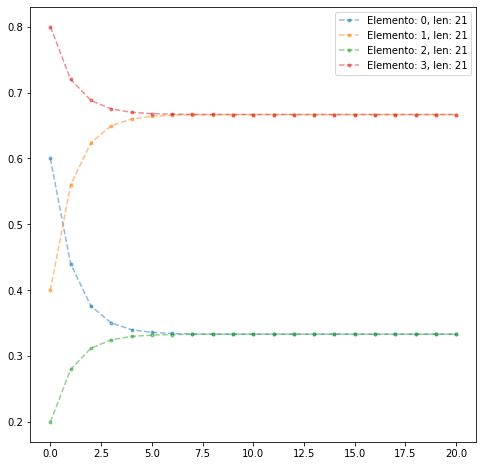
_images/04.02B_CadenasMarkovAsintotico_10_1.png

Caso

\[\begin{split} P=\begin{pmatrix}0&1\\1&0\end{pmatrix} \end{split}\]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Pt = np.array([[0, 1], [1, 0]])
P = Pt.copy()
ptt = list(P.ravel())
iteraciones = 20
for _ in np.arange(iteraciones):
    P = P.dot(Pt)
    ptt+=(list(P.ravel()))

f,ax = plt.subplots(nrows=1,ncols=1,figsize=(8,8))
for i in np.arange(4):
    els = [xx for ii,xx in enumerate(ptt) if ii%4==i]
    plt.plot(els,'.--',label='Elemento: {}, len: {}'.format(i,len(els)),alpha=0.5)
ax.legend()

<matplotlib.legend.Legend at 0x7f4185fed3d0>
_images/04.02B_CadenasMarkovAsintotico_12_1.png

¿Qué sucede si empezamos en la distribución límite? Es decir

\[ \pi^{(0)}=\lambda\quad \text{¿ }\pi^{(1)}\text{ ?} \]

Escogemos cualquier \(i\) y tenemos

\[ \pi^{(1)}=\lambda P= \left(\lim_{n\to\infty}P^n_{i,\cdot}\right)P= \left(\lim_{n\to\infty}P_{i,\cdot}^{n+1}\right)= \lambda. \]

Distribución estacionaria

Note

Si empezamos en la distribución límite, estaremos allí para siempre. Esto motiva la siguiente definición

Definition 1 (Distribución estacionaria)

Dada una cadena de Markov con matriz de transición \(P\), una distribución estacionaria es una distribución de probabilidad \(\pi\) que satisface

\[ \pi=\pi P \Leftrightarrow \pi_j=\sum_{i}\pi_i P_{ij},\quad \forall j. \]

Si empezamos la cadena de Markov en la distribución estacionaria \(\pi\), la distribución no cambiará: estacionaria.

Otros nombres que recibe esta distribución:

  • medida o distribución invariante

  • probabilidad o distribución de equilibrio (física)

Relación entre distribución estacionaria y distribución límite

Recordatorio

Queremos conocer la distribución límite, pero es mucho más sencillo calcular la distribución estacionaria resolviendo el Sistema de Ecuaciones Lineales (SEL) anterior.

Las preguntas que nos podemos hacer son:

i) Existe?

ii) Es única?

iii) Cuándo la distribución de equilibrio es una distribución límite? Es decir, cuándo, partiendo de una distribución inicial \(\pi^{(0)}\) cualquiera, la cadena de Markov converge a ella?

Observación

Hemos visto que ser una distribución límite implica ser una distribución estacionaria, pero la implicación inversa no es cierta (ver ejemplo Ejemplo sin límite) con las distribuciones iniciales \(\pi^{(0)}=(0.5, 0.5)\) y \(\pi^{(0)}=(1, 0)\).

Queremos saber, bajo qué condiciones una distribución estacionaria será la distribución límite. Para ello necesitamos las siguientes definiciones

Definition 2 (Matriz positiva)

Decimos que una matriz \(A=(a_{ij})\) es positiva si \(a_{ij}>0\) para todo \(i,j\).

Definition 3 (Matriz regular)

Una matriz \(P\) estocástica es regular si existe algún \(s>0\) tal que \(P^s\) es positiva, es decir

\[ (P^s)_{ij}>0,\quad \forall i,j. \]

Si la matriz de transiciones de una cadena de Markov es regular decimos que la cadena de Markov es regular.

Esto quiere decir que, para un tiempo \(s\), se puede siempre llegar desde cualquier estado a cualquier otro estado de la cadena de Markov.

Entonces tenemos el siguiente teorema

Theorem 3 (Comportamiento asintótico)

Sea una cadena de Markov regular, con \(|\mathcal{X}|=r<\infty\). Entonces existe una única distribución de probabilidad estacionaria \(\pi=(\pi_1,\ldots,\pi_r)\) con \(\pi_i>0\) para todo \(i\).

Además, el vector de probabilidad a tiempo \(n\), \(\pi^{(n)}\) converge a \(\pi\), es decir

\[ \lim_{n\to\infty}P^n_{ij}=\pi_j,\quad \forall i. \]

Cálculo de distribución estacionaria

Ejemplo del clima

La matriz de transiciones es obviamente regular. Luego el vector de equilibrio satisface el sistema:

\[\begin{split} (\pi_1\quad \pi_2)\begin{pmatrix}\frac{3}{5}&\frac{2}{5}\\\frac{1}{5}&\frac{4}{5}\end{pmatrix}= (\pi_1\quad \pi_2) \end{split}\]

Es una ecuación de autovectores: es siempre un sistema compatible indeterminado. Lo resolvemos eliminando una de las ecuaciones:

\[ \frac{3}{5}\pi_1+\frac{1}{5}\pi_2=\pi_1,\quad \frac{1}{5}\pi_2=\frac{2}{5}\pi_1,\quad \pi_2=2\pi_1.\]

Hay infinitas soluciones, pero tenemos otra ecuación que podemos añadir al sistema:

\[ \pi_1+\pi_2=1, \]

debido a que se trata de un vector de probabilidad. Por tanto:

\[ \pi=\left(\frac{1}{3},\quad \frac{2}{3}\right). \]

previous

4.2 Cadenas de Markov

next

4.3 Cadenas de Markov como modelos de secuencias