import numpy as np
Robbie el Robot Recogebasura¶
Este ejemplo proviene del libro [Mitchell, 2009] de Melanie Mitchell.
El capítulo 9 aquí.
Presentación¶
Mundo bidimensional: mallado de \(10\times10\) celdas
Robot Robbie
Celdas con/sin lata/basura (con probabilidad)
Recinto cerrado con pared
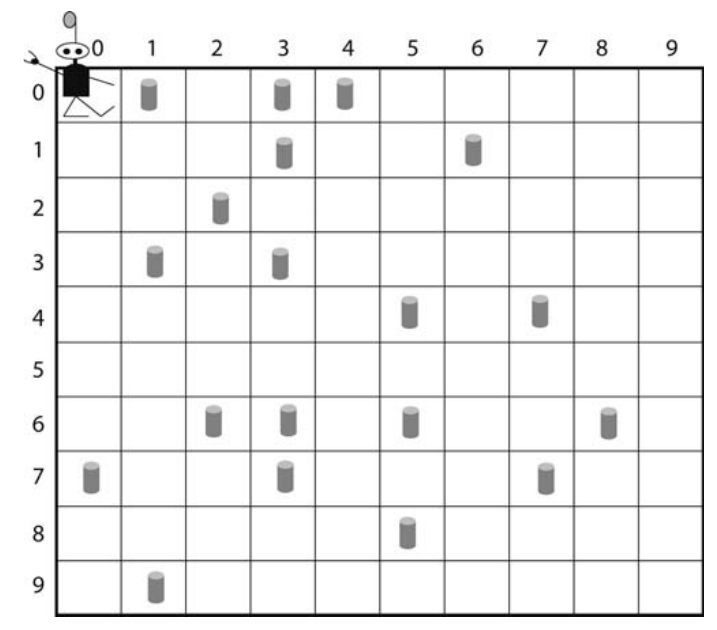
Robbie es un robot que puede
ver lo que sucede en las celdas inmediatamente adyacentes (N,S,E,O)
ver lo que sucede en su celda
recoger lo que hay en su celda
moverse (N,S,E,O)
Sesión de limpieza¶
Cada sesión lleva 200 acciones de Robbie (recoger, moverse)
Cada acción tiene un premio o castigo
Si Robbie está en un sitio con basura y la recoge: premio = 10 puntos
Si Robbie se agacha a recoger basura y no hay: castigo = 1 punto
Si Robbie se choca con una pared: castigo = 5 puntos (y rebota al sitio donde estaba)
Objetivo: maximizar el premio de Robbie \(\sim\) limpiar lo más posible el recinto sin chocarse ni agacharse a recoger cuando no hay basura.
¿Podemos pensar en una estrategia para limpiar el recinto de la manera más eficiente posible?
Estrategias¶
Vamos a dejar que el ordenador evolucione una estrategia para Robbie
¿Estrategia?
Conjunto de normas: para cada posible situación, la acción a tomar
¿Situación?: lo que Robbie puede ver (su posición y sus vecinos)
¿Acción a tomar?: elegir entre las 7 posibles acciones
Moverse (N,S,E,O, random)
Quedarse quieto
Recoger lata
Ejemplo de una situación y una acción
| Situation || Action | |——-|——-|——|——|———|———–|
North |
South |
East |
West |
Current |
|
|---|---|---|---|---|---|
Wall |
Empty |
Can |
Wall |
Empty |
Move West |
Robbie tiene una tabla con todas las posibles situaciones y las acciones a tomar en cada situación.
La estrategia anterior no es una buena estrategia, pero es una estrategia
Posibles situaciones: hay 243 situaciones posibles (como máximo). La lista debe contener al menos ese número de entradas.
Algoritmo Genético¶
Población: cada individuo es una estrategia: un listado de las acciones a seguir por Robbie en cada una de las 243 posibles situaciones.
Por ejemplo, un individuo/estrategia es:
MoveNorth MoveEast MoveRandom PickUpCan … MoveWest … StayPut
Las acciones están listadas siempre en el mismo orden, por lo tanto Robbie es capaz de reconocer la acción a tomar por su posición en la lista (situación).
No es necesario poner la lista de todas las situaciones una y otra vez: con las acciones basta.
Fases¶
Población inicial: 200 estrategias/individuos aleatorias

Cada estrategia individual es una lista de 243 genes
Cada gen es un número entre 0 y 6.
0: MoveNorth
1: MoveSouth
…
6: RandomMove
Repetir para \(N=1000\) generaciones
Calcular el fitness de cada individuo en la población
Realizar 100 sesiones de limpieza con Robbie para cada estrategia
Robbie empieza en la posición (0,0)
Se colocan latas aleatoriamente en el mallado (cada sitio puede tener a lo sumo una lata)
La probabilidad de contener una lata es del 50%
Cada sesión de limpieza son 200 acciones de Robbie
Al final de la sesión se anota el puntaje de Robbie
El fitness de la estrategia es la media de los puntajes para las 100 sesiones
Evolución
Crear una nueva población a partir de la ya existente
Repetir hasta obtener una población con \(200\) individuos:
(a) Elegir dos individuos (padres) de la población actual probabilísticamente basándose en el fitness
a mayor fitness, mayor probabilidad de ser elegidos
(b) Crear un hijo a partir de los dos padres
elegir una posición aleatoria, \(p\), para partir las dos cadenas de genes
formar un hijo tomando la cadena del padre \(A\) hasta \(p\) y la cadena del padre \(B\) desde \(p\)
viceversa para formar un segundo hijo
(c) Mutar números de los hijos formados: con una probabilidad dada (pequeña), elegir uno o más números de la cadena de los hijos y reemplazarlos por un número aleatorio entre el 0 y el 6
(d) Incluír los hijos en la población
Repetir desde el paso 2.
Fitness score¶
Si en cada sesión de limpieza (simulación) cada espacio tiene un \(50\%\) de probabilidad de contener una lata, por tanto, aproximadamente el \(50\%\) de los sitios tendrán una lata, es decir, habrá de media 50 latas en el recinto.
El máximo score posible es aproximadamente 500.
Estrategia propia¶
Compararemos el resultado del GA con una estrategia inteligente:
Si hay una lata en el sitio actual: recógela
Si hay una lata en un sitio adyacente, muévete al sitio adyacente
Si hay latas en varios sitios adyacentes, se especifica a qué sitio va
Si no hay latas a la vista, moverse aleatoriamente
¿Problemas?
Testado en \(10^4\) sesiones de limpieza: fitness score: 346 (lejos del óptimo).
Algoritmo genético¶
Después de correr el algoritmo, seleccionamos el individuo con mayor fitness de la última generación. Testado en \(10^4\) sesiones de limpieza. El fitness score (medio) es de 483.
casi óptimo
mucho mayor que la estrategia inteligente
Genomas¶
M: estrategia inteligente
G: estrategia GA evolucionada
M: 65635365625235325265635365615135315125235325215135315165635365 62523532526563536560503530502523532520503530501513531512523532 5215135315105035305025235325205035305065635356252353252656353 656151353151252353252151353151656353656252353252656353454
G: 25435515325623525105635546115133615415103415611055015005203025 62561322523503251120523330540552312550513361541506652641502665 06012264453605631520256431054354632404350334153250253251352352 045150130156213436252353223135051260513356201524514343432
No es muy informativo
En algunos casos vemos que coincide y tiene sentido:
Posición 2: “Empty Empty Empty Empty Can”
Acción: 5 - recoger lata
Pero en este tipo de situaciones no siempre coinciden las estrategias:
North |
South |
East |
West |
Current |
|---|---|---|---|---|
Empty |
Can |
Empty |
Can |
Can |
La estrategia inteligente determina: acción 5 - recoger lata
La estrategia \(G\) determina: acción 3 - MoveWest
Robbie no recoge la lata!
Parece una mala idea
Pero \(G\) tiene mejor fitness
No se trata del efecto de genes aislados, si no de la interacción entre ellos (igual que en genética)
¿Cómo afecta al fitness global la interacción?
Nos fijamos en el Fenotipo: comportamiento de Robbie en cada estrategia
Nos fijamos en dos cambios visibles entre los comportamientos
Movimiento con pocas latas¶
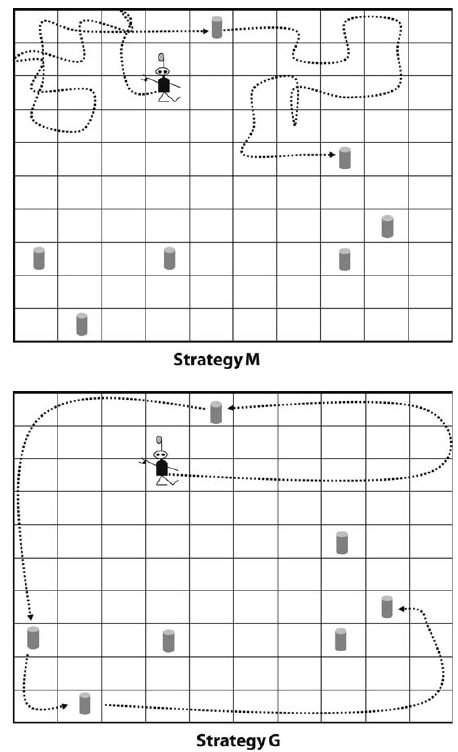
Fig. 41 Comportamiento de Robbie en una situación en la que hay pocas latas¶
En la gráfica anterior vemos cómo actúa Robbie cuando hay pocas latas en el espacio. Cuando Robbie no detecta una lata en su espacio, ni en espacios adyacentes, las estrategias indican:
M: movimiento aleatorio
G: MoveEast hasta encontrar una lata o una pared. Después se mueve al Norte y rodea el borde de modo antihorario hasta que encuentra una lata (ver figura).
Esta estrategia previene que Robbie se choque con una pared (reducción del fitness), que sí es posible con M, pero además es más eficiente a la hora de encontrar latas que simplemente moviéndose de forma aleatoria.
Estrategia con varias latas¶
Situación de la figura (arriba izquierda): Robbie se encuentra en una posición en la que hay una lata y también hay latas en las posiciones vecinas (este y oeste)
M: coge lata, mueve oeste, coge lata. Entonces Robbie ya no ve más latas y comienza a moverse aleatoriamente hasta que se encuentre una lata.
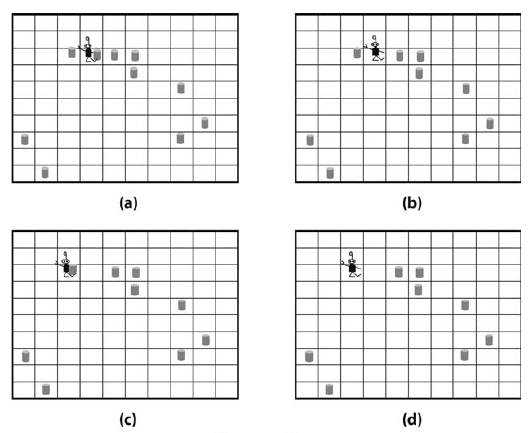
Fig. 42 Cluster de latas: estrategia M¶
G: NO coge la lata, si no que se mueve al oeste. Coge lata. La lata que no cogió en el paso anterior es un marcador que le recuerda que hay más latas al otro lado. Después continúa cogiendo todas las latas del cluster.
Robbie coge primero la lata que se encuetra más al oeste
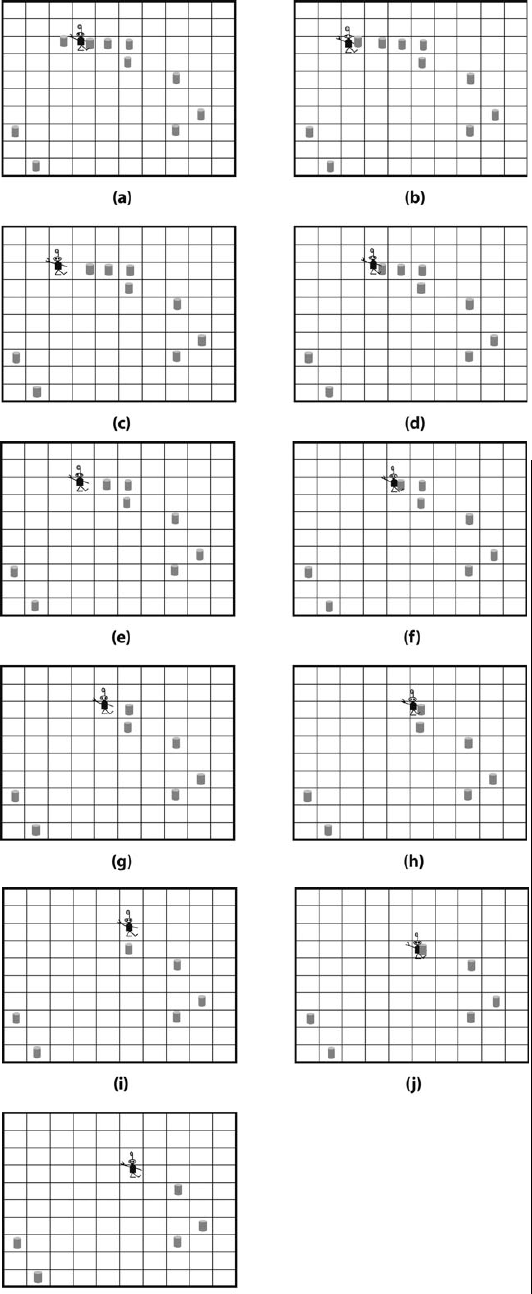
Fig. 43 Cluster de latas: estrategia G¶
Melanie no consideró este truco cuando programó su algoritmo
Los GA suelen llegar a estrategias que no se nos ocurren
Estrategia knock-out (genética, eliminar genes para ver su funcionalidad)
Melanie eliminó los genes que responsables de este comportamiento en la estrategia G, el fitness descendió de 483 a 443: este truco es, en parte, responsable del éxito de G
Evolución del fitness¶
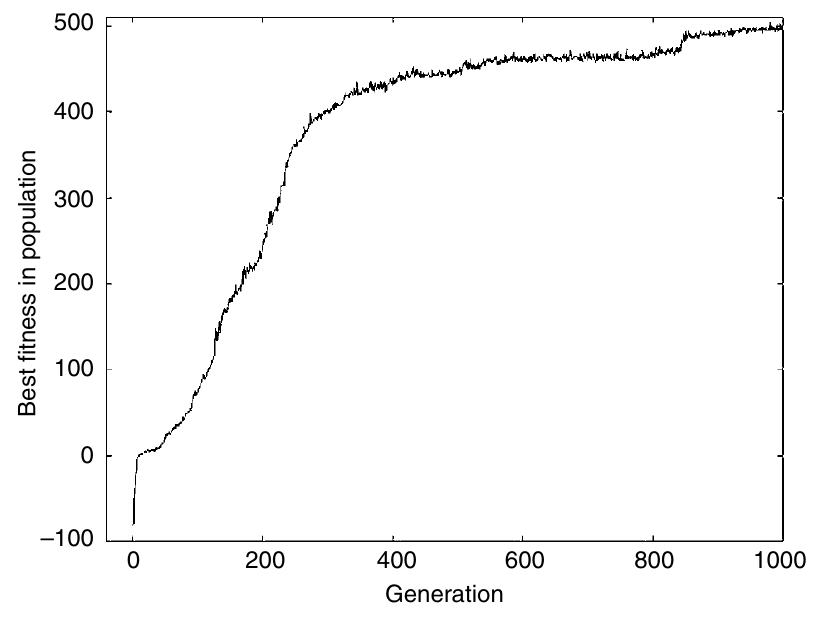
Fig. 44 Evolución del fitness¶
Las primeras estrategias son muy malas
Algunas consisten en Robbie estrellándose repetidamente con una pared
Otras Robbie se queda quieto todo el rato
La selección de la mejor hace que se avance rápidamente
Hay un incremento rápido
Las estrategias muy malas desaparecen
Alrededor de la generación 200 ya se han descubierto buenos traits (moverse y recoger)
No obstante, cuando no hay muchas latas, no sabe cómo buscarlas (como estrategia M)
Y una estabilización
Alrededor de la generación 800 ya se ha descubierto el truco de dejar latas como marcadores
Por la generación 900 se descubre el truco de moverse en círculos (\(\sim1000\))
Aplicaciones reales¶
Los algoritmos genéticos evolucionan a soluciones que funcionan
Es difícil ver por qué funcionan
Son soluciones diferentes de las que ideamos los humanos
Note
“Evolutionary algorithms are a great tool for exploring the dark corners of design space. You show [your designs] to people with 25 years’ experience in the industry and they say ‘Wow, does that really work?’…. We frequently see evolved designs that are completely unintelligible.”
Jason Lohn (NASA)
Caso Evolved Antenna

Fig. 45 Evolución de la forma de una antena (NASA)¶
