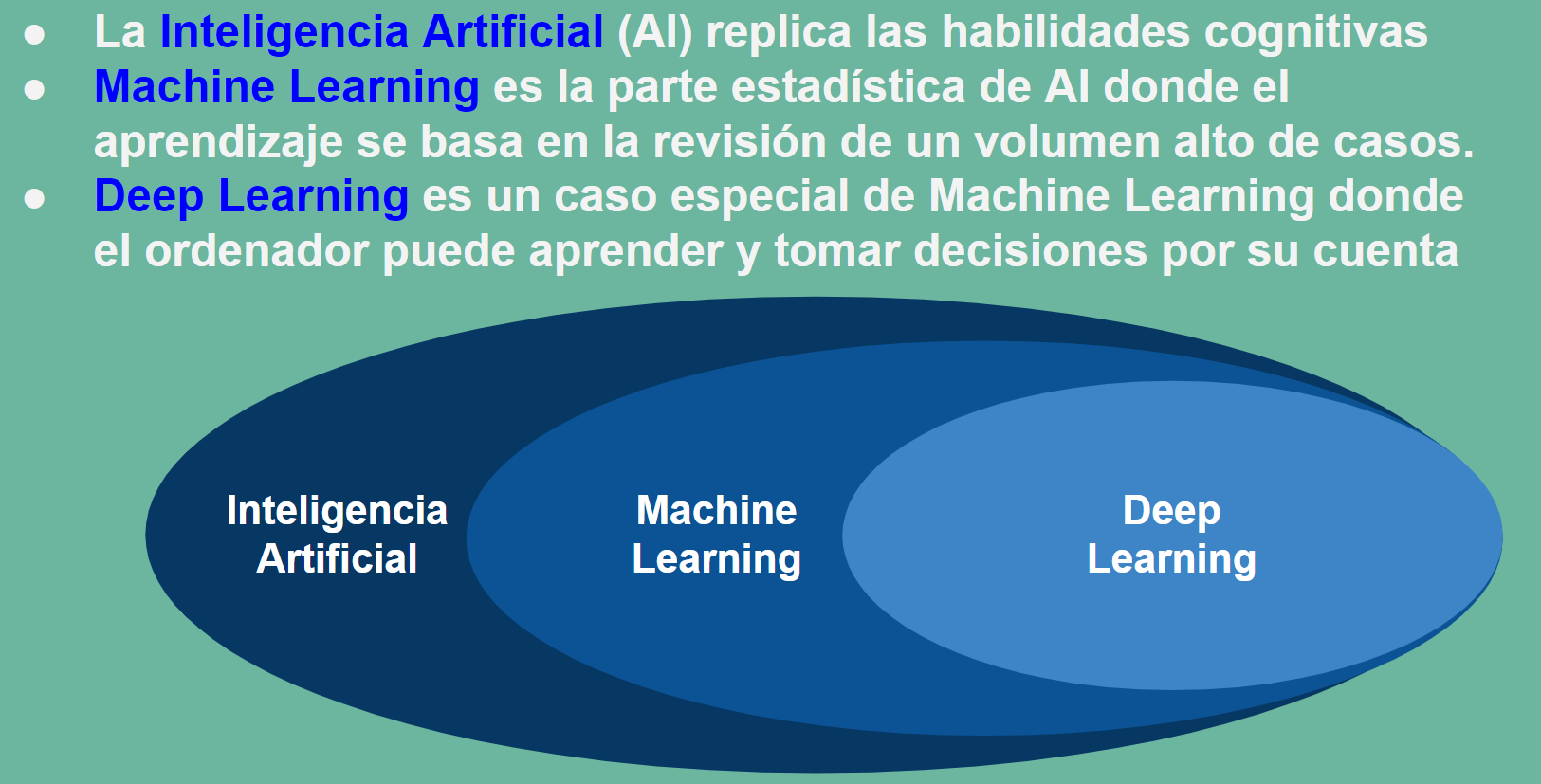
01 Introducción al Aprendizaje Automático¶

import matplotlib.pyplot as plt 
%matplotlib inline
import pandas as pd
import numpy as np
from skimage import io
from IPython import display

La asignatura de Aprendizaje Automático es un compendio de nuevas técnicas de análisis de datos avanzados que de la mano de la estadística y de los avances de la programación han abierto un nuevo horizonte en campos hasta ese momento vedados al análisis.

Uno de esos campos es sin lugar a duda los campos de la biología, que por la complejidad de sus modelos se encontraba fuera de muchos de los avances que la física matemática había aplicado a otros campos de la ingeniería como la electrotecnia y electrónica, la termodinámica o la mecánica de materiales por ejemplo.

Pero incluso los modelos informáticos inspirados en procesos biológicos se han constituido en herramientas de propósito general para construir los esquemas de trabajo, caso de las redes neuronales, o resolver problemas generales, caso de la aplicación de los algoritmos genéticos a la solución de problemas generales de optimización.

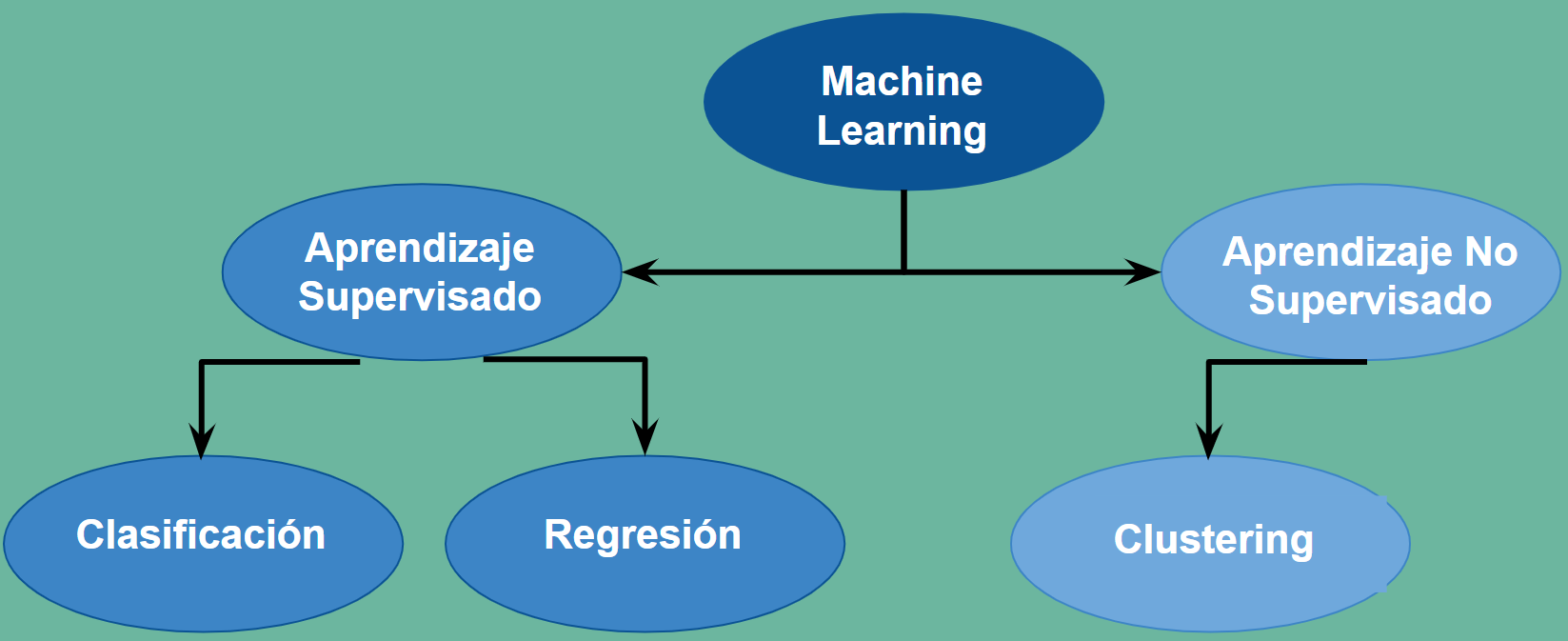
Aprendizaje supevisado vs no supevisado. Regresión vs Clasificación¶

El Aprendizaje Automático hace referencia a la preparación de un modelo entrenado estadisticamente donde se correlacionan unas observaciones, llamadas $X$ con una variable objetivo llamada $Y$. Durante el entrenamiento se construye un modelo que relaciona las observaciones recogidas en el conjunto $X$ con la variable recogida en el conjunto $Y$, que son observaciones reales conocidas de antemano.

Una vez ajustado el modelo servirá para predecir valores $Y$, objetivos desconocidos, sobre un conjunto de nuevas observaciones $X$. Esto es lo que se denomina aprendizaje supervisado, porque en el entrenamiento el disponer de objetivos conocidos $Y$ de unas observaciones $X$ permite supervisar el entrenamiento.

Finalmente hay casos en que ni siquiera conocemos ninguna variable objetivo. Simplemente nos piden que establezcamos una clasificación, (buena, regular, mala) por ejemplo, sobre un conjunto de observaciones de las que no tenemos experiencia previa. En estos casos estaremos hablando de aprendizaje no supervisado. Se aplicarán métodos que permiten hacer clasificaciones genéricas no condicionadas por una experiencia previa.

En el aprendizaje supervisado podemos encontrarnos con que los valores $Y$ sean continuos, cualquier valor de los números reales. En este caso los métodos supervisados a aplicar son las Regresiones. Mientras que si $Y$ toma sólo un conjunto discreto de valores, supongamos $ \{0, 1, 2, ..., k\} $ hablamos de métodos de Clasificación. Resumiendo una primera clasificación del Aprendizaje Automático puede ser:

Aprendizaje Supervisado. Cuando el modelo se ajusta a partir de valores conocidos $X$ e $Y$
- Regresiones. Cuando los valores que toman $Y$ son continuos
- Clasificaciones. Cuando los valores que toman $Y$ son discretos
Aprendizaje no Supervisado. Cuando partimos de valores $X$ para ajustar un modelo.

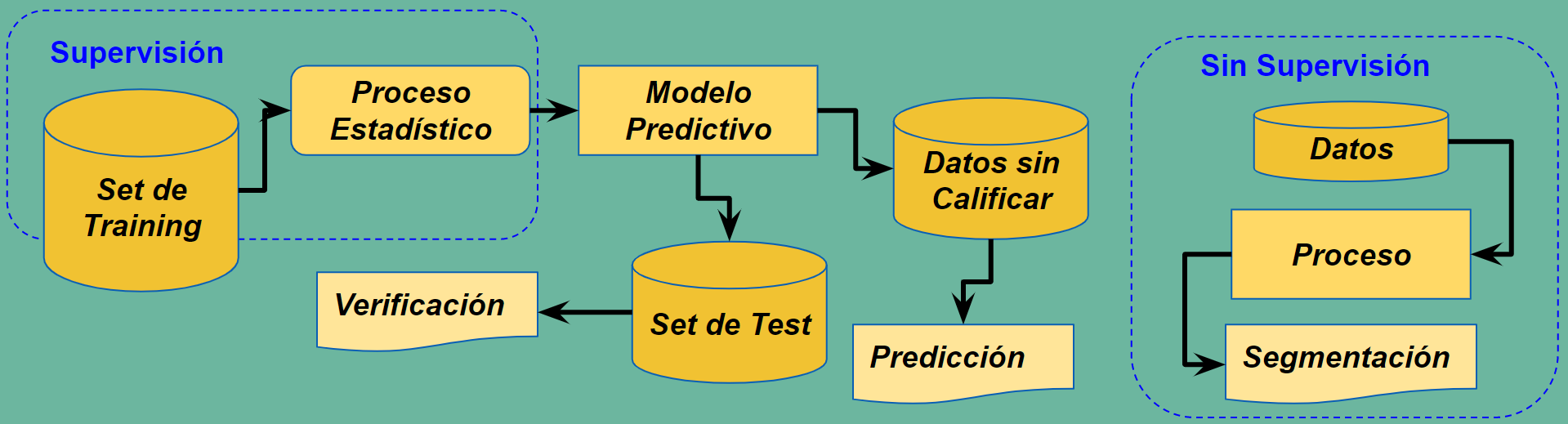
Las matrices $X$ e $Y$¶

Un conjunto de características $X$ se puede definir como una matriz de $N$ filas y $n$ columnas. Las $N$ filas hacen referencia al numero de observaciones registradas o número de individuos de la muestra de partida o entrenamiento. Mientras que $n$ es el número de características observadas y hace referencia a la dimensión de las observaciones. En cada individuo del conjunto recogemos $n$ caracteristicas distintas. Si estamos haciendo un estudio médico sobre 1.000 individuos, $N=1.000$ y si a cada individuo le medimos la presión arterial, el nivel de glucosa y el nivel de colesterol, $n=3$. Podremos recoger los datos de nuestro conjunto de entrenamiento en una matriz $1.000 \times 3$.

\[\begin{split}X=\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1n} \\ x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N1} & x_{N2} & \cdots & x_{Nn} \\ \end{bmatrix}\end{split}\]

Si el estudio médico es un modelo supervisado las variables objetivo $Y$ que permiten entrenar el modelo se pueden definir como una matriz columna de $N$ filas o una matriz $N \times 1$

\[\begin{split}Y=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \\ \end{bmatrix}\end{split}\]

Los conjuntos de entrenamiento y validación, train y test, en el aprendizaje automático¶

El ajuste del modelo estadistico de un método supervisado se realiza sobre una parte de los conjuntos $X$ e $Y$ de partida. Se hace una partición tanto de $X$ como de $Y$ en dos subconjuntos. El primero, que se denomina de entranamiento o train se utiliza para hacer realmente el ajuste del modelo. Y este ajuste se valida en el subconjunto que se ha reservado a tal fin y al que se da el nombre de conjunto de test o validación.

Esto es así porque los métodos de ajuste pueden conseguir una convergencia sobre el conjunto de entrenamiento que sea ficticia, lo que se llama sobreajuste, y luego al validar se comprueba que el ratio de éxito es muchísimo menor. Esto puede ser así porque realmente el modelo no tenga convergencia o correlación real.

Tratamiento de los Datos¶

Antes de empezar a aplicar ningún método entrenamiento es necesario cargar los datos desde el soporte de archivos o base de datos donde se encuentren. Aquí se cargarán desde archivos que se esperan en la carpeta data utilizando la librería Pandas.

Una vez cargado es necesario un proceso de filtrado y depuración para que sea compatible con los procedimientos que se van a aplicar. Así será necesario eliminar valores nulos o convertir valores alfabéticos en númericos.

Gestionar los datos nulos o datos perdidos se puede realizar con diferentes extrategias:

Descartar los registros incompletos.
Imputar un dato por cada valor perdido reemplazando por la media o la mediana.
Imputar en base a una regresión, donde el dato perdido se sustituye por uno predicho.

Además puede surgir la necesidad de transformar los datos:

Estandarización : restando la media $\mu_i$ y dividiendo por la desviación típica $\sigma_i$ en cada una de las $i$ columnas de la matriz $X$ con $i=1,...,n$.
Convertir datos alfabéticos en númericos. Por ejemplo en la matriz $Y$ se sustituyen los nombres de las etiquetas por enteros $0, 1, ..., K$.

Finalmente puede ser de interés hacer un análisis de componentes principales (PCA) en la matriz $X$.

Eliminación de Nulos¶

El archivo breast_cancer_conNulos.csv contiene datos con valores nulos en algunas de sus características. La variable objetivo y es diagnose con valores 0 (benigno, no canceroso) o 1 (maligno, canceroso), respectivamente. El resto de variables son características que constituyen la matriz X.

Realiar lo siguiente:

Cargar con Pandas el archivo.
Evaluar si existen valores nulos o perdidos
Eliminar en Pandar los valores nulos.
Cargar las matrices X e y

Primero se comienza cargando desde la librería Pandas los datos del fichero a un objeto DataFrame. Ésto lo realiza la función read_csv que lee el fichero CSV.

https://pandas.pydata.org/docs/index.html

https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html

Los valores perdidos se pueden detectar y eliminar desde el objeto DataFrame con los métodos isna() y dropnan() respectivamente.

import pandas as pd
df = pd.read_csv('data/breast_cancer_conNulos.csv')
df.head()

	clump_thickness	cell_size_uniformity	cell_shape_uniformity	marginal_adhesion	single_epithelial_cell_size	bare_nuclei	bland_chromatin	normal_nucleoli	mitoses
0	5.0	1.0	1.0	1.0	2.0	1.0	3.0	1.0	1.0
1	5.0	4.0	4.0	5.0	7.0	10.0	3.0	2.0	1.0
2	3.0	1.0	1.0	1.0	2.0	2.0	3.0	1.0	1.0
3	6.0	8.0	8.0	1.0	3.0	4.0	3.0	7.0	1.0
4	4.0	1.0	1.0	3.0	2.0	1.0	3.0	1.0	1.0

Se detectan si existen o no valores perdidos o nulos

Los registros con nulos aparecen arriba y con True.

df.isna()

	clump_thickness	cell_size_uniformity	cell_shape_uniformity	marginal_adhesion	single_epithelial_cell_size	bare_nuclei	bland_chromatin	normal_nucleoli	mitoses	diagnose
0	False	False	False	False	False	False	False	False	False	False
1	False	False	False	False	False	False	False	False	False	False
2	False	False	False	False	False	False	False	False	False	False
3	False	False	False	False	False	False	False	False	False	False
4	False	False	False	False	False	False	False	False	False	False
...	...	...	...	...	...	...	...	...	...	...
683	False	True	True	False	False	True	False	True	True	False
684	True	True	False	False	False	False	False	True	True	False
685	True	False	True	False	False	False	True	False	True	False
686	True	False	False	True	False	False	True	False	True	False
687	False	True	False	False	True	False	False	True	False	False

688 rows × 10 columns

Se borran los valores nulos

df=df.dropna()
df

	clump_thickness	cell_size_uniformity	cell_shape_uniformity	marginal_adhesion	single_epithelial_cell_size	bare_nuclei	bland_chromatin	normal_nucleoli	mitoses	diagnose
0	5.0	1.0	1.0	1.0	2.0	1.0	3.0	1.0	1.0	0
1	5.0	4.0	4.0	5.0	7.0	10.0	3.0	2.0	1.0	0
2	3.0	1.0	1.0	1.0	2.0	2.0	3.0	1.0	1.0	0
3	6.0	8.0	8.0	1.0	3.0	4.0	3.0	7.0	1.0	0
4	4.0	1.0	1.0	3.0	2.0	1.0	3.0	1.0	1.0	0
...	...	...	...	...	...	...	...	...	...	...
678	3.0	1.0	1.0	1.0	3.0	2.0	1.0	1.0	1.0	0
679	2.0	1.0	1.0	1.0	2.0	1.0	1.0	1.0	1.0	0
680	5.0	10.0	10.0	3.0	7.0	3.0	8.0	10.0	2.0	1
681	4.0	8.0	6.0	4.0	3.0	4.0	10.0	6.0	1.0	1
682	4.0	8.0	8.0	5.0	4.0	5.0	10.0	4.0	1.0	1

683 rows × 10 columns

Extraer las matrices X e y

El DataFrame tiene la variable values o el método to_numpy() para volcar la información a un array de doble dimensión.

La matriz X está formada por las 9 primeras columnas y la y es la columna 9. Se pueden extraer por posiciones:

X = df.to_numpy()[:, 0:9]
y = df.to_numpy()[:, 9]
X.shape, y.shape

((683, 9), (683,))

También se puede hacer usando los nombres de las columnas

columnX = df.columns[0:9]
columnY = df.columns[9]
print(columnX, columnY)
X = df[columnX].to_numpy()
#y = df[columnY].to_numpy()
y = df['diagnose'].to_numpy()
X.shape, y.shape

Index(['clump_thickness', 'cell_size_uniformity', 'cell_shape_uniformity',
       'marginal_adhesion', 'single_epithelial_cell_size', 'bare_nuclei',
       'bland_chromatin', 'normal_nucleoli', 'mitoses'],
      dtype='object') diagnose

((683, 9), (683,))

Estandarización de la matriz X¶

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
df_std = pd.DataFrame(X_std, columns = columnX)
df_std.head()

	clump_thickness	cell_size_uniformity	cell_shape_uniformity	marginal_adhesion	single_epithelial_cell_size	bare_nuclei	bland_chromatin	normal_nucleoli	mitoses
0	0.197905	-0.702212	-0.741774	-0.639366	-0.555608	-0.698853	-0.181827	-0.612927	-0.3484
1	0.197905	0.277252	0.262783	0.758032	1.695166	1.772867	-0.181827	-0.285105	-0.3484
2	-0.511643	-0.702212	-0.741774	-0.639366	-0.555608	-0.424217	-0.181827	-0.612927	-0.3484
3	0.552679	1.583204	1.602192	-0.639366	-0.105454	0.125054	-0.181827	1.354008	-0.3484
4	-0.156869	-0.702212	-0.741774	0.059333	-0.555608	-0.698853	-0.181827	-0.612927	-0.3484

Análisis de Componentes Principales¶

El análisis de componentes principales (PCA) ([Jolliffe, 1986]) es una transformación lineal sobre las $n$ componentes de la matriz X. La matriz X está formada por $N$ observaciones $\{x^1, ..., x^N\}$ donde cada observación es un vector de $n$ componentes: $$x^i=(x^i_1, ..., x^i_n)$$

Primero se proyecta los datos contenidos en X sobre un espacio 1-dimensional de base $u_1=(u_{11},...,u_{1n})^T$. Hacemos que el vector sea ortonormal: $u_1^Tu_1=1$

La proyección de cada observación vendrá dada por $u^T_1x^i$ . Y la varianza de los datos proyectados será:

\[\frac{1}{N} \sum^N_{i=1} (u^T_1x^i - u^T_1 \bar{x})^2 = u^T_1 S u_1\]

Donde $\bar{x}=\frac{1}{N} \sum^N_{i=1} x^i$ es el vector media de los datos y $S$ la matriz de covarianza de dimensión $n\times n$

$u_1$ será el primer componente principal si maximiza la varianza:

\[\max\limits_{u_1} u^T_1 S u_1 \; \text{sujeto a} \; u_1^Tu_1=1\]

Optimización de una función de $n$ variables con condición que introduciendo el multiplicador de Lagrange $\lambda_1$ :

\[\max\limits_{u_1} u^T_1 S u_1 + \lambda_1(1 - u_1^Tu_1)\]

Se resuelve derivando con respecto a $u_1$ e igualando a cero:

\[ S u_1=\lambda_1 u_1\]

Esta ecuación indica que $u_1$ y $\lambda_1$ son respectivamente el autovector y autovalor de la matriz de covarianza $S$. Además si premultiplicamos la anterior ecuación por $u^T_1$ se ve que $\lambda_1$ es la varianza:

\[ u^T_1 S u_1=\lambda_1\]

La segunda componente principal $u_2$ será una nueva dirección ortonormal a $u_1$ con la máxima varianza de todas las posibles direcciones ortogonales. Dado que $S$ es una matriz simétrica $n \times n$ siempre existirán $n$ autovectores ortonormales $u_i$ y como la varianza viene dada por los autovalores $\lambda_i$, el procedimiento es:

Obtener la matriz de covarianza $S=\frac{1}{N}(X - \bar{x})^T(X - \bar{x})$ a partir de $X$.
Calcular los autovectores $u_i$ de $S$ en orden de mayor a menor valor de los autovalores $\lambda_i$.
Proyectar $X$ sobre las $K$ componentes principales deseadas

from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target']=iris['target']
df.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

from sklearn.decomposition import PCA
X = df.to_numpy()[:,0:4]
y = df.to_numpy()[:,4]
pca = PCA(n_components=None)
X_pca = pca.fit_transform(X)
Varianzas=pca.explained_variance_ratio_
Varianzas

array([0.92461872, 0.05306648, 0.01710261, 0.00521218])

var_exp = pca.explained_variance_ratio_
tot = len(var_exp)
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1,tot+1), var_exp, alpha=0.5, align='center',label='Varianza explicada inidividual')
plt.step(range(1,tot+1), cum_var_exp, where='mid',label='Varianza explicada acumulada')
plt.ylabel('Ratio de varianza explicada')
plt.xlabel('Indice de Característica Principal')
plt.legend(loc='best')
plt.show()

Se eligen 2 componentes y se proyecta y se representa sobre esas 2 componentes

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y), colors, markers):
    plt.scatter(X_pca[y==l, 0], X_pca[y==l, 1], c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower right')
plt.show()

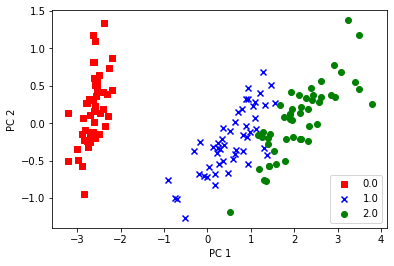
Se revisan los resultados haciendo los cálculos paso a paso

## Calculo de la matriz de covarianza
## means = [ np.mean(X[:,i]) for i in range(X.shape[1])] ## Vector de medias
## S = np.dot(np.transpose(X-means), X-means)/X.shape[0] ## Matriz de covarianza
S = np.cov(X.T)  ## Función de Numpy
## Calculo de los autovalores y autovectores
eigen_vals, eigen_vecs = np.linalg.eig(S)
eigen_vals

array([4.22824171, 0.24267075, 0.0782095 , 0.02383509])

var_exp = eigen_vals / np.sum(eigen_vals)  ## Calculamos en ratio
tot = len(var_exp)
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1,tot+1), var_exp, alpha=0.5, align='center',label='Varianza explicada inidividual')
plt.step(range(1,tot+1), cum_var_exp, where='mid',label='Varianza explicada acumulada')
plt.ylabel('Ratio de varianza explicada')
plt.xlabel('Indice de Característica Principal')
plt.legend(loc='best')
plt.show()

El método de componentes principales no está dirigido a seleccionar las características de la matriz inicial X con más varianza, sino que permiten proyectar sobre un nuevo espacio K-dimensional eligiendo las dimensiones que garantizan un ratio de la varianza total.

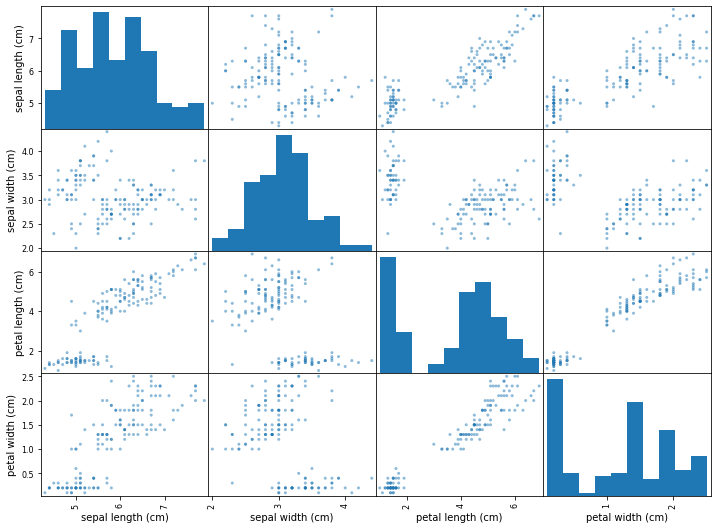
Matriz de correlación y gráfico de dispersión entre características¶

Aunque está más dirigido a los problemas de regresión entre variables continuas, es posible hacer un estudio de que caracteristicas se correlacionan mejor entre sí o bien a traves de la matriz de correlación o dibujando el gráfico de dispersión 2 a 2 de todas las características de X

Por ejemplo en el conjunto Iris la matriz de correlación entre las 4 características de la matriz X y el grafico de dispersión entre las características es:

df_cov = pd.DataFrame(np.corrcoef(X.T), columns=iris.feature_names)
df_cov.insert(loc=0, column='Correlación', value=iris.feature_names)
df_cov

	Correlación	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	sepal length (cm)	1.000000	-0.117570	0.871754	0.817941
1	sepal width (cm)	-0.117570	1.000000	-0.428440	-0.366126
2	petal length (cm)	0.871754	-0.428440	1.000000	0.962865
3	petal width (cm)	0.817941	-0.366126	0.962865	1.000000

Gráfico de dispersión entre características

axes=pd.plotting.scatter_matrix(df[iris.feature_names], figsize=(12,9))

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

Introducción al Aprendizaje Automático