Contents

03.3 Clustering. Análisis de microarrays

Objetivos de la práctica

  • Utilizar datos de microarrays para agrupar genes en función de sus patrones de expresión.

  • Comparar los grupos obtenidos con los diferentes tipos de cáncer anotados.

El conjunto de datos NCI60 contiene información genética de 64 líneas celulares cancerígenas. Para cada una de ellas, se ha cuantificado la expresión de 6830 genes mediante tecnología microarray. Se conoce el tipo de cáncer (histopatología) al que pertenece cada línea celular y se puede utilizar esta información para evaluar si el método de clustering (agglomerative hierarchical clustering) es capaz de agrupar correctamente las líneas empleando los niveles de expresión génica.

import matplotlib.pyplot as plt 
%matplotlib inline
import pandas as pd
import numpy as np
from skimage import io
from IPython import display

Carga de Datos

Descargar el archivo que se encuentra en Moodle con el nombre nci_data.csv y situarlo en una carpeta de nombre data en el path donde se encuentre el cuaderno Jupyter.

df = pd.read_csv('data/nci_data.csv')
df.head()
Gene s1 s2 s3 s4 s5 s6 s7 s8 s9 ... s55 s56 s57 s58 s59 s60 s61 s62 s63 s64
0 g1 0.300 0.679961 0.940 0.280 0.485 0.310 -0.830 -0.190 0.460 ... 0.010 -0.620 -0.380 0.04998 0.650 -0.030 -0.270 0.210 -0.050 0.350
1 g2 1.180 1.289961 -0.040 -0.310 -0.465 -0.030 0.000 -0.870 0.000 ... -1.280 -0.130 0.000 -0.72002 0.640 -0.480 0.630 -0.620 0.140 -0.270
2 g3 0.550 0.169961 -0.170 0.680 0.395 -0.100 0.130 -0.450 1.150 ... -0.770 0.200 -0.060 0.41998 0.150 0.070 -0.100 -0.150 -0.090 0.020
3 g4 1.140 0.379961 -0.040 -0.810 0.905 -0.460 -1.630 0.080 -1.400 ... 0.940 -1.410 0.800 0.92998 -1.970 -0.700 1.100 -1.330 -1.260 -1.230
4 g5 -0.265 0.464961 -0.605 0.625 0.200 -0.205 0.075 0.005 -0.005 ... -0.015 1.585 -0.115 -0.09502 -0.065 -0.195 1.045 0.045 0.045 -0.715

5 rows × 65 columns

Los 64 tipos de cancer se encuentra en el archivo nci_label.txt también situado en Moodle y se descarga a la misma carpeta data

df_lbl = pd.read_csv('data/nci_label.txt', header=None, names=["Cell"])
df_lbl.head()
labels_ok = df_lbl.values
np.size(labels_ok), np.unique(labels_ok)

(64,
 array(['BREAST', 'CNS', 'COLON', 'K562A-repro', 'K562B-repro', 'LEUKEMIA',
        'MCF7A-repro', 'MCF7D-repro', 'MELANOMA', 'NSCLC', 'OVARIAN',
        'PROSTATE', 'RENAL', 'UNKNOWN'], dtype=object))

La estructura del fichero nci_data.csv es:

  • Una columna que sirve para enumerar las 6830 expresiones genéticas y que no se utilizará.

  • 64 columnas con los tipos de cancer.

Por tanto, se toman las 64 últimas columnas, por lo que es necesario transponer la matriz X_trap para obtener el conjunto inicial de entrenamiento, que se denomina X_ini.

X_ini ya tiene 64 filas por cada tipo histológico de cancer con 3680 características, siendo cada uno de ellos la expresión de un gen.

X_trap = df.values[:,1:65]
X_ini = np.transpose(X_trap)
X_ini.shape

(64, 6830)

Estandarización de los datos de entrada

Para poder probar con datos estandarizados o no estandarizados en la siguiente celda tenemos las dos opciones de forma que en la matriz X con la que se va a trabajar se podrá volcar el dato estandarizado o no, según se comente o descomente la última línea de código

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X_ini)
#X = X_ini

Elección del número de clusters

Criterio de Inercia (suma de distancias al cuadrado a los centroides)

Se calcula la inercia relativa a Suma de Distancias al Cuadrado del modelo completo, que se puede calcular con 1 cluster

from sklearn.cluster import KMeans
import sklearn.metrics as metrics
km = KMeans(n_clusters=1, init='k-means++', max_iter=300, tol=1e-04, random_state=1)
km.fit(X)
tss=km.inertia_
distortions = []
for i in range(2, 20):
    km = KMeans(n_clusters=i, init='k-means++', max_iter=300, tol=1e-04)
    km.fit(X)
    distortions.append(km.inertia_/tss)
    
plt.figure(figsize=(7, 4), dpi=80)
plt.plot(range(2,20), distortions, label="SSE rel. vs K")
plt.xlabel("Número de Clusters")
plt.ylabel("Inercia relativa")
plt.legend(loc='upper right')
plt.show()
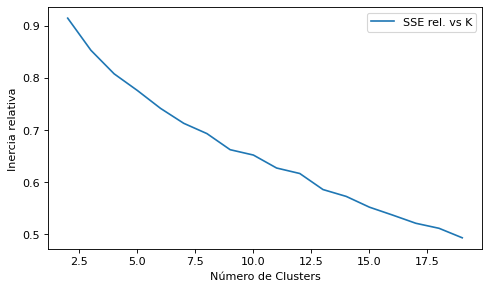
_images/03.3_Clustering_Analisis_Microarrays_12_0.png

Conclusión del gráfico del codo: no resulta muy concluyente por el escaso número de registros de la matriz X, por lo que se echa mano de otro criterio de validación intrínseca que es el criterio de la Silueta

Criterio de la Silueta

El coeficiente de silueta se calcula utilizando la distancia media dentro del grupo (a) y la distancia media del grupo más cercano (b) para cada muestra. El Coeficiente de silueta para una muestra es (b - a) / max(a, b). Para aclarar, b es la distancia entre una muestra y el grupo más cercano del que la muestra no forma parte. El coeficiente de silueta solo se define si el número de etiquetas es \(2 \ge N_{labels} \ge N_{samples} - 1\)

El mejor valor es 1 y el peor valor es -1. Los valores cercanos a 0 indican clústeres superpuestos. Los valores negativos generalmente indican que una muestra se ha asignado al conglomerado equivocado, ya que un conglomerado diferente es más similar.

from sklearn.cluster import KMeans
import sklearn.metrics as metrics
siluetas = []
for i in range(2, 20):
    km = KMeans(n_clusters=i, init='k-means++', max_iter=300, tol=1e-04, random_state=1)
    km.fit(X)
    silueta = metrics.silhouette_score(X,km.labels_,metric="euclidean",sample_size=1000)
    #print(i, km.inertia_, tss, km.inertia_/tss)
    siluetas.append(silueta)

plt.figure(figsize=(7, 4), dpi=80)
plt.plot(range(2,20), siluetas, label="Silueta vs K")
plt.xlabel("Número de Clusters")
plt.ylabel("Silueta")
plt.legend(loc='upper right')
plt.show()
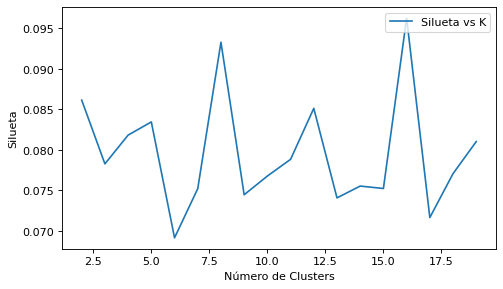
_images/03.3_Clustering_Analisis_Microarrays_15_0.png

Conclusión del gráfico de la Silueta: Los mejores valores están primero en 8 y luego en 16 grupos.

Vamos a crear una variable con el número de grupos para poder cambiar dicho valor sin tocar el resto de código

Como se sabe que hay 14 tipos de cancer, este debería ser el valor teórico que nos debería haber salido si el clustering ajustara perfectamente la realidad

print("Total tipos de cancer", np.size(np.unique(labels_ok)))
totalClusters = 14

Total tipos de cancer 14

Cluster Jerarquico

Se calcula con el número de clusters indicado anteriormente

from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=totalClusters, affinity='euclidean', linkage='complete', compute_distances=True)
#ac = AgglomerativeClustering(n_clusters=14, affinity='euclidean', linkage='complete', distance_threshold=None)
y_ag = ac.fit_predict(X)
y_ag, ac.distances_[-1], 0.7*ac.distances_[-1], ac.n_clusters_

(array([ 2,  2,  2,  9,  1,  1,  1,  1,  0,  2,  2,  2,  2,  2,  6,  6,  6,
         4,  4,  8,  6,  6,  0,  0,  0,  0,  0,  6,  0,  0,  2,  0,  0,  3,
         3,  3,  3,  3, 13, 13, 12,  0, 10,  0, 10, 10, 10, 10,  5,  5,  5,
         5,  0,  0, 11,  7,  7,  7,  9,  7,  7,  7,  7,  7]),
 163.48974041519423,
 114.44281829063596,
 14)

Se echa un primer vistazo al aspecto que tiene la agrupación conseguida

etiquetas=np.unique(y_ag) 
numEtiquetas = np.size(etiquetas)
maxSizeCluster=0
for et in etiquetas:
    print(et, np.size(y_ag[y_ag==et]), y_ag[y_ag==et])

0 14 [0 0 0 0 0 0 0 0 0 0 0 0 0 0]
1 4 [1 1 1 1]
2 9 [2 2 2 2 2 2 2 2 2]
3 5 [3 3 3 3 3]
4 2 [4 4]
5 4 [5 5 5 5]
6 6 [6 6 6 6 6 6]
7 8 [7 7 7 7 7 7 7 7]
8 1 [8]
9 2 [9 9]
10 5 [10 10 10 10 10]
11 1 [11]
12 1 [12]
13 2 [13 13]

Se lista con mayor detalle los grupos obtenidos y los tipos de cancer asignados a cada uno de ellos con su nombre

pd.set_option('display.width', 1000)
tiposCancerGrupo = ['' for i in range(numEtiquetas)]
for iCancer in range(np.size(y_ag)):
    iCluster = y_ag[iCancer]
    tiposCancerGrupo[iCluster] += str(labels_ok[iCancer]) + ";"

for i in range(np.size(tiposCancerGrupo)):
    print(i, tiposCancerGrupo[i])

0 ['NSCLC'];['MELANOMA'];['PROSTATE'];['OVARIAN'];['OVARIAN'];['OVARIAN'];['OVARIAN'];['PROSTATE'];['NSCLC'];['NSCLC'];['COLON'];['COLON'];['NSCLC'];['NSCLC'];
1 ['BREAST'];['CNS'];['CNS'];['BREAST'];
2 ['CNS'];['CNS'];['CNS'];['NSCLC'];['RENAL'];['RENAL'];['RENAL'];['RENAL'];['NSCLC'];
3 ['LEUKEMIA'];['K562B-repro'];['K562A-repro'];['LEUKEMIA'];['LEUKEMIA'];
4 ['BREAST'];['NSCLC'];
5 ['MCF7A-repro'];['BREAST'];['MCF7D-repro'];['BREAST'];
6 ['RENAL'];['RENAL'];['RENAL'];['UNKNOWN'];['OVARIAN'];['OVARIAN'];
7 ['MELANOMA'];['BREAST'];['BREAST'];['MELANOMA'];['MELANOMA'];['MELANOMA'];['MELANOMA'];['MELANOMA'];
8 ['RENAL'];
9 ['RENAL'];['MELANOMA'];
10 ['COLON'];['COLON'];['COLON'];['COLON'];['COLON'];
11 ['NSCLC'];
12 ['LEUKEMIA'];
13 ['LEUKEMIA'];['LEUKEMIA'];

Función a la medida para graficar el Dendograma

Disponible en el “03.0ClusteringUtilidades.ipynb”

run 03.0_ClusteringUtilidades.ipynb

load done!

titulo="Análisis de Microarrays"
subtitulo="Tipos de Cáncer"
figSize=(15,10)
plot_dendrogram(ac, titulo, subtitulo, figSize, leaf_font_size=10)
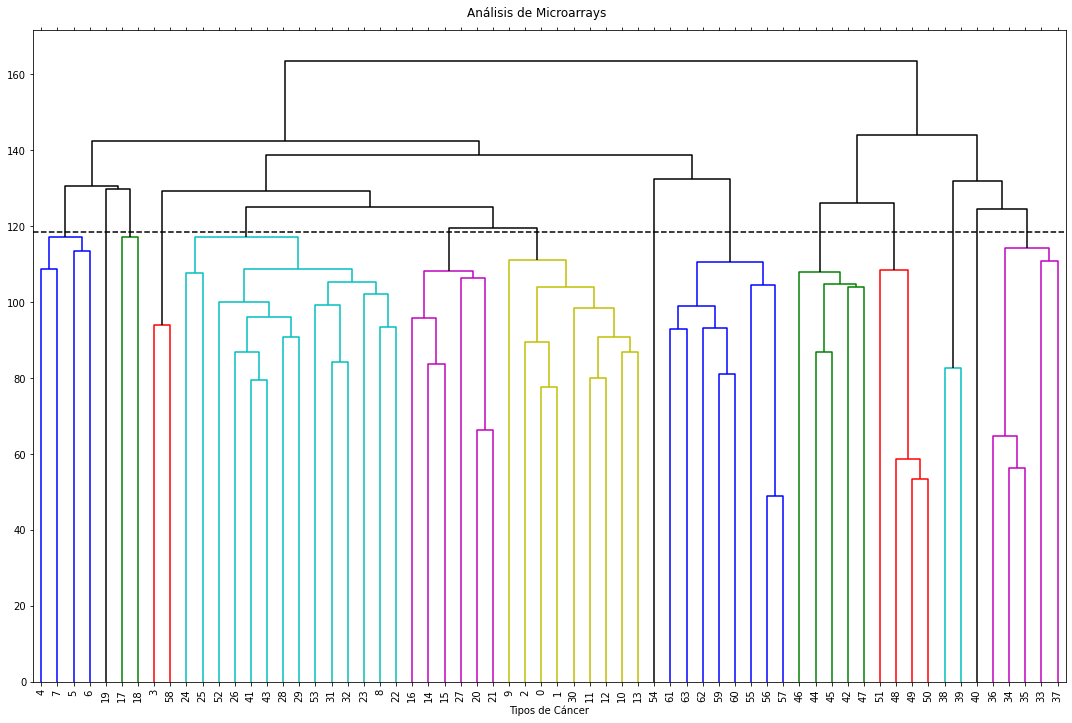
_images/03.3_Clustering_Analisis_Microarrays_26_0.png

Se valida el cluster jerárquico

ac = AgglomerativeClustering(n_clusters=14, affinity='euclidean', linkage='complete')
y_ag = ac.fit_predict(X)

from sklearn.metrics.cluster import rand_score
from sklearn.metrics.cluster import adjusted_rand_score
y_ok = [lbl[0] for lbl in labels_ok]
## Rand - Puntuación de similitud entre 0.0 y 1.0, (1.0 significa coincidencia perfecta)
R=rand_score(labels_true=y_ok, labels_pred=y_ag) 
ARI=adjusted_rand_score(labels_true=y_ok, labels_pred=y_ag)
R, ARI, y_ok

(0.8720238095238095,
 0.2645020065669464,
 ['CNS',
  'CNS',
  'CNS',
  'RENAL',
  'BREAST',
  'CNS',
  'CNS',
  'BREAST',
  'NSCLC',
  'NSCLC',
  'RENAL',
  'RENAL',
  'RENAL',
  'RENAL',
  'RENAL',
  'RENAL',
  'RENAL',
  'BREAST',
  'NSCLC',
  'RENAL',
  'UNKNOWN',
  'OVARIAN',
  'MELANOMA',
  'PROSTATE',
  'OVARIAN',
  'OVARIAN',
  'OVARIAN',
  'OVARIAN',
  'OVARIAN',
  'PROSTATE',
  'NSCLC',
  'NSCLC',
  'NSCLC',
  'LEUKEMIA',
  'K562B-repro',
  'K562A-repro',
  'LEUKEMIA',
  'LEUKEMIA',
  'LEUKEMIA',
  'LEUKEMIA',
  'LEUKEMIA',
  'COLON',
  'COLON',
  'COLON',
  'COLON',
  'COLON',
  'COLON',
  'COLON',
  'MCF7A-repro',
  'BREAST',
  'MCF7D-repro',
  'BREAST',
  'NSCLC',
  'NSCLC',
  'NSCLC',
  'MELANOMA',
  'BREAST',
  'BREAST',
  'MELANOMA',
  'MELANOMA',
  'MELANOMA',
  'MELANOMA',
  'MELANOMA',
  'MELANOMA'])

Acceso a las rutinas de cálculo de la Variación de Información de Meilă

from sklearn.metrics.cluster import mutual_info_score
from sklearn.metrics.cluster import adjusted_mutual_info_score
VI = variationInformation(y_ok, y_ag)
## El VI devuelve un valor de 0 cuando las dos particiones son idénticas (es decir, coinciden perfectamente)
## El VI ajustado es un valor independiente del número de registros N
adj_VI = adjustedVariationInformation(y_ok, y_ag)
VI, adj_VI

(0.244285988549783, 0.05873836403990501)

Representación desde PCA

from sklearn.decomposition import PCA
pca = PCA(n_components=None)
X_pca = pca.fit_transform(X)
Varianzas=pca.explained_variance_ratio_

var_exp = pca.explained_variance_ratio_
tot = len(var_exp)
cum_var_exp = np.cumsum(var_exp)
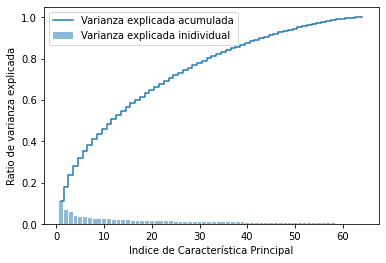
import matplotlib.pyplot as plt
plt.bar(range(1,tot+1), var_exp, alpha=0.5, align='center',label='Varianza explicada inidividual')
plt.step(range(1,tot+1), cum_var_exp, where='mid',label='Varianza explicada acumulada')
plt.ylabel('Ratio de varianza explicada')
plt.xlabel('Indice de Característica Principal')
plt.legend(loc='best')
plt.show()
_images/03.3_Clustering_Analisis_Microarrays_34_0.png 
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)

lstEtiquetas = np.squeeze(labels_ok, axis=1)
etiquetas=np.unique(lstEtiquetas)
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'brown', 'navy', 'coral', 'lime', 'orange', 'violet', 'wheat']
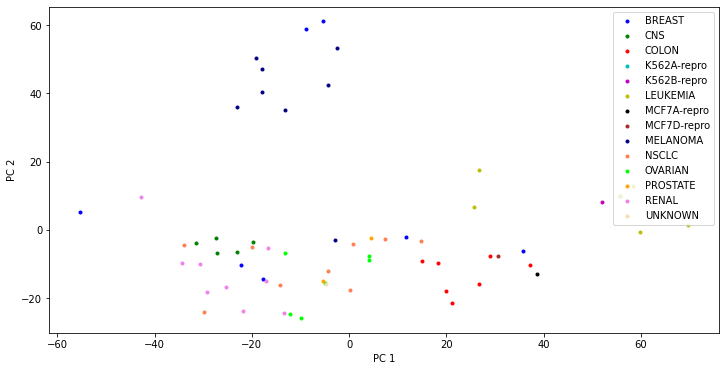
plt.figure(figsize=(12, 6))
for l, c in zip(etiquetas, colors):
    plt.scatter(X_pca[lstEtiquetas==l, 0], X_pca[lstEtiquetas==l, 1], c=c, label=l, marker='.')

plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='upper right')
plt.show()
_images/03.3_Clustering_Analisis_Microarrays_36_0.png 
lstEtiquetas = np.squeeze(labels_ok, axis=1)
etiquetas=np.unique(lstEtiquetas)
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'brown', 'navy', 'coral', 'lime', 'orange', 'violet', 'wheat']
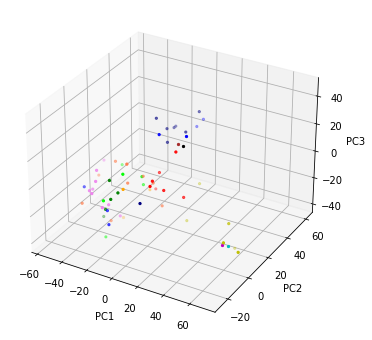
fig=plt.figure(figsize=(12, 6))
ax = fig.add_subplot(projection='3d')
for l, color in zip(etiquetas, colors):
    #ax.scatter(X_pca[lstEtiquetas==l, 0], X_pca[lstEtiquetas==l, 1], X_pca[lstEtiquetas==l, 2], c=c, label=l, marker='.')
    ax.scatter(X_pca[lstEtiquetas==l, 0], X_pca[lstEtiquetas==l, 1], X_pca[lstEtiquetas==l, 2], c=color, label=l, marker='.')


ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')

#plt.legend(loc='upper left')
plt.show()
_images/03.3_Clustering_Analisis_Microarrays_37_0.png

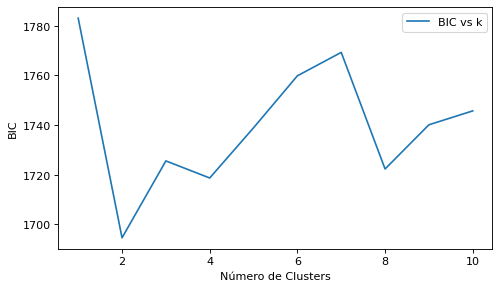
Método del Codo sobre las 3 componentes principales

from sklearn.mixture import GaussianMixture
bic = []
for i in range(1, 11):
    gmm = GaussianMixture(n_components=i, init_params='kmeans')
    gmm.fit(X_pca)
    bic.append(gmm.bic(X_pca))

plt.figure(figsize=(7, 4), dpi=80)
plt.plot(range(1,11), bic, label="BIC vs k")
plt.xlabel("Número de Clusters")
plt.ylabel("BIC")
plt.legend(loc='upper right')
plt.show()
_images/03.3_Clustering_Analisis_Microarrays_39_0.png

previous

03.2 Otros métodos de agrupación - Clustering Jerárquico y Densidad

next

03.4 Ejercicio de Clustering con fichero de semillas