Formulación genérica

En la sección 2.1 se hizo hincapié en el punto de vista de Lagrange. Este punto de vista es el natural para formular un método de partículas lagrangianas, igual que la imagen de Euler es la natural para los métodos de malla fija.

Una partícula en nuestra simulación será, por tanto, un pequeño sistema físico con sus magnitudes correspondientes. Para una partícula $a$ , de una total de $N$ , tendremos: la masa $M_a$ , volumen $\mathcal{V}_a$ , velocidad $v_a$ , energía interna $e_a$ ...

Una aplicación directa de las ecuaciones (2.1) y (2.2) nos proporciona estas ecuaciones de movimiento de una partícula lagrangiana:

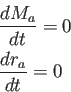$$\begin{split}& \frac{dM_a}{dt}=0\\ & \frac{dr_a}{dt}=0\\ \end{split}$$ (4.3)

El cambio en velocidad vendrá dado por la ecuación de Navier-Stokes (2.8), ``particularizada'':

$$\rho_a \frac{d v_a}{d t}= \rho_a g - \nabla_a p + \nabla_a \cdot (\mu_a \overline{\nabla_a v}+ \lambda_a (\nabla_a \cdot v) \bar{1} ).$$ (4.4)

En esta ecuación todos los términos son bastante fáciles de evaluar salvo los operadores diferenciales espaciales. En efecto, con $\nabla_a$ nos referimos en ella a ``una aproximación para el operador $\nabla$ en la partícula $a$ ''. La dificultad radica justamente en cómo definir un operador que tenga propiedades numéricas adecuadas.