El gradiente

Para obtener una expresión para el gradiente, consideremos la ecuación de Euler para una partícula,

$$\rho_a \frac{d v_a}{d t}= - \nabla_a p ,$$ (4.8)

donde omitimos el término gravitacional, que no conlleva ninguna dificultad.

En la sección anterior conectamos una ecuación tomada del continuo con otra procedente de la regla de la cadena y de la condición del volumen de una partícula. Ahora seguiremos el mismo camino, definiendo la energía de una partícula $a$ como en (2.10):

$$E_a= U_a +\frac{1}{2} m_a v_a^2 .$$ (4.9)

La energía total del sistema es

$$E=\sum_a E_a = \sum_a \left( U_a +\frac{1}{2} m_a v_a^2 \right).$$

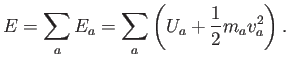
Igual que en el caso continuo, (2.11), el cambio de la energia sera

$$\frac{dE}{dt}= \sum_a \left( m_a v_a \cdot \frac{dv_a}{dt} + \frac{d U_a}{d\mathcal{V}_a} \frac{d\mathcal{V}_a}{dt} \right).$$ (4.10)

Por otro lado, conocemos la relación termodinámica

$$-p=\frac{\partial U}{\partial V} ,$$

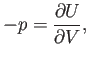
válida para un proceso adiabático. Así pues,

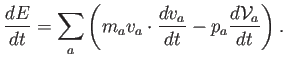$$\frac{dE}{dt}= \sum_a \left( m_a v_a \cdot \frac{dv_a}{dt}- p_a \frac{d\mathcal{V}_a}{dt} \right).$$ (4.11)

Introduciendo la ecuación (4.6),

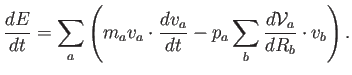$$\frac{dE}{dt}= \sum_a \left( m_a v_a \cdot \frac{dv_a}{dt}- p_a \sum_b \frac{d \mathcal{V}_a}{dR_b} \cdot v_b \right).$$ (4.12)

Para recuperar la ecuación de Euler, este cambio de energía debe ser nulo:

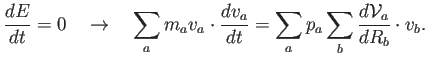$$\frac{dE}{dt}= 0 \quad \rightarrow \quad \sum_a m_a v_a \cdot \frac{dv_a}{dt} = \sum_a p_a \sum_b \frac{d \mathcal{V}_a}{dR_b} \cdot v_b .$$ (4.13)

Vemos que una posibilidad de satisfacer esta ecuación es definiendo

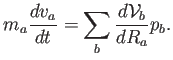$$m_a \frac{dv_a}{dt} = \sum_b \frac{d \mathcal{V}_b}{dR_a} p_b .$$ (4.14)

Una comparación con la ecuación de Euler (4.8) revela que acabamos de introducir una aproximación para el gradiente de la presión:

$$\nabla_a p \doteq -\frac{1}{\mathcal{V}_a} \sum_b \frac{d \mathcal{V}_b}{dR_a} p_b .$$ (4.15)

Esta es una expresión similar a la de la divergencia (4.7), pero con sutiles diferencias: un cambio de signo y una inversión de $a$ y $b$ en la derivada. Además, estos dos operadores son mutuamente adjuntos en cierto sentido, como se discute en [14].