Elementos finitos en 1D

En una dimensión es muy sencillo evaluar las integrales que aparecen en la matriz de rigidez y de masas. El resultado final para el laplaciano (en la aproximación de masa acumulada) es:

$$(\nabla^2 f)_a \doteq \frac{2}{h_{a-}+h_{a+}} \left[ \frac{f_{a+... ..._{a-}} - \left( \frac{1}{h_{a-}} + \frac{1}{h_{a+}} \right) f_a , \right]$$

donde $h_{a-}$ es el intervalo entre la posición del nodo $a$ y el de su izquierda, $h_{a-}=x_a-x_{a-1}$ y $h_{a+}=x_{a+1}-x_a$ el de la derecha.

Esta expresión es, de hecho, la habitual en diferencias finitas (ver sección 4.1.1). Si los intervalos son todos iguales a $h$ , la expresión es muy conocida:

$$(\nabla^2 f)_a \doteq \frac{1}{h^2} \left[ f_{a+1} +f_{a-1} -2 f_a . \right]$$

Las propiedades de esta aproximación son excelentes: verifica consistencia de orden cero, $\nabla^2 c \doteq 0$ , consistencia de primer orden, $\nabla^2 x \doteq 0$ y consistencia de segundo orden, $\nabla^2 x^2 \doteq 2$ , para cualquier conjunto de nodos. Lo último es sorprendente: las funciones base tienen segundas derivadas patológicas; sin embargo, las primeras derivadas, dentro de un método de Galerkin, proporcionan la segunda derivada exacta.

Para completar la discusión, los elementos de la matriz de masas son

$$m_{a,a}=\frac{1}{3}(h_{a-}+h_{a+})$$

$$m_{a,a-1}=\frac{1}{6} h_{a-}$$

$$m_{a,a+1}=\frac{1}{6} h_{a+}$$

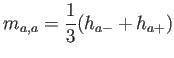
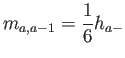
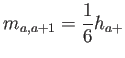
Puede comprobarse que se recupera la expresión para la masa acumulada, $m_a= m_{a,a}+m_{a,a-1}+m_{a,a+1}$ .

A la hora de implementar estas expresiones (que son lo bastante sencillas para requerir un pequeño programa en un programa de cálculo estilo matlab, u octave) es interesante que las matriz de rigidez es, en un enfoque ingenuo, singular. Por ejemplo, para $4$ nodos equiespaciados (ponemos $h=1$ por claridad):

$$\Lambda= \left( \begin{array}{cccc} -1 & 1 & 0 & 0 \\ 1 & ... ... 0 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & -1 \end{array}\right);$$

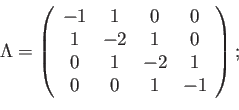
una matriz claramente singular (basta sumar filas sucesivamente). El álgebra lineal nos está indicando, a su manera, que el problema está mal condicionado porque falta una parte importante: las condiciones en la frontera. Por ejemplo, si estas son de Dirichlet homogéneas en los dos extremos, estas condiciones se reflejan en la matriz de rigidez, que pasa a ser:

$$\Lambda= \left( \begin{array}{cccc} -2 & 1 & 0 & 0 \\ 1 & -2 & 1 & 0 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & -2 \end{array} \right) ,$$ (4.1)

la cual ya no es singular. En general, la idea es introducir ``a mano'' las condiciones en la frontera en las matrices de rigidez y de masas. Para esto último puede ser útil introducir nodos de frontera que luego no aparecen en las matrices. En la matriz anterior, habría entonces un ``nodo 0 '', a la izquierda del primero, y otro ``$N+1$ '' a la derecha del último.

Otra opción es añadir explícitamente estos dos nodos de frontera a la matriz, escribiendo dos filas adicionales bastante triviales:

$$\Lambda= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 &0 \\ -1&-2 & 1 & 0 &... ...& -2 & 1 &0 \\ 0& 0 & 0 & 1 & -2 &1 \\ 0 & 0 & 0 & 0 & 0 &1 \end{pmatrix} .$$

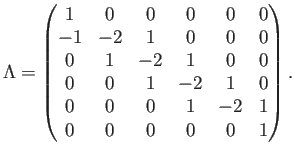
La matriz de masas deberá tener dos filas análogas; por último, el vector $g$ debe contener dos elementos adicionales, correspondientes al valor de la función $f$ en los dos extremos del dominio (para el caso homogéneo sería ambos cero, pero pueden usarse otros valores). De este modo forzamos a que la función $f$ satisfaga los valores deseados en los extremos, mientras la conexión con los nodos internos está garantizada por la parte original de las matrices. Un inconveniente es que las matrices ya no son simétricas.

La última opción es quizá más elegante: consiste en alterar la parte derecha de la ecuación de Poisson para incluir las condiciones de contorno adecuadas, partiendo de las de Dirichlet homogéneas (4.1), ver [11], p. 377.