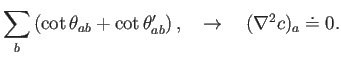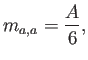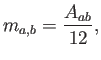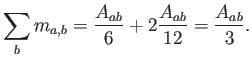Las integrales son más complicadas en dos dimensiones, pero son bastante
asumibles, dado que los elementos son lineales a trozos. Es evidente que un
nodo sólo tiene solapamiento con sus vecinos de Voronoi (o Delaunay). Así
pues, las integrales son sobre triángulos. El resultado final es:
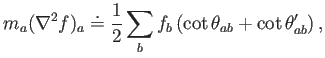 |
(4.2) |
donde 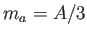 , un tercio del área de la base del elemento (la suma
de las áreas de los triángulos incidentes) y los dos ángulos son los
dos ángulos externos compartidos por el nodo
, un tercio del área de la base del elemento (la suma
de las áreas de los triángulos incidentes) y los dos ángulos son los
dos ángulos externos compartidos por el nodo 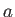 y su vecino
y su vecino 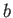 (ver
figura 4.2). Esta es la conocida ``fórmula de la
cotangente''. Como esta función trigonométrica tiende a 0
cuando los
ángulos tienen al recto, esto significa que el papel de un nodo
(ver
figura 4.2). Esta es la conocida ``fórmula de la
cotangente''. Como esta función trigonométrica tiende a 0
cuando los
ángulos tienen al recto, esto significa que el papel de un nodo 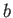 es
menor cuando sus triángulos son abiertos en la dirección que une
es
menor cuando sus triángulos son abiertos en la dirección que une 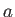 y
y
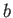 . En cambio, cuando son cerrados o abiertos su papel es muy grande,
al tender la contangente a infinito cuando su argumento tiende a cero
o a dos ángulos rectos. Vemos que esta expresión del laplaciano
incorpora por tanto una noción de la distorsión de una triangulación.
. En cambio, cuando son cerrados o abiertos su papel es muy grande,
al tender la contangente a infinito cuando su argumento tiende a cero
o a dos ángulos rectos. Vemos que esta expresión del laplaciano
incorpora por tanto una noción de la distorsión de una triangulación.
Cuando 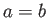 , la fórmula es la que satisface consistencia de orden cero:
, la fórmula es la que satisface consistencia de orden cero:
En la práctica, es más útil utilizar este hecho que evaluar la expresión
completa.
Figura:
Los dos ángulos de la
fórmula de la cotangente.
|
|
Como este método es ampliamente utilizado, han aparecido numerosos trabajos
sobre las propiedades de esta aproximación [12,13].
En cuanto a la matriz de masas, los elementos son
con la misma área 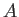 que aparecía en
que aparecía en 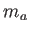 , y
, y
donde 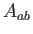 es el área de los dos triángulos compartidos
por
es el área de los dos triángulos compartidos
por 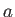 y
y 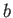 . Sumando para cada triángulo, dado que existen
dos nodos distintos de
. Sumando para cada triángulo, dado que existen
dos nodos distintos de 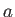 , se tendrá
, se tendrá
Sumando a todos los triángulos incidentes a 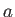 se recupera la expresión para la masa acumulada,
se recupera la expresión para la masa acumulada,
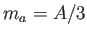 .
Daniel Duque
2011-11-10
.
Daniel Duque
2011-11-10
![]() , la fórmula es la que satisface consistencia de orden cero:
, la fórmula es la que satisface consistencia de orden cero: