Escalado y similitud

Como las ecuaciones de la hidrodinámica son bastante complicadas, es conveniente, como en otros muchos ámbitos, definir variables sin dimensiones físicas. Esto conlleva una serie de ventajas:

• Simplicidad en las ecuaciones, al tener que acarrear menos parámetros.
• Generalidad en los resultados, que se aplican ahora a multitud de situaciones físicas.
• Identificación de los parámetros relevantes.

El método más habitual es identificar en un problema estos parámetros relevantes:

Longitud $L$

La longitud característica del problema. Por ejemplo: el radio de un cilindro inmerso en un fluido, el radio de una tubería, la eslora de un barco.

Propiedades del flujo libre

Estas son las magnitudes físicas que corresponderían a un problema simplificado. En particular, nos interesan la densidad del flujo libre, $\rho_0$ , su presión $p_0$ y ...

Velocidad $v_0$

Una velocidad de referencia, por lo general correspondiente al flujo libre, puntos lejanos o fronteras móviles: velocidad de un fluido lejos de un obstáculo, velocidad de crucero de un barco...En un problema de convección, puede tomarse la velocidad típica de convección, $v_0=\mu_0/(\rho_0 L)$ .

En términos de estas variables, se pueden definir magnitudes sin dimensiones:

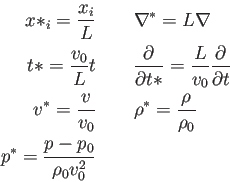$$\begin{split}x*_i=\frac{x_i}{L} & \qquad \nabla^*=L\nabla \\ ... ...rho}{\rho_0} \\ p^*=\frac{p-p_0}{\rho_0 v_0^2} & \\ \end{split}$$ (2.12)

Es interesante ver qué sucede con las ecuaciones de la hidrodinámica al usar estas magnitudes sin dimensiones. La ecuación de continuidad, (2.5), no cambia en absoluto al pasar a estas magnitudes. Es decir, la continuidad no se ve afectada por los parámetros del fluido.

La ecuación de Navier-Stokes en su forma más sencilla, (2.9), se transforma en otra casi idéntica en variables sin dimensiones, pero esta vez el término viscoso, en vez de un prefactor $\mu$ pasa a tener otro.

$$\mu \rightarrow \frac{\mu}{\rho_0 v_0 L} .$$

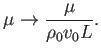
Esta expresión no tiene dimensiones; es tradicional definir más bien su inversa

$$\mathrm{Re}= \frac{\rho_0 v_0 L}{\mu} ,$$

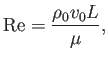
el famoso número de Reynolds^2.4. Por tanto, hemos identificado la combinación de parámetros que determina cómo de viscoso es un flujo. De hecho también se puede escribir

$$\mathrm{Re}= \frac{\rho_0 v_0^2 L^2}{\mu v_0 L} ,$$

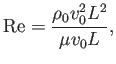
lo cual puede verse como un cociente entre las fuerzas inerciales (de arrastre) y las fuerzas viscosas.

Se pueden considerar estos límites:

$\mathrm{Re}$ pequeña

En este caso, $\mu$ es grande comparada con $\rho_0 v_0 L$ , y el flujo es viscoso. En este caso, dominan los efectos viscosos sobre los inerciales.

$\mathrm{Re}$ grande

En este caso, $\mu$ es pequeña comparada con $\rho_0 v_0 L$ , y el flujo es poco viscoso. En este caso, dominan los efectos inerciales. Sin embargo, se suele argumentar que los efectos viscosos son siempre importantes, aunque estén confinados a una capa límite. Es en este límite cuando puede producirse el fenómeno de la turbulencia.

Otro parámetro que se desprende de la ecuación sin dimensiones es el siguiente:

$$\mathrm{Fr}= \frac{v_0^2}{g L} ,$$

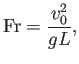
el número de Froude. Este número es importante siempre que la gravedad lo es. En particular, para fenómenos de superficie libre tales como olas y todo tipo de problemas navales, al menos para longitudes típicas superiores al centímetro. A escalas inferiores, la tensión superficial empieza a ser importante (y, finalmente, dominante); el número relevante es entonces el de Weber, $\mathrm{We}$ .

Una descripción exhaustiva de todas la variables hidrodinámicas (algunas de ellas asociadas a condiciones de contorno) y los diversos números adimensionales que aparecen queda fuera de este trabajo, referimos de nuevo a textos canónicos como la Ref. [4].