... ``lagrangiano''2.1
La nomenclatura es históricamente incorrecta, ya que ambos puntos de vista se encuentran en el trabajo pionero de Euler. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... material2.2
También hay que recordar los numerosos otros nombres que se usan para esta expresión: derivada convectiva, advectiva, sustantiva, sustancial, lagrangiana, hidrodinámica, de Stokes, siguiendo el movimiento...También distintos símbolos, como ``$ D/Dt$ ''. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... jacobiana2.3
En castellano podemos distinguir con el género la jacobiana, la matriz con las derivadas, y el jacobiano, su determinante. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Reynolds2.4
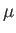En rigor, sería $ \mu_0$ , pero hemos supuesto en esta ecuación simplificada que $ \mu$ es constante. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... nodos3.1
Una triangulación es un ejemplo de una teselación: un recubrimiento del espacio mediante teselas ``iguales''. En este caso, son iguales al ser todas triángulos (tetrahedros en tres dimensiones, símplices en general), aunque por supuesto su forma varía. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 19243.2
La historia de estos conceptos es bastante embrollada. Boris N. Delone, escribía su nombre a la manera francesa, Delaunay, en sus primeros artículos (aunque en realidad su nombre familiar era francés, ``de Launay''). El concepto se remonta en realidad a Voronoı en 1908, quien lo introduzco como dual de su diagrama, aunque fue Delone quien expuso la condición de círculos vacíos. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... importancia3.3
La expresión correcta es diagrama y no teselación, ya que el recubrimiento del espacio es mediante objetos de distinta naturaleza. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...ı3.4
De nuevo, el apellido se escribe ``Voronoi'', ``Voronoı'', o ``Voronoy''. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... bordes3.5
Los bordes (edges) de una triangulación son simplemente los segmentos que conectan los vértices. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... columnas7.1
Las segundas derivadas son tensores de orden tres, que pueden considerarse matrices cuyas columnas son tensores de orden dos ``traducidos'' como hemos explicado anteriormente. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.