Primeras derivadas

La idea es sencilla; por claridad la exponemos para LEM en una dimensión. Igual que para calcular $s_a$ necesitamos conocer el multiplicador $\lambda$ , para calcular $\nabla s_a=s'_a$ necesitamos conocer su derivada $\lambda'$ . Esto se debe a la regla de la cadena:

$$\frac{d s_a}{dx}= \frac{\partial s_a}{\partial x} + \frac{\partial s_a}{\partial \lambda}\frac{\partial \lambda}{\partial x} .$$ (7.2)

Las derivadas parciales de $s_a$ con respecto a $\lambda$ y a $x$ son muy sencillas. Por otro lado, la variación de $\lambda$ está ligada al hecho de que la función objetivo $\log Z$ debe permanecer siempre en un mínimo:

$$\frac{\partial \log Z}{\partial d\lambda} =0 \qquad \mathrm{siempre.}$$

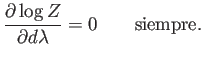
Esto implica

$$\frac{d }{d x} \frac{\partial \log Z}{\partial d\lambda} =0 .$$

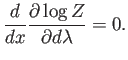
Una nueva aplicación de la regla de la cadena lleva a:

$$\frac{\partial^2 \log Z}{\partial \lambda^2} \lambda ' + \frac{\partial^2 \log Z}{\partial \lambda \partial x} =0 ,$$

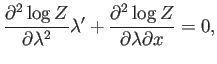
de donde puede despejarse $\lambda'$ , ya que las segundas derivadas de $\log Z$ pueden calcularse de manera bastante sencilla.

La situación en SME es similar, pero como ahora aparece un nuevo multiplicador de Lagrange $\beta$ , obtenemos un sistema de $2$ ecuaciones con $2$ incógnitas: $\lambda'$ y $\beta'$ . Los términos que aparecen son casi todas las derivadas segundas posibles de $\log Z$ respecto a $\lambda$ , $\beta$ y $x$ .

En dimensiones superiores, aparecen subíndices correspondientes a las componentes cartesianas, pero las ecuaciones siguen siendo similares. Este caso, el más general, es el que se muestra en el Apéndice A.1. Es necesario resolver un problema de álgebra lineal, ecuaciones (A.16) y (A.17), o más esquemática, ecuación (A.18). La matriz involucra de nuevo casi todas las posibles derivadas segundas de $\log Z$ , que se indican en las ecuaciones (A.20 - A.26) (sólo falta segunda derivada espacial (A.27)). La solución del sistema proporciona todas las derivadas $d\lambda_{i,j}$ and $d\mu_{st,j}$ . En 2D, estas son $12$ incógnitas: $4$ para las derivadas de $\lambda$ y $8$ para las de $\beta$ (aunque, en realidad, sólo $9$ son independientes gracias a las simetrías). Estas derivadas pueden finalmente combinarse para calcular $\nabla s_a$ , ver ec. (A.12), que no es más que la generalización de (7.2).

Una complejidad añadida a la hora de implementar el método es que los métodos de álgebra lineal se aplican a vectores; nuestras incógnitas son más bien tensores. Por lo tanto, en algún momento (al principio del programa, o justo antes de utilizar las rutinas de álgebra lineal) hace falta ``traducir'' los tensores a vectores, mediante convenios similares al de Voigt. En la práctica, nosotros hemos numerado los ejes cartesianos 0 o $1$ , de tal modo que un elemento de un tensor (sea del orden que sea) vendrá dado por un número en base binaria; por ejemplo, $(1 1)b=3$ . El primer elemento lleva asignado un índice ``0'', pero eso es en todo caso estándar en C y C++.

Este procedimiento aparece en las referencias [31,33], con pequeños cambios de notación (sobre todo con la primera referencia, más antigua).

En resumen, el procedimiento es:

• Minimizar $\log Z$ para calcular $\lambda$ y $\beta$ .
• Calcular las segundas derivadas de $\log Z$ , ecuaciones (A.20 - A.26).
• Utilizarlas para montar la matriz y el vector independiente en el problema de álgebra lineal (A.18).
• Resolver el problema, por ejemplo mediante descomposición LU. Algunas ecuaciones son redundantes, por ejemplo la correspondiente a $\mu_{xy}$ es igual que la de $\mu_{yx}$ . Estas ecuaciones deben ser eliminadas con cuidado, ya que si no muchos algoritmos devuelven un error, al ser la matriz singular. Hemos utilizado el método LU que está implementado en el proyecto de bibliotecas científicas GNU, GSL [34].
• Las derivadas se pueden calcular de (A.14).