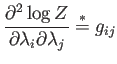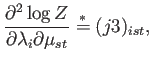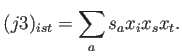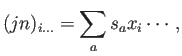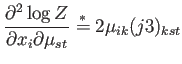Ahora deseamos calcular
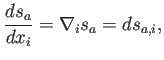 |
(A.11) |
donde la notación ``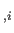 '' significa el componente
'' significa el componente 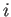 -ésimo de una derivada
espacial (aun así, mantenemos la letra ``
-ésimo de una derivada
espacial (aun así, mantenemos la letra ``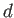 '' for claridad).
'' for claridad).
Por la regla de la cadena,
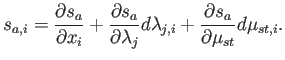 |
(A.12) |
La primera derivada es fácil de obtener:
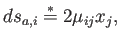 |
(A.13) |
y podemos reducir la Ec. (A.12) a:
![$\displaystyle ds_{a,i} = s_a [ 2\mu_{ij}x_j+ d\lambda_{j,i} x_j+ d\mu_{st,i} (x_s x_t -g_{st}) . ]$](img500.png) |
(A.14) |
Para los otros dos términos, dado que la Ec. (A.8)
debe satisfacerse en todo punto, tenemos
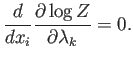 |
(A.15) |
La regla de la cadena entonces lleva a
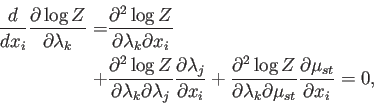 |
(A.16) |
y de la Ec. (A.9),
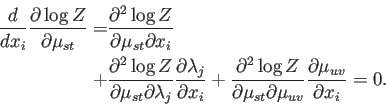 |
(A.17) |
Estas dos ecuaciones tienen la forma de un sistema de ecuaciones
lineales que hay que resolver para
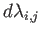 and
and
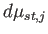 .
En forma matricial esquemática,
.
En forma matricial esquemática,
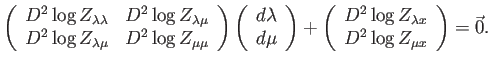 |
(A.18) |
Ahora necesitamos evaluar todas las derivadas de segundo orden de 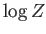 que aparecen en estas expresiones. Para obtenerlas sistemáticamente observamos
que, derivando de nuevo la Ec. (A.7):
que aparecen en estas expresiones. Para obtenerlas sistemáticamente observamos
que, derivando de nuevo la Ec. (A.7):
![$\displaystyle \frac{\partial^2 \log Z}{\partial \xi \partial \phi} = \sum_a s_a...
... f_a}{\partial \xi} + \frac{\partial^2 f_a}{\partial \xi \partial \phi} \right]$](img505.png) |
(A.19) |
Así pues obtenemos las siguientes expresiones.
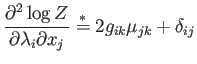 |
(A.20) |
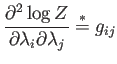 |
(A.21) |
(obsérvese la necesidad de que 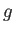 sea simétrico).
sea simétrico).
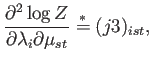 |
(A.22) |
donde 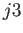 es un tensor de rango
es un tensor de rango 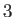 de componentes
de componentes
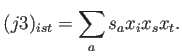 |
(A.23) |
En general, utilizaremos tensores de rango 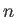
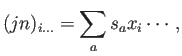 |
(A.24) |
hasta 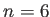 . Nótese que
. Nótese que
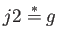 .
.
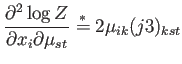 |
(A.25) |
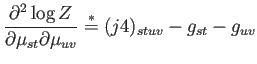 |
(A.26) |
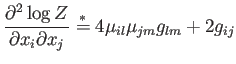 |
(A.27) |
El procedimiento es, por tanto:
- Resolver el problema de la sección anterior.
- Calcular segundas derivadas, Ecs. de (A.20) a
(A.27). (Un cálculo previo de
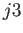 y
y 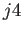 es
recomendable).
es
recomendable).
- Usar estas para construir la matriz y el vector independiente
del problema de álgebra lineal de la Ec. (A.18).
- Resolver el problema lineal. El sistema debe reducirse antes, ya
que algunas ecuaciones son redundantes. Por ejemplo, la ecuación
para
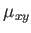 es la misma que para
es la misma que para 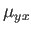 ; esto puede llevar a
errores con algunos códigos numéricos. Hemos empleado la
decompsición LU estándar, según está implementada en las librerías
GSL.
; esto puede llevar a
errores con algunos códigos numéricos. Hemos empleado la
decompsición LU estándar, según está implementada en las librerías
GSL.
- Calcular las derivadas espaciales deseadas mediante la
Ec. (A.14).
Daniel Duque
2011-11-10
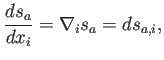
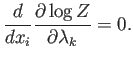
![]() and
and
![]() .
En forma matricial esquemática,
.
En forma matricial esquemática,
![]() que aparecen en estas expresiones. Para obtenerlas sistemáticamente observamos
que, derivando de nuevo la Ec. (A.7):
que aparecen en estas expresiones. Para obtenerlas sistemáticamente observamos
que, derivando de nuevo la Ec. (A.7):