Propiedades de las funciones base

Igual que en el caso sencillo descrito anteriormente, el parámetro libre $\beta$ regula la anchura de las funciones. A la hora de fijar este parámetro, es importante darse cuenta de que lo relevante no es su valor numérico, sino su relación con la distancia entre nodos $h$ . Escribiendo, en una dimensión

$$f_a=\lambda x -\beta x^2 =\lambda h \frac{x}{h} -\beta h^2 \frac{x^2}{h^2} ,$$

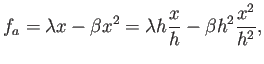
queda claro que lo relevante es $\beta h^2$ en realidad. En cambio, aunque es más elegante tomar $\lambda h$ como valor, este cambio es menos importante porque el valor de $\lambda$ se determina al minimizar la función objetivo. Este hecho no cambia en dimensiones superiores, salvo si se define una $h$ anisotrópica, una posibilidad interesante que hemos explorado, aunque no en profundidad.

En los casos sencillos considerados en [31], $h$ es un escalar constante. A la hora de aplicar este método, en cambio, resulta necesario adecuar $h$ al entorno local de cada nodo, porque si no un valor ``frío'' para puntos espaciados puede resultar ``caliente'' para otros más cercanos.

Una propiedad muy interesante de las funciones base resultantes de LME es su comportamiento en la frontera: a pesar de tener una anchura mucho mayor que la de los elementos finitos, satisfacen la misma condición de frontera que ellos. Esta condición, denominada de ``casi-$\delta$ '' en [31] consiste en que todas las funciones son idénticamente nulas en la frontera del dominio (para ser exactos, en su envolvente convexa); excepto las correspondientes a los nodos que están en la frontera: para estos las funciones alcanzan su máximo. Como se ve en la figura 6.1, las funciones base nunca salen de la envolvente convexa, a pesar de que esta envolvente no se calcula nunca explícitamente.

Figura 6.1: Funciones base LME en dos dimensiones. De [31].

Otra conexión sorprendente con la geometría computacional es el límite muy frío: cuando $\beta \rightarrow \infty$ el término de entropía es despreciable, y puede considerarse la función objetivo

$$F= E + L_0 + L_1.$$

Las funciones base correspondientes al extremo de esta función son, como demostró Rajan [32], los elementos finitos definidos sobre la triangulación de Delaunay. El cálculo de estos elementos suele seguir métodos de geometría computacional, como se ha explicado, pero este método llega a ellos de una manera totalmente distinto. De hecho, el método es algo superior a la triangulación de Delaunay: si existe una configuración degenerada, como la de la figura 6.2, en la que hay cuatro nodos situados en los vértices de un cuadrado, hay dos triangulaciones de Delaunay posibles. En este caso, este método no proporciona ninguna de las dos, sino una función base suavizada, de un orden superior (cuadrático y no lineal).

Figura: Método LME en el límite muy frío para una configuración de nodos cuya triangulación de Delaunay sería degenerada. De [31].