LME

La primera propuesta en aparecer históricamente consiste en una mejora del caso sencillo arriba expuesto para conseguir consistencia a primer orden:

$$\sum_a s_a x_a=x.$$

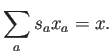
El término de ligadura con el multiplicador de Lagrange necesario es:

$$L_1=\lambda \left(\sum_a s_a (x_a - x) \right) .$$

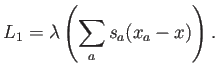
La función objetivo que hay que extremizar es ahora:

$$F= -S +E + L_0 + L_1.$$

Ya no es posible llevar a cabo esta tarea de manera analítica, pero sí se puede hallar el extremo con respecto a los valores $s_a$ , con el siguiente resultado:

$$s_a=\frac{1}{Z}\exp(f_a),$$ (6.1)

donde

$$f_a=\lambda (x-x_a) -\beta (x-x_a)^2$$ (6.2)

y la función de partición es, como antes,

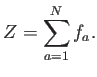$$Z=\sum_{a=1}^N f_a .$$ (6.3)

Al insertar estas expresiones en la función original, el problema queda reducido a encontrar el mínimo de la función $\log Z$ con respecto a $\lambda$ :

$$\min_{\lambda} \log Z .$$ (6.4)

Una vez este mínimo se ha encontrado, los valores en el mímimo de $\lambda$ , que llamaremos $\lambda^*$ , y la función en el mínimo $\log Z^*$ pueden evaluarse para obtener las funciones base según (6.1).