Siguiente: LME Subir: Métodos de máxima entropía Anterior: Métodos de máxima entropía Índice General
La idea principal es que, para lograr la máxima flexibilidad en las funciones base, hay que abandonar la idea que éstas puedan tener una forma determinada prescrita. Por el contrario, deben ser evaluadas punto por punto según ciertos criterios. En general, estas funciones deben ser positivas:
Además, un requisito básico es la consistencia de orden cero, que hace que una función constante se reproduzca exactamente:
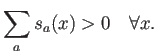
Si ahora aislamos un punto ![]() cualquiera, los valores de las
funciones base son simplemente un conjunto de números
cualquiera, los valores de las
funciones base son simplemente un conjunto de números ![]() . Los
anteriores requisitos son idénticos a los que se requieren de una
serie de probabilidades asociadas a los posibles estados de un
sistema. En este sentido, parece natural tomar ideas de la teoría de
la probabilidad. En particular, la teoría de la información de Shannon
introduce el concepto de entropía de un sistema, inspirado por
la entropía física debida a L. Boltzmann:
. Los
anteriores requisitos son idénticos a los que se requieren de una
serie de probabilidades asociadas a los posibles estados de un
sistema. En este sentido, parece natural tomar ideas de la teoría de
la probabilidad. En particular, la teoría de la información de Shannon
introduce el concepto de entropía de un sistema, inspirado por
la entropía física debida a L. Boltzmann:
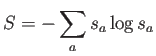
(en lo sucesivo, omitimos la referencia al punto
Esta entropía cumple algunas propiedades atractivas:
Todas estas propiedades son muy conocidas en el área de física estadística, sobre todo cuando los estados son discretos, como en mecánica estadística cuántica. En física se define en realidad
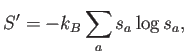
donde la constante de Boltzmann
En general, se suele buscar el extremo de una función objetivo de este tipo:
donde
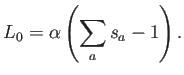
El extremo se alcanza para
Para hacer que el método sea local e incorpore información sobre los nodos, en los métodos de máxima entropía se introduce, como es habitual en física estadística, una energía que debe minimizarse. La forma más típica de esta energía es
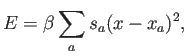
donde
De nuevo, la conexión con la mecánica estadística es clara; en ésta se minimiza la energía libre de Helmholtz
donde
donde
Se puede por tanto considerar el límite
![]() como el
límite ``frío'', que es el dominado por la energía, y
como el
límite ``frío'', que es el dominado por la energía, y
![]() como el ``caliente'', dominado por la entropía.
como el ``caliente'', dominado por la entropía.
El extremo de la función se obtiene facilmente:
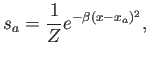
donde
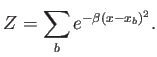
Queda patente que el resultado son funciones base gaussianas, de anchura
Este resultado es, de hecho, idéntico al método SPH con funciones
núcleo (``kernel'') gaussianas, corregidas a la manera de Shepard (a
través del término ![]() ) para satisfacer consistencia de orden cero.
Es trivial recuperar cualquier función nucleo SPH que se desee
cambiando la definición de la energía.
) para satisfacer consistencia de orden cero.
Es trivial recuperar cualquier función nucleo SPH que se desee
cambiando la definición de la energía.