Siguiente: Conservación de la masa Subir: Resumen de hidrodinámica Anterior: Puntos de vista de Índice General
No nos referimos aquí a la cinemática de una partícula puntual, tan conocida. Más bien, a la acción de un campo de velocidades sobre una de nuestras partículas fluidas. Nos limitamos aquí a proporcionar una lista de expresiones relevantes, refiriendo al lector a la excelente descripción de la Ref. [4], p. 19.
Una partícula puede distorsionarse de cuatro maneras distintas bajo un campo de velocidades. Cada una de ellas tiene una tasa, o ritmo, de deformación (strain rate) asociada.
Traslación
Es fácil ver que la tasa de traslación es, casi por definición, la
propia velocidad ![]() .
.
Rotación
La tasa de rotación viene dada por la velocidad angular
![]() .
Debido a un molesto factor
.
Debido a un molesto factor ![]() , se suele definir un vector que es el
doble de la velocidad angular
, se suele definir un vector que es el
doble de la velocidad angular
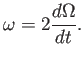
Esta magnitud, de gran importancia, se denomina vorticidad. Su expresión es particularmente sencilla:
es decir, es el rotacional del campo de velocidades.
Por ejemplo,
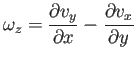
Deformación de cizalladura
La deformación de cizalladura, o de corte (shear strain), tiene tasas asociadas
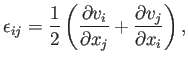
donde
Dilatación
La tasa asociada a la dilatación, definida
como el cambio relativo de la longitud de la partícula
en la dirección ![]() resulta ser
resulta ser
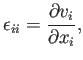
es decir, la componente
Tensor de deformación
Por tanto, se puede definir un tensor conjunto para la tasa de cizalladura-dilatación. Este tensor cumple las propiedades que pueden esperarse de un tensor de segundo orden simétrico. En particular, existen tres invariantes: la traza, el determinante, y una cantidad adicional. En términos de los autovalores del vector (llamados ``tasas de deformación principales'') las expresiones para estas cantidades son muy sencillas:
También puede definirse un tensor ![]() que sea el
gradiente de la velocidad (también llamada la jacobiana2.3) con componentes:
que sea el
gradiente de la velocidad (también llamada la jacobiana2.3) con componentes:
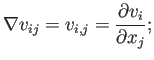
en notación tensorial sería un producto directo de dos vectores:
Es interesante que siempre podemos dividir el tensor en una parte simétrica y otra antisimétrica
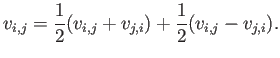
Es fácil comprobar que esto equivale a
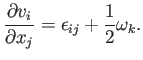
Es decir, las derivadas espaciales de la velocidad se deben a deformaciones de cizalladura y dilatación, más un término de rotación, que rota la partícula pero no la distorsiona. (Este término sólo está presente si
Más adelante utilizaremos la parte simetrizada del tensor gradiente
de velocidades,
![]() :
:
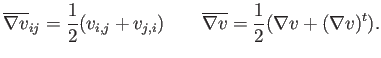
Daniel Duque 2011-11-10