Siguiente: Otros métodos de máxima Subir: Trabajo futuro Anterior: Base física para los Índice General
Aunque es, en principio, imposible determinar la forma que van a tener las funciones base en los métodos LME y SME, es cierto que, por lo general siguen siendo ``campanas''. Como no tienen soporte compacto es por lo tanto tentador aproximarlas por gaussianas. Por supuesto, se perderían todas las propiedades de consistencia de las funciones SME (incluyendo la de orden cero), pero si en la práctica se consigue a cambio convergencia a orden cero, primero y segundo, esto justificaría el procedimiento.
El ajuste sería sencillo, ya que conocemos el valor de la función de
forma ![]() en el nodo
en el nodo ![]() , así como sus primeras y segundas
derivadas. La Ecuación (A.14) para
, así como sus primeras y segundas
derivadas. La Ecuación (A.14) para ![]() (es decir,
(es decir, ![]() )
se reduce a:
)
se reduce a:
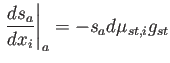 |
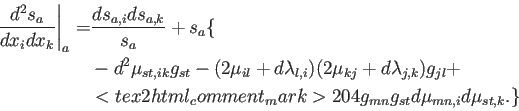 |
donde
Una vez determinadas las gaussianas aproximadas, todas las integrales que aparecen en un tratamiento de Galerkin (con masa acumulada o no) se evalúan muy fácilmente. Por lo que sabemos, no se han planteado nunca métodos de Galerkin basados en funciones gaussianas. Este método es bastante sencillo de analizar; evitamos dar aquí los detalles, pero el resultado final resulta ser casi idéntico a la expresión SPH directa, ec. (5.4), que justamente se evita por sus malas propiedades.
Daniel Duque 2011-11-10