Siguiente: Ajuste por gaussianas Subir: Trabajo futuro Anterior: Aplicar lo desarrollado Índice General
No hemos hecho énfasis apenas en una serie de requisitos físicos que una teoría de partículas debería verificar. Por una lado está la conservación de diversas magnitudes físicas en la simulación de la parte sin viscosidad (parte denominada a veces ``conservada'') de las ecuaciones de movimiento para las parículas:
Por otro lado, la parte viscosa (o ``no conservada'') debe satisfacer, además:
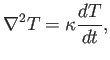
donde
Por desgracia, el método SME en la implementación ``directa'' 7.1 no satisface esta propiedad, como hemos verificado numéricamente. Tampoco satisface, como es obvio, la reciprocidad de acción y reacción, ya que, en general:
En cambio, una formulación como en los elementos finitos sí la satisface:
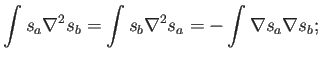
las dos primeras expresiones son iguales porque al integrar por partes se llega a una expresión manifiestamente simétrica (siempre que se puede integrar con partes; puede que las condiciones de contorno compliquen este argumento). También es sencillo demostrar que la expresión es semi-definida negativa. Esto significa que el laplaciano podría introducirse a la manera de elementos finitos con las funciones base SME, que es lo que se hace en el artículo original [33]. Sin embargo, nos gustaría evitar esta evaluación por los motivos enumerados en 7.1.
También hay que mencionar la importancia del programa GENERIC en el desarrollo de estas ideas, comenzando con el artículo seminal Ref. [1]. Este programa establece matemáticamente un marco de teorías que cumplen las propiedades mencionadas, y además permite enlazar correctamente con el nivel mesoscópico, en el cual están presentes fluctuaciones brownianas. Es importante tratar que la teoría resultante se adapte a esta estructura en lo posible.
Daniel Duque 2011-11-10