SPH

Este método fue propuesto en 1977 de manera casi simultánea por Lucy [15] y Gingold y Monaghan [16]. Fue la segunda referencia la que lo bautizó con el término con que se conoce hoy en día, hidrodinámica de partículas suavizadas (Smoothed Particle Hydrodynamics, SPH).

La idea era utilizar las técnicas de dinámica molecular, bastante bien asentadas por aquel entonces, para atacar problemas de hidrodinámica. La mecánica molecular, en resumen, consiste en resolver las ecuaciones de movimiento de Newton para un conjunto de moléculas. Sus ``partículas'' son, por tanto, centros de interacción móviles descritos por magnitudes físicas moleculares, microscópicas. Por ejemplo: masa, carga, momento dipolar; pero nunca presión ni viscosidad. La ventaja de el programa SPH es la relativa facilidad de implementar un método lagrangiano de este modo. Por ejemplo, no requiere ningún mallado (si acaso, y por motivos de eficacia numérica, una simple lista de vecinos que se utiliza a la hora de calcular las interacciones).

El método introduce una función nucleo (kernel) $W$ para describir las interacciones entre partículas. Esta función tiene por lo general forma de campana, es isotrópica, y se anula para puntos lejanos (tiene ``soporte compacto''). El alcance de esta función es muy importante.

La manera más natural de obtener una formulación SPH dentro del formalismo genérico de la sección 4.3.1 es a partir de una definición de volumen de una partícula

$$\frac{1}{\mathcal{V}_a} = \sum_b W(r_{ab}) ,$$

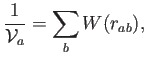
donde $r_{ab}=\vert r_a-r_b\vert$ . Las funciones núcleo tienen por tanto dimensiones de inversa de volumen.

Si una partícula $a$ tiene numerosas vecinas $b$ dentro del soporte de su núcleo, entonces el sumatorio tendrá un valor elevado y su volumen será pequeño. Si, por el contrario, no hay ninguna, el sumatorio sólo tendrá el término $a=b$ y el volumen será muy grande (este límite identifica además $w(0)$ como la inversa del volumen mínimo de una partícula).

Utilizando esta definición de volumen en la ecuación general de la divergencia (4.7) se llega directamente a esta expresión:

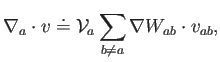$$\nabla_a\cdot v \doteq \mathcal{V}_a \sum_{b\ne a} \nabla W_{ab} \cdot v_{ab},$$ (4.16)

donde se quiere decir

$$\nabla W_{ab}=\nabla W (r_{ab})$$

y $v_{ab}$ es la velocidad relativa de las partículas $a$ y $b$ :

$$v_{ab}=v_a-v_b .$$

De hecho, se han propuesto diversas definiciones de la divergencia en SPH, y esta correspondería a una de ellas, muy similar a los discutidos en el artículo de referencia de Monaghan [5] (es idéntica a una de ella si las masas de las partículas son iguales, $m_a=m_b$ ; también puede deducirse exactamente si en la ecuación (2.13) de esta referencia se usa $\Phi=1/\mathcal{V}$ ).

En cuanto al gradiente, la ecuación genérica (4.15) se puede escribir así:

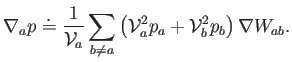$$\nabla_a p \doteq \frac{1}{\mathcal{V}_a} \sum_{b\ne a} \left( \mathcal{V}_a^2 p_a+ \mathcal{V}_b^2 p_b \right) \nabla W_{ab} .$$ (4.17)

Esta expresión es casi idéntica a la recomendada por Monaghan [17,5] (para ser precisos, las masas deben ser iguales para que se recupere exactamente la misma expresión).

Estas expresiones pueden servir de partida para desarrollar un método de simulación completo, que requiere atender numerosos detalles, entre otros:

La ecuación de estado.

Para cerrar el sistema de ecuaciones, se debe relacionar presión y densidad. Como las aplicaciones suelen ser hidrodinámicas, el sistema debe ser incompresible. Así pues, la ecuación de estado debe presentar una subida drástica de la presión con la densidad (se suele utilizar la de ecuación de Cole, que es muy sencilla). Alternativamente, se puede intentar implementar una incompresibilidad rigurosa, lo cual conlleva bastantes dificultades técnicas.

Derivadas de orden superior.

Por lo general, el laplaciano no se implementa como la divergencia del gradiente, ni tampoco se utilizan derivadas segundas del núcleo; por el contrario, se emplean otras expresiones equivalentes en teoría pero muchos más fáciles de implementar en la práctica (tan complicadas como las expresiones anteriores para la divergencia y el gradiente).

Las condiciones de contorno.

Como los nucleos de las partículas se extienden bastante, y son isotrópicos por lo general, las condiciones de contorno son complicadas de implementar.

Integración temporal.

Aunque no presenta ni mucho menos las dificultades de la integración espacial (al ser el tiempo unidimensional, y no estar discretizado de ninguna manera concreta), lo cierto es que es necesario hacer que el sistema evolucione en el tiempo con un algoritmo que tenga caraterísticas adecuadas. Por ejemplo, integradores simplécticos, como el de Verlet en alguna de sus variantes.

No es este el lugar para una discusión de todos estos aspectos del método SPH, ni de sus múltiples aplicaciones. Como se ha dicho, el método es, con gran diferencia, el más utilizado para simulaciones lagrangianas. Existe una fuerte comunidad académica que emplea este método. Por ejemplo, la ERIC (European Research Interest Group, Grupo de Interés de Investigación Europeo) SPHERIC, dentro de la comunidad ERCOFTAC (Europear Research Community On Flow, Turbulence, and Combustion) aglutina 12 grupos directivos (Steering Comitee), 52 grupos europeos adicionales y 23 de fuera de Europa. Cada año organiza un taller sobre el método, en cuyas dos últimas convocatorias el candidato ha presentado comunicaciones (en sesiones de ``teorías alternativas'') [18,19]. Las aplicaciones industriales también cabida en este grupo, con diversos grupos del campo de la hidráulica, energía, geología, obras públicas y explosivos.

La aplicación más existosa del método es, sin duda, en el campo de los efectos especiales. El programa informático RealFlow, desarrollado por la compañía Next Limit, es hoy en día el más destacado a la hora de desarrollar efectos realistas de líquidos. La compañía recibió un Premio de la Academia por Logros Técnicos (de la Academia de las Artes y las Ciencias Cinematográficas de EEUU) por su trabajo en El Señor de los Anillos, donde se simulaba agua y otros fluidos, como lava. Sin embargo, la compañía al parecer no utiliza SPH, sino otro método (mallado de Boltzmann) para su programa de simulación ingenieril XFlow.

Quizá esto último represente un punto de vista extendido: a pesar de la potencia y simplicidad de SPH, parece difícil ir ``más allá'' con él, y llegar hasta un desarrollo y aplicación comparables a los métodos de dinámica de fluidos computacional basados en mallas eulerianas. El método debe ser, por tanto, refinado considerablemente de manera apropiada para cada aplicación. Los recursos informáticos pueden ser, además, bastante intensivos si se requiere precisión: una carecterística de SPH es que se puede aumentar la preción aumentando el alcance del núcleo. Esto es por un lado positivo, ya que al menos existe esta posibilidad; pero un núcleo muy extendido amplía el número de vecinas de cada partícula, aumentando considerablemente el coste de la simulación en términos de tiempo de ejecución y también de memoria.

Una alternativa es considerar otros métodos basados en partículas, aprovechando las lecciones aprendidas de SPH (que son numerosas, en particular en lo relativo a los detalles técnicos mencionados arriba). Un enfoque muy interesante, pero que no desarrollaremos en detalle aquí, es aplicar ideas del método de los volúmenes finitos. Referimos al interesante trabajo de V. Springel [20].