next up previous contents
Siguiente: Dos dimensiones Subir: Convergencia del laplaciano Anterior: Convergencia del laplaciano   Índice General

Una dimensión

De manera similar a lo explicado en la sección 5.2, en una dimensión colocaremos $ N$ partículas sobre el segmento $ [0,1]$ en estas posibles disposiciones:

Nuestra función prueba es

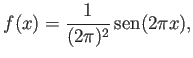
$\displaystyle f(x)=\frac{1}{(2\pi)^2} \sen(2 \pi x) , $

que cumple las condiciones de Dirichlet homogéneas $ f(-1/2)=f(1/2)=0$ . Su laplaciano exacto es

$\displaystyle g(x)=f''(x)= - \sen(2 \pi x). $

Discutimos tanto los resultados de aplicar el método de elementos finitos completo,

$\displaystyle \vec{g} \doteq m^{-1} \Lambda \vec{f}, $

como el de masa acumulada,

$\displaystyle \vec{g} \doteq m_0^{-1} \Lambda \vec{f}. $

Este último es muy rápido computacionalmente al no requerir inversión matricial.

En la figura 5.3 vemos los resultados de aplicar los dos métodos en una malla regular para $ N=10$ . El acuerdo es claramente excelente, incluso para este número tan bajo. En 5.4, con el mismo $ N$ pero con posiciones al azar, se aprecia que el resultado no es tan bueno. Las partículas que están muy alejadas causan grandes desviaciones respecto del valor exacto, en ambas versiones. En esta distribución en particular, existe un gran vacío de partículas en la parte izquierda del segmento, y ambas versiones fallan, como es natural. Sin embargo, la versión de masa acumulada parece fallar también en zonas con alta concentración de partículas, mientras que la completa no. Esto se debe a la multiplicación por la matriz $ m$ , que suaviza estas fluctuaciones.

Figura: Laplaciano aproximado por el método FEM en la versión completa (círculos azules) y de masa acumulada (cuadrados rojos) para partículas equiespaciadas en una dimensión. En línea continua negra, la solución exacta.
\includegraphics[width=0.5\textwidth]{fem_lapl_1d_sen}

Para cuantificar la convergencia, utilizaremos el error $ L_2$ relativo:

$\displaystyle L_2=\sqrt{\frac{\sum \left(g(x_a)-g_a\right)^2}{\sum \left(g_a\right)^2} }.$ (5.3)

En la figura 5.5 se muestra esta magnitud para el caso regular y aleatorio. En el primer caso se observa una clara convergencia de las dos versiones del método, con resultados casi indistinguibles en la escala empleanda. Un ajuste a una ley de potencia revela una convergencia como $ L_2\sim N^{-2}$ . En el caso aleatorio, en cambio, las dos versiones se distinguen claramente; la de masa completa sigue convergiendo con el mismo exponente $ -2$ , pero la de masa acumulada converge más lentamente, como $ L_2\sim N^{-1}$ .

Figura: Igual que en la figura 5.3, pero para distribución al azar de partículas.
\includegraphics[width=0.5\textwidth]{fem_lapl_1d_sen_ran}

Para completar el estudio, dibujamos también la convergencia del problema inverso (de Poisson):

$\displaystyle \vec{g} \doteq \Lambda^{-1} m \vec{f}, $

o, en versión de masa acumulada,

$\displaystyle \vec{g} \doteq \Lambda^{-1} m_0 \vec{f}. $

En la figura 5.6 se ve que las aproximaciones convergen; esta vez hay poca diferencia entre las dos, y obtenemos un ajuste aproximado a la ley $ L_2\sim N^{-2.4}$ . Es decir, la convergencia es mejor que en problema directo.

Figura: Convergencia del laplaciano aproximado por el método FEM. Círculos azules: versión completa en disposición aleatoria; diamantes azules: versión completa en disposición regular; cuadrados rojos: versión de masa acumulada en disposición aleatoria; cruces rojas: versión de masa acumulada en disposición regular. Las líneas azules son ajustes a los puntos mediante leyes de potencia de exponente $ -2$ ; la línea roja, ajuste mediante ley de potencia de exponente $ -1$ .
\includegraphics[width=0.5\textwidth]{fem_lapl_1d_l2}

Figura 5.6: Convergencia del problema de Poisson aproximado por el método FEM. Símbolos como en 5.5.
\includegraphics[width=0.5\textwidth]{fem_lapl_1d_l2_2}

next up previous contents
Siguiente: Dos dimensiones Subir: Convergencia del laplaciano Anterior: Convergencia del laplaciano   Índice General
Daniel Duque 2011-11-10