Dificultades

En la referencia[23], Mar Serrano informaba de que esta implementación fallaba parcialmente en una prueba muy sencilla: un campo externo de cizalla con forma sinusoidal. Más adelante, en la referencia [14] Pep Español y la misma autora analizaban las expresiones para los operadores diferenciales, dejando de lado por claridad las simulaciones hidrodinámicas completas. Se consideraban partículas dispuestas sobre el cuadrado unidad (tanto aleatoria como regularmente), en las cuales se imponía el campo

$$P(r) = P_0 \sen(k \cdot r)$$

(no se dice en el artículo, pero creemos que $P_0=1$ y $k=2\pi$ ). Se evalúa el gradiente según la fórmula 5.2, y se compara con el exacto,

$$g(r) = P_0 k \cos(k \cdot r) \vec{u}_x$$

mediante un error $L_1$ :

$$L_1=\frac{1}{N} \sum_a \vert (\nabla P)_a - g(r_a)\vert .$$

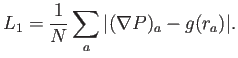
En la figura 5.2 se representa, a la izquierda, los resultados para distribuciones regulares y aleatorias. Como es de esperar, la convergencia es más lenta en el segundo caso, pero el operador diferencial converge adecuadamente.

La sorpresa aparece al hacer lo análogo para la divergencia. Primero se impone un campo vectorial

$$v(x,y) = v_0 \sen(k \cdot r)$$

cuya divergencia es

$$d(x,y) = v_0\cdot k \cos(k \cdot r) .$$

El error converge igual de bien en distribuciones regulares, pero la convergencia se destruye totalmente en distribuciones al azar. Este resultado es un auténtico obstáculo para una simulación de partículas. Incluso si se consigue una formulación que no involucre la divergencia, lo cual es bastante viable, el laplaciano que aparece en el término viscoso se verá forzosamente ``contaminado'' por la divergencia. Esto es obvio si éste se evalúa como la divergencia del gradiente. Por supuesto, todavía puede simularse un fluido inviscible, como se hace en la Ref. [21], ya que en la ecuación de Euler no aparece la viscosidad

Figura 5.2: Convergencia de los operadores gradiente (izquierda) y divergencia (derecha) para partículas al azar en dos dimensiones. Se dibuja el error $L_1$ en función de la distancia promedio entre partículas $h=1/\sqrt{N}$ , en escalas logarítmicas. De [14].