Ejercicios

1.

Usando el análisis de regresión, encuentra un modelo simplificado para la función que a un número k le asigna el k-ésimo número primo.

• Genera una serie de datos de longitud K con pares de datos (k, p), donde p es el primo k-ésimo.
• Ajusta una curva del tipo , con un parámetro libre a.

Referencia: teorema del numero primo.

2.

La sucesión de Collatz, o del 3*n+1, que ya vimos, consiste en aplicar sucesivamente la siguiente regla:

• Si un número es par, el siguiente número de la secuencia es n/2.
• Si es impar, el siguiente número de la secuencia es 3n+1.

El siguiente argumento heurístico muestra que la sucesión de Collatz debería converger a velocidad exponencial: partiendo de un número impar, lo multiplicamos por 3 (ignoramos el 1 que sumamos), y lo dividimos por la mayor potencia de 2 que lo divide hasta obtener otro número impar. ¿Cuál es la mayor potencia de 2 que divide a un número par? Bueno, depende del número, pero en promedio nos encontramos con un múltiplo de 4 la mitad de las veces (la otra mitad de las veces es de la forma 4n+2), con un múltiplo de 8 la cuarta parte de las veces, etcétera. Es decir, es seguro que podremos quitar el primer factor 2, pero cada factor sucesivo lo quitaremos con probabilidad 1/2^k. Dividir por 2 con probabilidad 1/2 viene a ser como dividir por 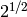. En resumen, hemos multiplicado nuestro número por:

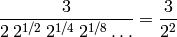
Siguiendo esta heurística,el j-ésimo punto de la sucesión de Collatz que comienza en k será 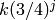, y el tiempo que tarda la sucesión en alcanzar 1 (llamémoslo T(k)) será aproximadamente .

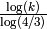Ajusta una curva T(k) = a log(k) a datos obtenidos calculando la sucesión para distintos valores de k.

3. El peligro del sobreajuste (overfitting)

Ante los datos siguientes, un investigador decide hacer un ajuste lineal. El objetivo es predecir qué pasará cuando x valga 10.

x:    0,    1,    2,    3,    4,     5
y: 1.03, 3.19, 5.10, 7.20, 9.10, 10.87

Ajusta los datos a un modelo lineal y usa el modelo para predecir el valor de y cuando x=10.

sage: datos = [[0,1.03], [1,3.19], [2,5.1], [3,7.2], [4,9.1], [5,10.87]]

Con los mismos datos de arriba, otro investigador decide usar como modelo un polinomio de grado 4 (con cinco grados de libertad) para conseguir un mejor ajuste. Realiza el ajuste, y predice un nuevo valor cuando x valga 10.

Como verás, el resultado obtenido es bastante menos razonable que el obtenido con el modelo lineal más sencillo. Si dibujas el nuevo modelo ajustado a los datos en un intervalo más grande verás por qué: los términos polinómicos son muy sensibles a los errores, y aunque la curva se ajusta mejor a los datos conocidos, ajusta peor los datos nuevos. No es buena idea introducir términos innecesarios en un modelo.

http://es.wikipedia.org/wiki/Sobreajuste

4. Predecir el tiempo que tardará un algoritmo

Uniendo las técnicas del bloque IV con el análisis de regresión podemos predecir el tiempo que tardará un algoritmo en ejecutarse.

La función calculo de abajo tiene complejidad cuadrática. Tu misión es estimar el tiempo que tardará en ejecutarse cuando la llamemos con el valor K=10000, usando como información los tiempos que tardó al ejecutarla con valores menores.

• Mide los tiempos de ejecución para los valores 1000, 2000, 3000, 4000 y 5000.
• Asume que el tiempo se ciñe al modelo: T=a*K^2.
• Ajusta el modelo a los datos obtenidos en el primer paso
• Usa el modelo para predecir el valor de T cuando K es 10000

Cuando hayas terminado, mide el tiempo de ejecución y comprueba si el modelo es adecuado.

sage: def calculo(K):
...       lista = []
...       for j in range(K):
...           lista.insert(0,j)

5. Alometría

La siguiente serie de datos está extraída de un artículo de biología en el que se estudia el diámetro del ojo de un animal (D) como función de su peso (P). Usamos sólo los datos de los primates.

datos =[[0.3300, 12.544],
[4.1850, 17.278],
[2.9000, 17.979],
[0.2000, 12.938],
[167.5000, 22.500],
[72.3416, 24.521],
[9.2500, 17.599],
[6.0000, 19.176],
[51.5000, 19.000],
[19.5100, 19.750],
[0.1150, 8.070]]

.

• Dibuja los datos. Intenta pensar qué tipo de curva podría ajustar esos datos: ¿bastará un modelo lineal?
• Ajusta un modelo del tipo “D = a*P^b”, con dos parámetros a y b .
• Define dos nuevas variables: U = log(P) y V=log(D). Transforma los datos de las variables (P,D) en datos para las variables (U,V).
• Ajusta un modelo lineal en el que U sea la variable independiente y V la variable dependiente.
• Deduce a partir de ese modelo un modelo para P y D. Dibuja ese modelo. En este problema, el resultado es bastante similar al obtenido con el método anterior.