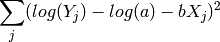El análisis de regresión consiste en encontrar un modelo que relaciona los valores medidos de un conjunto de variables.
Los valores medidos en el mundo real nunca se ajustan de forma perfecta a un modelo, debido en primer lugar a errores de medida, pero también a que cualquier modelo matemático es una simplificación del mundo real, y si tuviera en cuenta todos los factores que influyen en un conjunto de variables, sería inmanejable.
Por tanto, no tiene sentido aspirar a encontrar un modelo que prediga exactamente los valores medidos, y debemos admitir que el modelo cometerá un cierto error.
Un modelo útil encuentra una relación funcional sencilla en conjuntos de pocas variables. Se trata de explicar una variable que tiene importancia para nosotras, en función de otro conjunto de variables mejor conocidas o más fáciles de medir. El análisis de regresión (más exactamente, el análisis de regresión paramétrico ) permite encontrar un modelo explicativo en tres etapas:
- Nuestro conocimiento del tema en cuestión nos permite escribir un modelo que afirma que la variable X es una función de las variables
. La variable X recibe el nombre de variable dependiente y las variables
- Tomamos una muestra . Es decir, medimos todas las variables en un subconjunto de todos los casos posibles (unos cuantos individuos de la población, unos cuantos momentos de tiempo, una cuantas muestras preparadas en el laboratorio...)
- Ajustamos el modelo , eligiendo aquellos valores de los parámetros tales que la distancia entre los valores medidos de la variable X y los valores predichos aplicando el modelo minimizan el error cometido.
Tratamos de predecir la temperatura a la que hierve el agua ( T ), conocida la presión atmosférica ( P ) en el lugar y momento en que hacemos el experimento.
Para ello, contamos con un conjunto de mediciones de ambas variables, con la temperatura en grados Fahrenheit y la presión en pulgadas de mercurio (sea lo que sea, es una unidad de medidad de presión). Por ejemplo, en un cierto punto de los Alpes, un cierto día, el barómetro marcaba 20.79 pulgadas de mercurio, y el agua hirvió a 194.5 grados Fahrenheit. Las mediciones se realizaron en el mismo lugar geográfico, pero en días distintos, con distintas condiciones atmosféricas y quizá incluso por personas distintas. En estas condiciones, es imposible que ningún modelo prediga con exactitud el valor de T en función de P, pero esperamos que lo haga con un margen de error moderado.
T P
194.5 20.79
194.3 20.79
197.9 22.4
198.4 22.67
199.4 23.15
199.9 23.35
200.9 23.89
201.1 23.99
201.4 24.02
201.3 24.01
203.6 25.14
204.6 26.57
209.5 28.49
208.6 27.76
210.7 29.04
211.9 29.88
212.2 30.06
Referencia: http://www.sci.usq.edu.au/staff/dunn/Datasets/Books/Hand/Hand-R/alps-R.html
Comenzamos por dibujar los datos:
sage: datos = [(20.79,194.50),(20.79,194.30),(22.40,197.90),(22.67,198.40),
... (23.15,199.40),(23.35,199.90),(23.89,200.90),(23.99,201.10),
... (24.02,201.40),(24.01,201.30),(25.14,203.60),(26.57,204.60),
... (28.49,209.50),(27.76,208.60),(29.04,210.70),(29.88,211.90),
... (30.06,212.20)]
sage: puntos = point(datos)
sage: puntos.show(axes_labels=('Presion','Temperatura'))
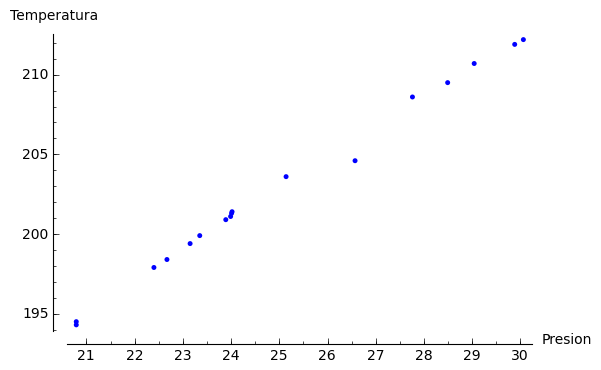
Los datos parecen estar dispuestos sobre una recta, de modo que intentamos un modelo lineal, de la forma:
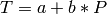
A priori, no conocemos los valores de a y b . Para unos valores fijos de a y b , cometeremos un error en la medición j-ésima que será exactamente: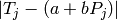 
. Vemos que no existe un criterio unívoco para encontrar a y b , dado que no existe ninguna recta que pase por todos los pares 
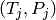. Para cualquier elección de **a* y b , nuestro modelo cometerá un error al estimar alguno de los puntos medidos.
Podemos escoger los valores de a y b para los que el error máximo cometido es menor, o aquellos para los que el error medio cometido es menor, o según otros muchos criterios. Es bastante habitual en estadística buscar los valores de a y b que hacen mínimo el error cuadrático total :
La función find_fit de SAGE permite ajustar un modelo cualquiera de tal forma que se minimice el error cuadrático. La función acepta dos argumentos: los datos y el modelo.
- Los datos deben ser una lista con todas las mediciones. Cada elemento de la lista es una lista o tupla con los valores de las variables en una medición. La última variable es la variable dependiente.
- El modelo es una función simbólica de varias variables que representan las variables independientes y de otras variables que representan los parámetros del modelo.
Aparte, acepta otros valores opcionales como parameters y variables para indicar a find_fit cuál es la variable dependiente y cuáles son los parámetros del modelo (más información en la documentación de find_fit ).
sage: var('T P a b')
(T, P, a, b)
sage: #Importante: marcamos nuestro modelo como dependiente de la variable P
sage: #El resto de variables simbólicas se toman como parametros
sage: modelo(P) = a + b*P
sage: #find_fit devuelve los valores de los parametros
sage: #que minimizan el error cuadratico
sage: #Al pasar el argumento solution_dict=True,
sage: #devuelve los valores optimos como un diccionario
sage: parametros = find_fit(datos, modelo, solution_dict=True)
sage: print parametros
{b: 1.9017835212187804, a: 155.29648352710586}
sage: #Sustituimos los valores de a y b en el modelo
sage: modelo_ajustado = modelo.subs(parametros)
sage: print modelo_ajustado
sage: #Dibujamos los puntos originales y la recta a+b*P
sage: ajuste = plot(modelo_ajustado,(P,20,30),rgbcolor=(0,1,0))
sage: grafica = puntos + ajuste
sage: grafica.show(axes_labels=('Presion','Temperatura'))
P |--> 1.9017835212187804*P + 155.29648352710586
Hemos establecido el modelo:
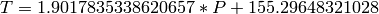
Ahora podemos utilizarlo para predecir la temperatura a la que hervirá el agua a una cierta presión.Por ejemplo, esperamos que si un día la presión es de 24.5 mmHg, el agua hervirá a:
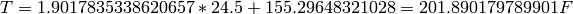
sage: modelo_ajustado(P=24.5)
201.890179796966
No es difícil demostrar que los parámetros que minimizan el error cuadrático en un modelo lineal son únicos. Sin embargo, cuando usamos modelos no lineales, puede haber varios mínimos de la función de error cuadrático total. En general, la minimización es más complicada, y puede que el algoritmo no consiga encontrar los valores óptimos de a y b sin ayuda. Esta vez no vamos a usar datos reales, sino datos generados usando números aleatorios. Se trata de ver qué tal ajustamos un modelo en un caso en el que conocemos cómo fueron generados los datos.
Obtenemos los datos usando la fórmula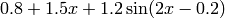 
, y sumando un número aleatorio extraído según una distribución normal de media 0 y varianza 0.1:
sage: #Fijamos una semilla de numeros aleatorios para asegurar
sage: #que todas obtenemos el mismo resultado
sage: set_random_seed(123)
sage: datos = [(i, 0.8+1.5*i+1.2*sin(2*i-0.2) + 0.1*normalvariate(0,1))
... for i in srange(0, 4*pi, 0.4)]
sage: puntos = point(datos)
sage: puntos.show(axes_labels=('x','y'))
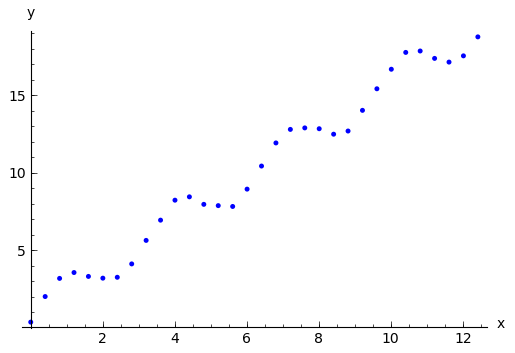
Tratamos ahora de ajustar a estos datos un modelo del tipo:
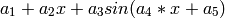
sage: var ('a1,a2,a3,a4,a5,x')
sage: modelo(x) = a1+a2*x+a3*sin(a4*x-a5)
sage: show(modelo(x))
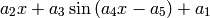
sage: parametros = find_fit(datos, modelo, solution_dict=True)
sage: print parametros
Warning: Number of calls to function has reached maxfev = 1200.
{a3: 97.399974374571215, a2: -4.6922665568748858, a1: 36.856991032455262, a5: -5.9092115507119871, a4: 0.064311341301833705}
sage: modelo_ajustado = modelo.substitute(parametros)
sage: print modelo_ajustado
x |--> -4.6922665568748858*x + 97.399974374571215*sin(0.064311341301833705*x + 5.9092115507119871) + 36.856991032455262
sage: g_ajuste = plot(modelo_ajustado(x), (x,0,4*pi), color='red')
sage: grafica = puntos + g_ajuste
sage: grafica.show(axes_labels=('x','y'))
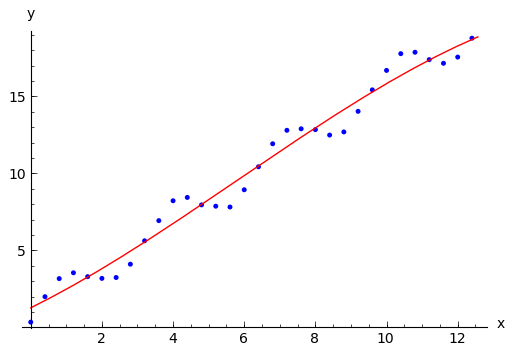
La minimización del error se ha quedado atascada por el camino. La forma más sencilla de ayudar al algoritmo es darle un punto de partida mejor . Para ello, pasamos a find_fit un argumento adicional: initial_guess . También le pasamos los argumentos parameters y variables para que sepa cuáles de las variable simbólicas del modelo son los parámetros.
sage: #Ejercicio: prueba con distintos valores iniciales
sage: #para tratar de conseguir un mejor ajuste
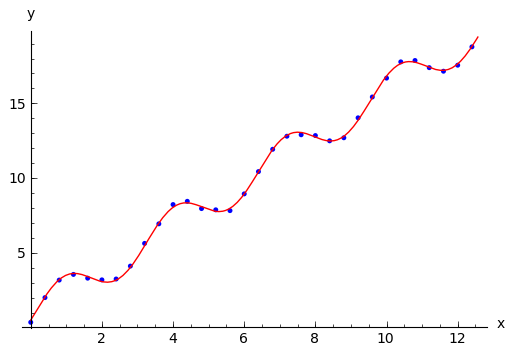
sage: parametros = find_fit(datos, modelo, initial_guess=[0,0,1.0,2,0],
... parameters=[a1,a2,a3,a4,a5], variables=[x], solution_dict=True)
sage: print parametros
{a3: 1.2403261721812324, a2: 1.5056455458784646, a1: 0.78272474105136614, a5: 0.23540896442811415, a4: 2.001600272362738}
sage: modelo_ajustado = modelo.substitute(parametros)
sage: print modelo_ajustado
x |--> 1.5056455458784646*x + 1.2403261721812324*sin(2.001600272362738*x - 0.23540896442811415) + 0.78272474105136614
sage: g_ajuste = plot(modelo_ajustado(x), (x,0,4*pi), color='red')
sage: grafica = puntos + g_ajuste
sage: grafica.show(axes_labels=('x','y'))
Vamos a resolver un ejemplo de laboratorio.
En un estudio sobre la resistencia a bajas temperaturas del bacilo de la fiebre tifoidea, se expusieron cultivos del bacilo durante diferentes periodos de tiempo a -5 grados C. Los siguientes datos representan:
X = tiempo de exposición (en semanas).
Y = porcentaje de bacilos supervivientes.
Nuestro objetivo es predecir el valor de Y conocido el valor de X.
sage: datos= [(0, 100), (0.5, 42), (1, 14), (2, 7.5), (3, 0.4), (5, 0.11),
... (9, 0.05), (15, 0.002)]
sage: puntos= point(datos)
sage: show(puntos)
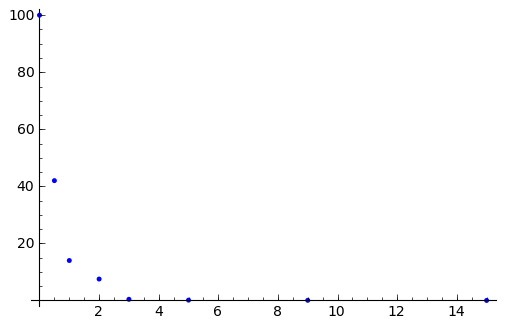
Ajustar una recta (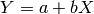
) y una exponencial (
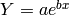) a los datos: ¿qué ajuste es mejor?
La forma clásica de ajustar un modelo exponencial entre dos variables X e Y es reducirlo a un ajuste lineal entre las variables X y V=log(Y).
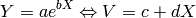
para c=log(a), d=b. La razón para usar este enfoque es que el ajuste lineal se puede realizar fácilmente con una calculadora, mientras que el ajuste de un modelo no lineal requiere de una computadora.
Si dibujamos las variables X y V juntas vemos que parece sensato que estén relacionadas por un modelo lineal.
sage: datosXV = [(d[0],log(d[1])) for d in datos]
sage: show(point(datosXV))
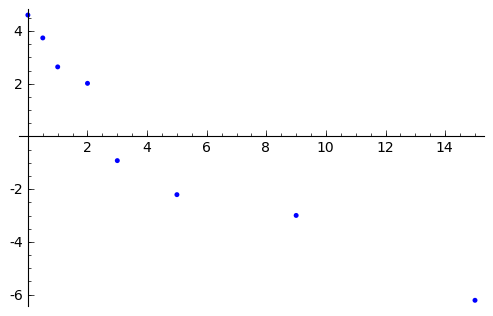
Ajusta un modelo lineal con X como variable independiente y V como variable dependiente. Deduce un modelo para escribir Y en función de X, y dibújalo junto a los datos.
Observamos que las dos curvas exponenciales no se parecen gran cosa. La razón es que no es lo mismo minimizar el error cuadrático:
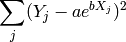
que el error cuadrático después de tomar logaritmos:
