Criptografía RSA¶

El objeto de la criptografía es poder comunicarse con otras personas encriptando nuestros mensajes de tal modo que si alguien encuentra el mensaje codificado no sepa lo que dice, pero que si el mensaje llega a su destino, esa persona pueda recuperar el mensaje original. Por ejemplo, podemos cambiar todos los usos de la palabra tanque por la palabra paloma , para que quien encuentr el mensaje piense que hablamos de otra cosa. Hoy vamos a estudiar algunos métodos matemáticos para encriptar mensajes basados en la teoría de números.

Codificar un mensaje de texto en números¶

Para poder aplicar estos métodos criptográficos, tenemos que codificar la información que queremos mandar como una secuencia de números enteros. Por ejemplo, podemos hacer corresponder un número a cada posible letra. Para no preocuparnos de la codificación de carateres, usaremos un alfabeto simplificado, y el código de cada letra será la posición que ocupa en el alfabeto.

sage: #nuestro alfabeto son el espacio en blanco y las mayusculas sin acentos
sage: alfabeto=' ABCDEFGHIJKLMNOPQRSTUVWXYZ'
sage: L=len(alfabeto)
sage: def codifica_letra(letra):
...       return alfabeto.index(letra)
sage: def decodifica_letra(n):
...       return alfabeto[n]

sage: codifica_letra('A')
1

sage: decodifica_letra(1)
'A'

Ejercicio : Usa la función ord para implementar codifica_letra con menor complejidad.

Y ahora para una cadena del tirón

sage: def codifica_cadena(texto):
...       return [codifica_letra(c) for c in texto]
...
sage: def decodifica_cadena(lista):
...       return ''.join([decodifica_letra(j) for j in lista])

sage: texto = 'HOLA MUNDO'
sage: codifica_cadena(texto)
[8, 15, 12, 1, 0, 13, 21, 14, 4, 15]

sage: decodifica_cadena([8, 15, 12, 1, 0, 13, 21, 14, 4, 15])
'HOLA MUNDO'

Cifrado de César¶

Para ejecutar el cifrado de César de clave k , sustituimos cada letra del mensaje original por la letra que está k posiciones a la derecha (dando la vuelta al alfabeto si nos pasamos de largo). Por ejemplo, si k=3 :

CENA -> FHPD

Para implementar este método criptográfico, tomamos una cadena de caracteres, la codificamos en una secuencia de números, le sumamos k a cada código, tomamos el resto de dividir por la longitud del alfabeto y después decodificamos los números en letras para volver a tener una cadena de caracteres.

sage: L=len(alfabeto)
sage: def cesar(texto, k):
...       '''Cesar...
...       '''
...       numeros = codifica_cadena(texto)
...       encriptado = [(j+k)%L for j in numeros]
...       texto_encriptado = decodifica_cadena(encriptado)
...       return texto_encriptado

sage: print cesar(texto,0)
sage: print cesar(texto,1)
sage: print cesar(texto,2)
HOLA MUNDO
IPMBANVOEP
JQNCBOWPFQ

Encriptación RSA¶

En el sistema RSA, un número menor que N (que puede representar texto, o cualquier otra cosa), se encripta elevándolo a un exponente módulo N . La operación de desencriptado también usa la misma operación, pero con un exponente distinto. Aunque podríamos usar la misma función para las tareas de encriptar y desencriptar, preferimos usar dos funciones distintas por claridad.

Encriptado¶

Cada número de la secuencia se eleva al exponente e módulo N . Por tanto, para encriptar se necesita el par formado por N y e , que llamaremos la clave pública.

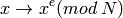
$x\rightarrow x^e (mod\; N)$

Desencriptado¶

Cada número de la secuencia se eleva al exponente d módulo N . Para desencriptar se necesita el par formado por N y d , que llamaremos la clave privada.

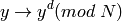
$y\rightarrow y^d (mod\; N)$

sage: def encripta_RSA(lista,N,e):
...       '''Encripta una secuencia de numeros siguiendo el metodo RSA'''
...       return [power_mod(numero,e,N) for numero in lista]
...
sage: def desencripta_RSA(lista,N,d):
...       '''Desencripta una secuencia de numeros siguiendo el metodo RSA'''
...       return [power_mod(numero,d,N) for numero in lista]

Por ejemplo, usamos de forma naive el método RSA para encriptar el código de cada letra del mensaje.

sage: texto = 'HOLA MUNDO'
sage: p=29; q=31;
sage: N=p*q
sage: e=13
sage: d=517
sage: clave_publica=(N,e)
sage: print texto
sage: numeros = codifica_cadena(texto)
sage: encriptado = encripta_RSA(numeros, N, e)
sage: print encriptado
HOLA MUNDO
[47, 27, 389, 1, 0, 879, 301, 524, 312, 27]

sage: desencriptado = desencripta_RSA(encriptado, N, d)
sage: texto_desencriptado = decodifica_cadena(desencriptado)
sage: print texto_desencriptado
HOLA MUNDO

Análisis de frecuencias¶

Si usamos una misma clave de cifrado para un texto lo bastante largo, eventualmente encontramos repeticiones. En los dos cifrados anteriores, una misma letra se codifica siempre a la misma letra. Estudiando las frecuencias de aparición de cada carácter, podemos averiguar cosas sobre la clave de cifrado. Por ejemplo, si en un texto en castellano encriptado con el cifrado de César al letra más repetida es la ‘D’, probablemente la clave sea 3, que se la que lleva la ‘A’ (la letra más frecuente en la mayoría de textos en castellanos) en la ‘D’. En el cifrado RSA letra a letra, descifrar el texto es sólo ligeramente más difícil.

Veremos más sobre este punto en el ejercicio a entregar.

Agrupar varios números pequeños en uno grande¶

Para tener esperanzas de conseguir un cifrado resistente al análisis de frecuencias, tenemos que agrupar los códigos de varias letras en un sólo número más grande.

La tarea de codificación consta por tanto de dos partes:

Sustituir cada carácter por su código numérico, de la misma forma que hicimos antes.

Agrupar un bloque de varios números en un sólo número más grande. El sistema es similar al usado cuando nos daban una lista con los dígitos de un número y teníamos que recuperar el número. A una secuencia $\{n_1,\dots,n_b\}$ de números entre 0 y L-1 le hacemos corresponder un número entre 0 y $L^{b}-1$ :

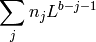
$\sum_j n_j L^{b-j-1}$

sage: def bloque2numero(bloque):
...       numero = 0
...       for k in bloque:
...           numero = numero*L + k
...       return numero
sage: bloque2numero([1,1])
28

sage: mensaje='EN UN LUGAR DE LA MANCHA'
sage: letras = [codifica_letra(letra) for letra in mensaje]
sage: print letras
[5, 14, 0, 21, 14, 0, 12, 21, 7, 1, 18, 0, 4, 5, 0, 12, 1, 0, 13, 1, 14, 3, 8, 1]

sage: #Agrupamos las letras
sage: b=3
sage: n = len(letras)
sage: bloques = [letras[i:i+b] for i in range(0,n,b)]
sage: print bloques
[[5, 14, 0], [21, 14, 0], [12, 21, 7], [1, 18, 0], [4, 5, 0], [12, 1, 0], [13, 1, 14], [3, 8, 1]]

sage: codigo = [bloque2numero(bloque) for bloque in bloques]
sage: print codigo
[4023, 15687, 9322, 1215, 3051, 8775, 9518, 2404]

Encapsulamos la codificación en una función:

sage: def codifica_mensaje(mensaje,b):
...       '''Convierte una secuencia de letras en una secuencia de numeros
...       El espacio en blanco se codifica como 0, las letras a partir de 1
...       Las letras se agrupan en bloques de b letras
...       '''
...       letras = [codifica_letra(letra) for letra in mensaje]
...       #rellenamos con espacios en blanco al final
...       letras = letras + [0]*(b-len(letras)%b)
...       n = len(letras)
...       #Agrupamos en bloques
...       bloques = [letras[i:i+b] for i in range(0,n,b)]
...       #cambiamos cada bloque por un numero
...       codigo = [bloque2numero(bloque) for bloque in bloques]
...       return codigo

sage: mensaje='CITA EN EL PATIO'
sage: codifica_mensaje(mensaje,2)
[90, 541, 5, 378, 147, 16, 47, 258, 0]

Las operaciones inversas son similares, ahora tenemos que recuperar el texto a partir de la secuencia de números:

Convertir los números entre 0 y $L^{b}-1$ en bloques de b números entre 0 y L .

Poner los números de cada bloque unos a continuación de otros.

Sustituir los números por los caracteres con esos códigos.

Convertir la lista de caracteres en una cadena de caracteres usando join .

sage: def decodifica_letra(n):
...       return alfabeto[n]
sage: def numero2bloque(n,b):
...       bloque=[]
...       for i in range(b):
...           bloque.append(n%L)
...           n=n//L
...       bloque.reverse()
...       return bloque
sage: def decodifica_mensaje(secuencia,b):
...       '''Convierte una secuencia de numeros en una secuencia de letras
...       '''
...       bloques=[numero2bloque(numero,b) for numero in secuencia]
...       numeros=[]
...       for b in bloques:
...           numeros.extend(b)   #extiende numeros con los numeros del bloque b
...       letras=[decodifica_letra(k) for k in numeros]
...       mensaje=''.join(letras)
...       return mensaje

sage: decodifica_mensaje([90, 541, 5, 378, 147, 16, 47, 258],2)
'CITA EN EL PATIO'

Uniendo los pasos de codificar un texto y encriptarlo, componemos estas dos funciones que trabajan directamente con una cadena de caracteres y una clave RSA.

sage: def encripta_mensaje(mensaje, clave_publica):
...       '''Encripta una cadena de texto siguiendo el metodo RSA
...       clave_publica es la tupla formada por N y e
...       '''
...       N,e = clave_publica
...       b   = floor( log(N)/log(L) )
...       mensaje_codificado = codifica_mensaje(mensaje,b)
...       mensaje_encriptado = encripta_RSA(mensaje_codificado,N,e)
...       return mensaje_encriptado
sage: def desencripta_mensaje(secuencia, clave_privada):
...       '''Desencripta una cadena de texto siguiendo el metodo RSA
...       clave_privada es la tupla formada por N y d
...       '''
...       N,d=clave_privada
...       b=floor( log(N)/log(L) )
...       mensaje_codificado = desencripta_RSA(secuencia,N,d)
...       mensaje_decodificado = decodifica_mensaje(mensaje_codificado,b)
...       return mensaje_decodificado

Un ejemplo con números pequeños¶

Para que las operaciones de encriptado y desencriptado sean inversas una de la otra, se tiene que verificar, para cualquier x :

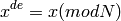
$x^{de}=x(mod N)$

Los números siguientes tienen esta propiedad, así que al desencriptar deberíamos recuperar el mensaje original. El número N es el producto de dos números primos p y q .

sage: p=29; q=31;
sage: N=p*q
sage: e=13
sage: d=517
sage: clave_publica=(N,e)
sage: mensaje_encriptado=encripta_mensaje(mensaje, clave_publica)
sage: print mensaje_encriptado
[193, 90, 470, 378, 449, 252, 66, 474, 0]

sage: clave_privada=(N,d)
sage: desencripta_mensaje(mensaje_encriptado,clave_privada)
'CITA EN EL PATIO  '

Generar pares de clave pública y privada¶

Veamos ahora cómo encontrar pares de clave pública y privada arbitrariamente grandes. Necesitamos números N , e y d tales que

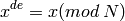
$x^{de}=x(mod\; N)$

para cualquier 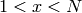$1<x<N$ , pero además no debe ser fácil encontrar d a partir de e :

Tomamos N igual al producto de dos primos muy grandes.

Buscamos e que sea primo con $\phi(N)=(p-1)(q-1)$ .

Gracias al paso anterior, existe el número d , inverso de e módulo $\phi(N)$ .

Gracias al teorema de Euler : $x^{de}=x(mod\; N)$ para cualquier $x$ .

sage: #Generar aleatoriamente dos primos grandes
sage: tamanyo = 1e30
sage: K=randint(tamanyo,2*tamanyo)
sage: p=next_prime(K)
sage: K=randint(tamanyo,2*tamanyo)
sage: q=next_prime(K)
sage: N=p*q
sage: print p,q,N
1903561781303804650708611174377 1413802211606170528899700267741 2691259856336300529650100032902971489570304620017251338872357

Escoge un exponente e que sea invertible módulo 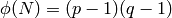$\phi(N)=(p-1)(q-1)$ :

sage: phi = (p-1)*(q-1)
sage: e = randint(1,phi)
sage: while gcd(e,phi)>1:
...       e = randint(1,phi)
sage: print e
1028828637415512438195946182018372770826935014622750450108039

Invierte el exponente e módulo 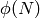$\phi(N)$ :

sage: d=inverse_mod(e,phi)
sage: print d
2404689434731437327767913609076829006215515438918314901998999

Comprobamos que todo ha salido bien encriptando un mensaje y luego desencriptándolo. Usamos un alfabeto más grande para poder encriptar un texto más largo.

sage: #La u delante de la cadena indica que contiene caracteres internacionales
sage: #codificados en el estandar unicode
sage: alfabeto = u''' abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~\t\n\x0b\x0c\r0123456789áéíóúñ'''
sage: L=len(alfabeto)

sage: cable=u'''C O N F I D E N T I A L MADRID 000593
sage: SIPDIS
sage: STATE FOR EUR/WE AND EEB/TPP/IPE
sage: STATE PASS USTR FOR JGROVES AND DWEINER
sage: STATE PASS U.S. COPYRIGHT OFFICE
sage: USDOC FOR 4212/DCALVERT
sage: USDOC ALSO FOR PTO
sage: E.O. 12958: DECL: 06/19/2014
sage: TAGS: KIPR, SP
sage: SUBJECT: NEW CULTURE MINISTER ON FIGHT AGAINST INTERNET
sage: PIRACY
sage: REF: A. STATE 42723
sage: B. MADRID 129
sage: Classified By: CdA Arnold A. Chacon, for Reason 1.4(d)
sage: 1.(C) Summary and Action Requests: New Culture Minister
sage: Gonzalez-Sinde, a committed opponent of internet piracy,
sage: updated the Charge on the status of negotiations between
sage: content providers and ISPs. She welcomed a shift in approach
sage: by content providers that would have the GOS seek legal
sage: changes allowing it to block offending web pages. After
sage: several months, participants would review the results to see
sage: whether other action (e.g., action against individual users),
sage: was needed. The Minister reacted enthusiastically to our
sage: offer of expert engagement, saying it would be valuable for
sage: GOS officials to hear what has worked and what has not worked
sage: to reduce illicit downloads. Post requests that Washington
sage: agencies seek to provide experts to discuss this issue with
sage: GOS officials in visits or through video conferences. Post
sage: also requests that Washington agencies respond favorably to
sage: the Minister's interest in involving U.S. experts in
sage: IPR-related events during Spain's EU presidency next year.
sage: End Summary and Action Requests.
sage: '''

sage: numeros=encripta_mensaje(cable, (N,e))
sage: print numeros
[1781525537726156920438311978041211784455389532455800628604290, 138654119902188225868408341012879259393616750148143296188396, 2019372767622323851892807364861138235702600816789036033252999, 1285011671605935272210742418778085319364089218477171375202944, 358818263139892406583186382860022046715759719591641259330315, 1991024227028606884075565970070590882708417602783544863933961, 2343320689832869489365244054535568356319333420468094703050911, 246986225067867018135808716773609339600989477341784041328592, 295062511579974632800956190119466781154091535208020730499977, 1385766328947880270767009714670941834332446286351155274963656, 2219806433167952790783356714421514445706625024211159815928006, 319966925667769159444679534604648333449705169614066972028467, 2453254760438113539224926123435386450302049015975229129209459, 586537927652003422034998741731777227844305679654330626168941, 1547051151503790222360071635662831283116257915351028037023228, 1386240724211415866814333115387605951388737026841613292527098, 2415453740479606884130473800755044032473299776597760792622733, 1745659575192698570411945083184906511450670790192381316376514, 2313942017048439345557198222853619270934903916517516397356372, 2064274122214832956162674907770722614480161967835719637619675, 1070933801445530749801620493496857437803404618386824467056431, 1802146806781477610550042026950111284440924727170799007393342, 1838525451382949139715369181098671252646370989194133730355378, 707024284916037578397628228248104381756304175065156524657577, 846584051878373563365263837085390171308281985178646086748886, 976813914662260397318447227001032128302804047413344913340286, 2566842249490006371994134706473314972916478359143725288036695, 216366296188304313358636812167962011827637201379551199837521, 1454659381381492215721099780235133378767775952737225411143563, 1792695569740475104135567955491398463118629436282499995619067, 388319614832977949439997504061019573215835397399483967944308, 2299976007557252519174275097793671704390554718221378551414354, 950260964263272019460627808949769408233403528145126313170941, 910420315370250696187492030877510389422094866778294928252377, 1676176713067368480703702893819253411041123055977782540271935, 860275928172593799549758203794397214027685242603163691858420, 2273580957289029179395379568003612707699011557696156427077476, 2405296492396829217181987299404867970726392152313799974430988, 1905820380840257404905810309342142141886713075928724078300406, 1804956565849211064602107936548952936617015405170299208708138, 1941030521406761021271519029918303904698160741873431976086009, 1814499089871344087010551748434831857451384169946312607999276, 865792652304926327687451975045152211647620110216410247005611, 1946966815380761076349970413611795937387810418489924481642214, 529939816303736995924269755824463858954266245278504841909448, 1710317756506979595098359842476099742637282270240185943975130, 1301549154642747286633414256414404959176538051946904637209075, 1967139196519701758160212193967675893661419037984445680718831, 105997400726834897307929521209315430066633738587429664885115, 1320704091566359197666691328049707083894466688174429939432489]

sage: #Deberiamos recuperar el mensaje original, aunque los
sage: #caracteres unicode se ven un poco distintos
sage: print desencripta_mensaje(numeros,(N,d))
C O N F I D E N T I A L MADRID 000593

SIPDIS

STATE FOR EUR/WE AND EEB/TPP/IPE
STATE PASS USTR FOR JGROVES AND DWEINER
STATE PASS U.S. COPYRIGHT OFFICE
USDOC FOR 4212/DCALVERT
USDOC ALSO FOR PTO

E.O. 12958: DECL: 06/19/2014
TAGS: KIPR, SP
SUBJECT: NEW CULTURE MINISTER ON FIGHT AGAINST INTERNET
PIRACY

REF: A. STATE 42723
B. MADRID 129

Classified By: CdA Arnold A. Chacon, for Reason 1.4(d)

1.(C) Summary and Action Requests: New Culture Minister
Gonzalez-Sinde, a committed opponent of internet piracy,
updated the Charge on the status of negotiations between
content providers and ISPs. She welcomed a shift in approach
by content providers that would have the GOS seek legal
changes allowing it to block offending web pages. After
several months, participants would review the results to see
whether other action (e.g., action against individual users),
was needed. The Minister reacted enthusiastically to our
offer of expert engagement, saying it would be valuable for
GOS officials to hear what has worked and what has not worked
to reduce illicit downloads. Post requests that Washington
agencies seek to provide experts to discuss this issue with
GOS officials in visits or through video conferences. Post
also requests that Washington agencies respond favorably to
the Minister's interest in involving U.S. experts in
IPR-related events during Spain's EU presidency next year.
End Summary and Action Requests.

La seguridad del sistema RSA se basa en que calcular la clave privada en función de la clave pública requiere mucho tiempo de cómputo. Pero si conocemos la factorización de N, conocemos el número 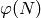$\varphi(N)$ , y podemos calcular el exponente de desencriptado.

El pilar del sistema es que factorizar números grandes lleva mucho más tiempo de cómputo que encontrar números primos grandes. Si dedicamos un poco más de tiempo a buscar números primos un poco más grandes, el tiempo necesario para factorizar el producto de los números aumenta en una proporción mucho mayor.

sage: %time
sage: tamanyo = 1e10
sage: K=randint(tamanyo,2*tamanyo)
sage: p=next_prime(K)
sage: K=randint(tamanyo,2*tamanyo)
sage: q=next_prime(K)
sage: N=p*q
sage: print p,q,N
11434278431 11245017313 128578658918257475903
CPU time: 0.00 s,  Wall time: 0.00 s

sage: %time
sage: factor(N)
11245017313 * 11434278431
CPU time: 0.01 s,  Wall time: 0.10 s

sage: %time
sage: tamanyo = 1e20
sage: K=randint(tamanyo,2*tamanyo)
sage: p=next_prime(K)
sage: K=randint(tamanyo,2*tamanyo)
sage: q=next_prime(K)
sage: N=p*q
sage: print p,q,N
167630755805843746343 163492503135211998401 27406371869144865602492332625985565597543
CPU time: 0.00 s,  Wall time: 0.00 s

sage: %time
sage: factor(N)
163492503135211998401 * 167630755805843746343
CPU time: 0.24 s,  Wall time: 0.59 s

sage: %time
sage: tamanyo = 1e30
sage: K=randint(tamanyo,2*tamanyo)
sage: p=next_prime(K)
sage: K=randint(tamanyo,2*tamanyo)
sage: q=next_prime(K)
sage: N=p*q
sage: print p,q,N
1775360778775552738367426329231 1551261724291569068929331402687 2754049222922986839254015328851480115307288059642380700043697
CPU time: 0.03 s,  Wall time: 0.02 s

sage: %time
sage: factor(N)
1551261724291569068929331402687 * 1775360778775552738367426329231
CPU time: 17.48 s,  Wall time: 17.93 s

Criptografía RSA¶

Codificar un mensaje de texto en números¶

Cifrado de César¶

Encriptación RSA¶

Encriptado¶

Desencriptado¶

Análisis de frecuencias¶

Agrupar varios números pequeños en uno grande¶

Un ejemplo con números pequeños¶

Generar pares de clave pública y privada¶

Contenidos

Tema anterior

Próximo tema

Esta página

Navegación

Criptografía RSA¶

Codificar un mensaje de texto en números¶

Cifrado de César¶

Encriptación RSA¶

Encriptado¶

Desencriptado¶

Análisis de frecuencias¶

Agrupar varios números pequeños en uno grande¶

Un ejemplo con números pequeños¶

Generar pares de clave pública y privada¶

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Navegación