Hallar el vector gradiente, en cada punto en el que exista, de las siguientes funciones escalares
.
Calcular la distancia mínima entre los puntos de la gráfica de 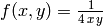 y el punto
y el punto 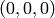 .
.
Calcula las derivadas parciales 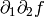 y
y 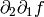 en el punto (0,0):
en el punto (0,0):
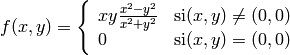
Decide si son iguales, y si son continuas en (0,0).
Nota: esta función muestra que el recíproco del teorema de Clairaut (tb llamado teorema de Schwartz) es falso: http://es.wikipedia.org/wiki/Teorema_de_Clairaut
Hallar los puntos críticos y determinar cuáles son los máximos locales, mínimos locales o puntos silla:
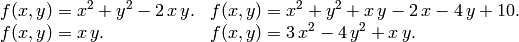
Investiga la ayuda de region_plot con el objetivo de dibujar la unión de dos regiones. Es posible que la calidad del dibujo empeore, pero la ayuda también explica cómo mejorar la precisión del dibujo.
En los siguientes apartados, se supone que la integral de una función positiva 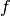 sobre la región
sobre la región 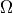 se reduce a la integral iterada que se da. En cada caso, se pide determinar y dibujar la región
se reduce a la integral iterada que se da. En cada caso, se pide determinar y dibujar la región  e invertir el orden de integración.
e invertir el orden de integración.
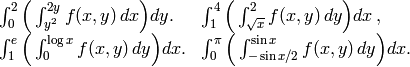
Indicación: usa region_plot para dibujar la región. Después de hacer el cambio en el orden de integración, dibuja de nuevo la región para comprobar que obtienes el mismo resultado.
Hallar el valor de las siguientes integrales, determinando y dibujando en cada caso el recinto de integración
, con
.
, siendo
la región limitada por los planos
.
, siendo
el sólido limitado por la superficie
y los planos
y
.
Veamos cómo realizar integrales de línea como las que aparecen en el teorema de Green. Este teorema se suele escribir así:
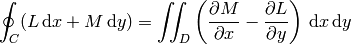
Con frecuencia, ésta es una manera práctica de evaluar integrales planas sobre regiones que no admiten una descomposición sencilla en regiones simples. Por ejemplo, podemos calcular áreas:
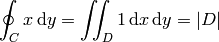
- Calcula el área de un triángulo con este método. Comprueba el resultado calculando el área de triángulos cuya área puedas calcular a mano.
- Calcula el área de un polígono de n lados.
- Demuestra que el área de la elipse es
es
Indicación: Recuerda que una parametrización de la elipse es 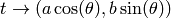 .
.