En esta hoja vamos a estudiar problemas de cálculo diferencial e integral en varias dimensiones espaciales. En general, manejaremos funciones de varias variables simbólicas.
Comencemos por representar gráficamente funciones de dos variables reales.
sage: var('x,y')
(x, y)
sage: f1 = sin((x+y)^2)
sage: f1.show()
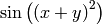
El comando plot3d genera una superficie cuya altura sobre el punto (x,y) es proporcional al valor de una función f de dos variables simbólicas. La sintaxis es:
plot3d(f,(x,x1,x2),(y,y1,y2))
- x e y son variables simbólicas
- f es función de x y de y
- (x1,x2) es el rango que se mostrará de la variable x
- (y1,y2) es el rango que se mostrará de la variable y
Al mostrar la gráfica llamando a show() , podemos pasar el argumento opcional viewer que nos permite elegir entre varias formas de mostrar la gráfica, algunas interactivas, que permiten girar la gráfica con el ratón. Como de costumbre, plot3d? y p.show? (p es una gráfica generada con plot3d ) muestran la ayuda con ejemplos de uso.
sage: p = plot3d(f1,(x,-1,1),(y,-1,1))
sage: p.show(viewer='tachyon')

sage: f2 = x*y*exp(x-y)
sage: f2.show()
sage: p = plot3d(f2,(x,-2,0.5),(y,-0.5,2))
sage: p.show(viewer='tachyon')
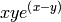

Otra opción es dibujar curvas de nivel de la función en el plano (x,y). Usando
implicit_plot(f,(x,x1,x2),(y,y1,y2))
Dibujamos la curva dada por f=0. Si pasamos a implicit_plot el argumento adicional contours, el dibujo contiene tantas curvas de nivel como le indiquemos:
implicit_plot(f,(x,x1,x2),(y,y1,y2), contours= 10)
ó exactamente las curvas de nivel que le indiquemos:
implicit_plot(f,(x,x1,x2),(y,y1,y2), contours = lista)
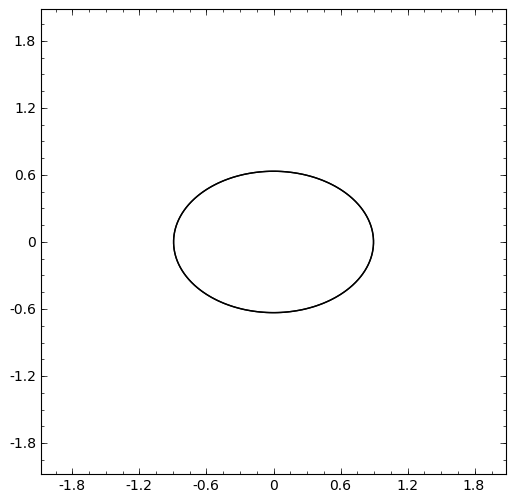
sage: #Pasando a show el parametro adicional aspect_ratio=1
sage: #garantizamos que se mantendrá el ratio correcto entre
sage: #el eje x y el eje y
sage: implicit_plot(x^2 + 2*y^2 - 0.8,(x,-2,2),(y,-2,2)).show(aspect_ratio=1)
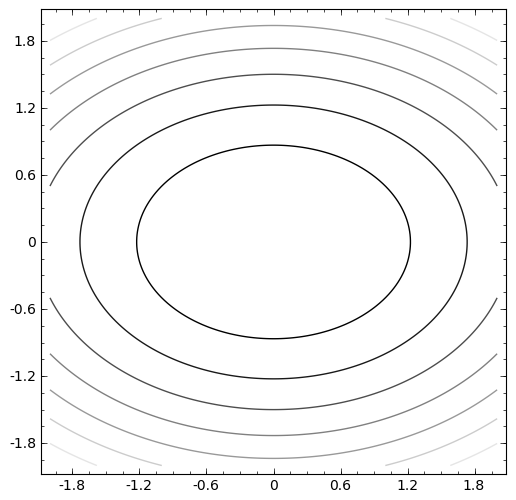
sage: implicit_plot(x^2 + 2*y^2,(x,-2,2),(y,-2,2),contours=10).show(aspect_ratio=1)
sage: implicit_plot(x^2 + 2*y^2,(x,-2,2),(y,-2,2),contours=srange(0,4,0.1)).show(aspect_ratio=1)
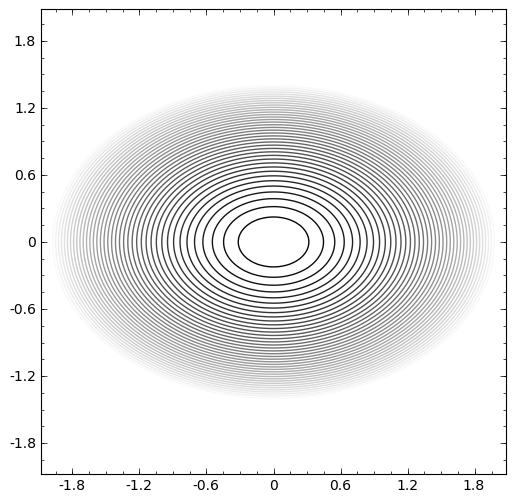
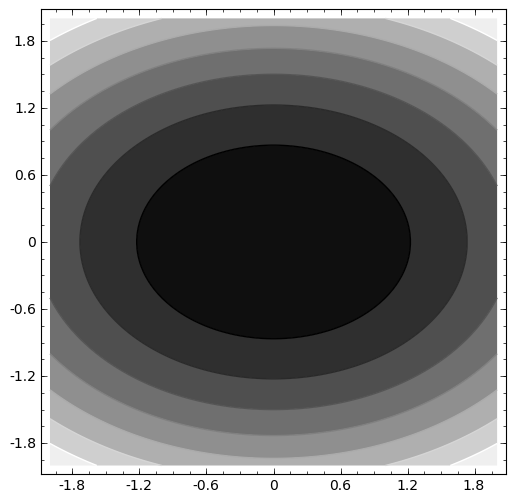
contour_plot es muy similar al anterior, pues muestra de distinto color la región entre dos curvas de nivel consecutivas (es decir, la preimagen de un intervalo).
sage: contour_plot(x^2+2*y^2,(x,-2,2),(y,-2,2)).show(aspect_ratio=1)
Comparamos las distintas formas de representar una función de dos variables.
sage: f3=log(2+sin(x*y))
sage: f3.show()
sage: plot3d(f3,(x,-3,3),(y,-3,3)).show(viewer='tachyon')
sage: contour_plot(f3,(x,-3,3),(y,-3,3)).show()
sage: implicit_plot(f3,(x,-3,3),(y,-3,3),contours=10).show()
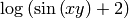
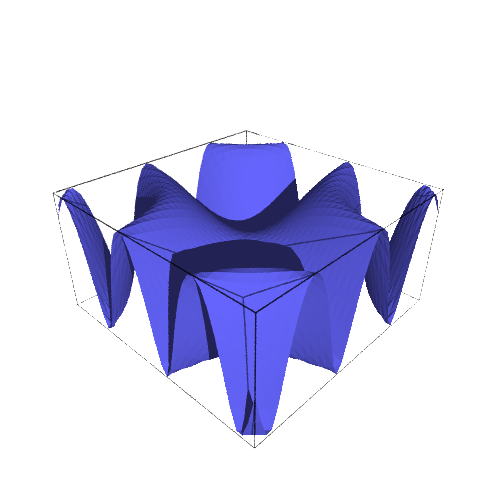
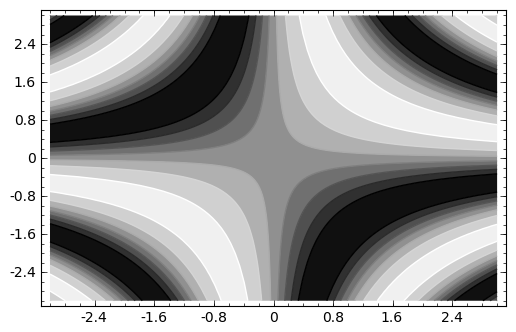
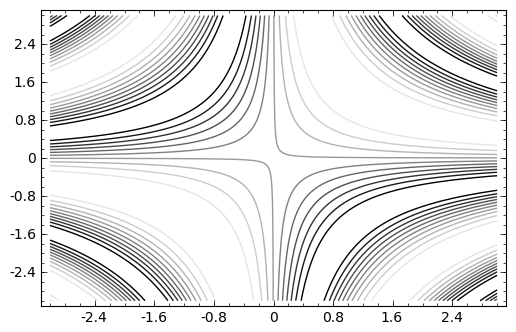
Una función de dos variables simbólicas se puede derivar respecto de cada una de ellas de forma independiente. De esta forma podemos aplicar la fórmula del plano tangente en un punto:
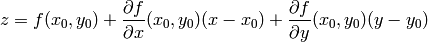
Las gráficas de curvas de nivel no permiten apreciar bien el plano tangente, pero podemos representar el plano junto a la función con plot3d .
sage: f4=x*log(x^2+y^2)
sage: f4.show()
sage: x0 = 1
sage: y0 = 1
sage: plano = (x - x0)*f4.derivative(x,1).subs(x=x0, y=y0) + (y - y0)*f4.derivative(y,1).subs(x=x0, y=y0) + f4(x=x0, y=y0)
sage: show(plano)
sage: p = (plot3d(f4,(x,-1.5,1.5),(y,-1.5,1.5)) +
... plot3d(plano,(x,-1.5,1.5),(y,-1.5,1.5),color='red') +
... point3d( (x0,y0,f4(x=x0,y=y0)), color='green', pointsize='30') )
sage: p.show(viewer='tachyon')
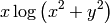
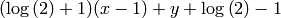

La fórmula del plano tangente es el caso particular de la fórmula del polinomio de Taylor de la función en un punto:
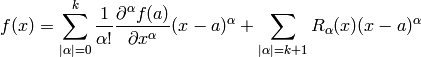
Donde 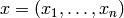 es una variable vectorial, y
es una variable vectorial, y 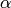 es un multiíndice. En palabras, el polinomio de Taylor de f de orden k en
es un multiíndice. En palabras, el polinomio de Taylor de f de orden k en 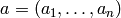 contiene todos los monomios construídos con derivadas de orden menor o igual que k. La sintaxis para construir el polinomio de Taylor de f de orden k en las variables (x,y) y en el punto (a,b) es:
contiene todos los monomios construídos con derivadas de orden menor o igual que k. La sintaxis para construir el polinomio de Taylor de f de orden k en las variables (x,y) y en el punto (a,b) es:
f.taylor((x,a),(y,b),k)
sage: #El polinomio de Taylor de orden 1 es la ecuacion del
sage: #plano tangente
sage: x0 = 1
sage: y0 = 1
sage: plano = (x - x0)*f4.derivative(x,1).subs(x=x0,y=y0) + (y - y0)*f4.derivative(y,1).subs(x=x0,y=y0) + f4(x=x0,y=y0)
sage: show(plano)
sage: f4t1 = f4.taylor((x,x0),(y,y0),1)
sage: show(f4t1)
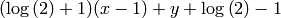
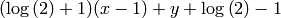
sage: f5 = x*exp(x + y)
sage: f5.show()
sage: pol5 = f5.taylor((x,0),(y,0),2)
sage: pol5.show()
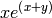
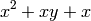
sage: p1=plot3d(f5,(x,-1,1),(y,-1,1));
sage: p2=plot3d(pol5,(x,-1,1),(y,-1,1),color='red');
sage: show(p1+p2,viewer='tachyon')
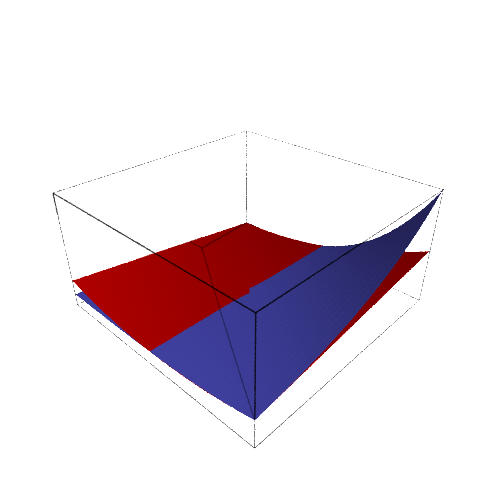
- Calcula la derivada direccional de la función
en el punto
y la dirección
.
- Investiga la ayuda del comando arrow, y dibuja el gradiente de f6 en un punto. Observa el efecto al cambiar la función, y el punto.
sage: f6=sin(x*y)+cos(x*y)
sage: f6.show()
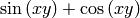
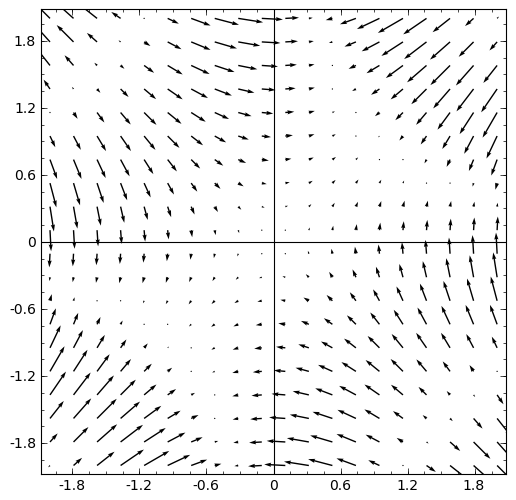
Usando el comando plot_vector_field , podemos dibujar el campo gradiente . El campo de vectores gradiente de f es la asignación del vector gradiente de f a cada punto del plano. Recordemos de las clases de teoría que el gradiente es perpendicular a las curvas de nivel. Es una buena ocasión para dibujar simultáneamente las curvas de nivel y el campo gradiente de una función.
sage: f7=sin(x*y)+cos(x*y)
sage: f7.show()
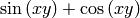
sage: plot_vector_field(f7.gradient(),(x,-2,2),(y,-2,2)).show(aspect_ratio=1)
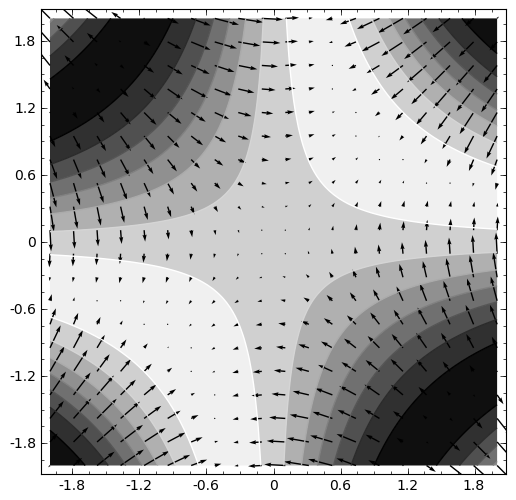
sage: (contour_plot(f7,(x,-2,2),(y,-2,2)) + plot_vector_field(f7.gradient(),(x,-2,2),(y,-2,2))).show(aspect_ratio=1)
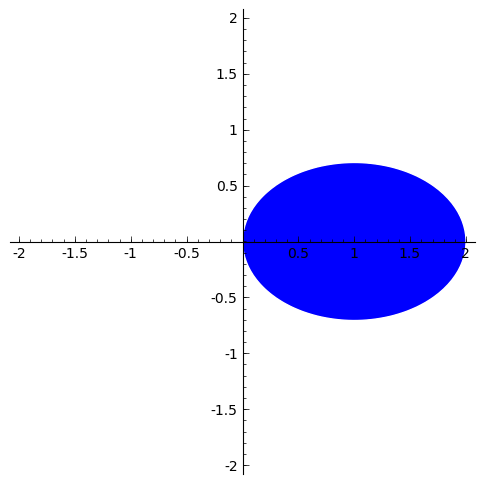
Otro comando interesante es el comando region_plot, que sirve para dibujar regiones definidas por desigualdades. Se puede llamar de varias formas para representar regiones definidas por varias ecuaciones (ver la ayuda para más información). En esta sesión lo usaremos para visualizar regiones de integración.
sage: #Una elipse
sage: region_plot((x-1)^2 + 2*y^2 < 1,(x,-2,2),(y,-2,2)).show(aspect_ratio=1)
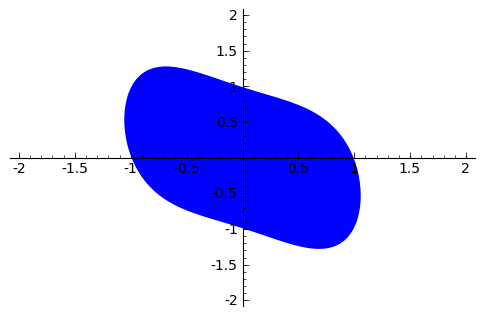
sage: #Un algo
sage: region_plot(x^4+x*y+y^2<1,(x,-2,2),(y,-2,2))
sage: #La interseccion de las dos regiones anteriores
sage: region_plot([x^4+x*y+y^2<1, (x-1)^2+2*y^2<1],(x,-2,2),(y,-2,2))
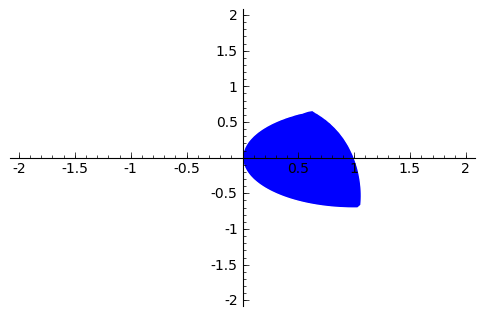
dibuja la región 0<=x<=1,x*(1-x)<=y<=sin(pi*x)
La forma más naive de buscar puntos críticos es resolver el sistema de ecuaciones no lineales
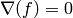
El sistema es trivial de plantear usando el método gradient visto antes, y podemos intentar resolver el sistema llamando a solve :
solve(list(f.gradient()),f.variables())
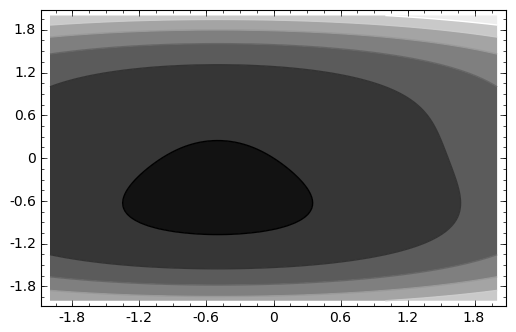
sage: #Esta funcion parece tener un minimo cerca de (-0.5,-0.5)
sage: var('x y')
sage: f = x^2 + y^4 + x + y
sage: contour_plot(f,(x,-2,2),(y,-2,2)).show()
sage: #Obtenemos varias soluciones "extra":
sage: #?Cual corresponde al minimo?
sage: solve(list(f.gradient()),f.variables())
[[x == -0.5, y == (0.314980262474 + 0.545561817986*I)], [x == -0.5, y == (0.314980262474 - 0.545561817986*I)], [x == -0.5, y == -0.629960578187]]
Por supuesto, con funciones más complicadas, este tipo de sistemas de ecuaciones no lineales es casi imposible de resolver.
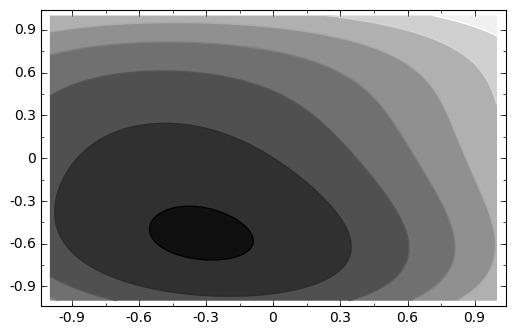
sage: #Esta funcion parece tener un minimo cerca de (-0.3,-0.5)
sage: var('x y')
sage: f = x^2+ y^4 + sin(x+y)
sage: contour_plot(f,(x,-1,1),(y,-1,1),plot_points=300).show()
sage: solve(list(f.gradient()),[x,y])
[2*x + cos(x + y), 4*y^3 + cos(x + y)]
El paquete scipy.optimize contiene varios métodos relacionados con problemas de optimización. El método scipy.optimize.fmin busca mínimos de una función de varias variables partiendo de un punto inicial. Para llamar al método, es necesario definir una función de python que acepta como argumento una lista con los valores de las variables y devuelve el valor de la función en el punto. El resultado es el mínimo propuesto, y una estimación del error cometido. Además, nos imprime un resumen de la ejecución del algoritmo numérico.
sage: from scipy.optimize import fmin
sage: def f_0(xs):
... x,y = xs
... return x^2 + y^4 + x + y
sage: fmin(f_0,(0,0))
Optimization terminated successfully.
Current function value: -0.722470
Iterations: 58
Function evaluations: 113
array([-0.500004 , -0.62998934])
sage: from scipy.optimize import fmin
sage: def f_0(xs):
... x,y = xs
... return x^2 + y^4 + sin(x + y)
sage: fmin(f_0,(0,0))
Optimization terminated successfully.
Current function value: -0.570485
Iterations: 60
Function evaluations: 109
array([-0.32318198, -0.54469709])
La integración simbólica sobre regiones cuadradas no supone ningún quebradero de cabeza (siempre que el sistema sea capaz de encontrar las integrales del integrando). Para calcular la integral doble, integramos primero respecto de una variable y después respecto de la otra.
Ejemplo:
![\iint_Q x^2\,e^y\,d x\,d y, \ Q=[-1,1]\times [0,\log 2]](_images/math/d220fde0f27d3f2b6b6a32bd62a462855cc827de.png)
sage: f = x^2*e^y
sage: f.integral(x,-1,1).integral(y,0,log(2))
2/3
Para regiones más generales, tenemos que operar igual que en clase de Cálculo, descomponiendo la región en subregiones del tipo:
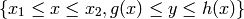
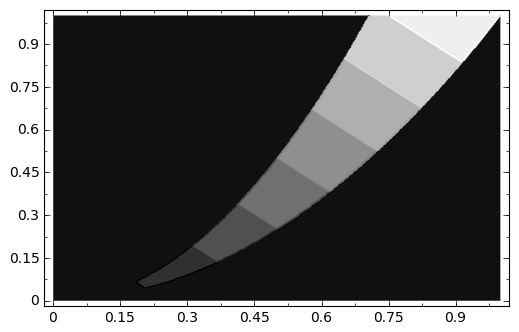
Representa el conjunto de los valores 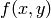 sobre
sobre ![Q=[0,1]\times [0,1]](_images/math/1ca9c03f35d67fae15f240f8a636452c69543e9a.png) y calcula el volumen del sólido así obtenido.
y calcula el volumen del sólido así obtenido.
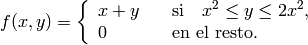
sage: #Comenzamos por dibujar la funcion
sage: #!!!Atencion!!! Esta vez el argumento de plot3d no es una
sage: #funcion de dos variables simbolicas, sino una funcion
sage: #normal de python que acepta como argumentos dos numeros
sage: #reales y devuelve otro
sage: def f(a,b):
... if a^2 <= b <= 2*a^2:
... return a+b
... else:
... return 0
sage: plot3d(f,(0,1),(0,1)).show(viewer='tachyon')

sage: #Un dibujo de curvas de nivel es igualmente ilustrativo
sage: contour_plot(f,(0,1),(0,1),plot_points=300).show()
sage: #para calcular la integral simbolica necesitamos definir
sage: #una funcion de dos variables simbolicas, pero debemos
sage: #integrar solo en la region adecuada
sage: var('x y')
sage: g = x + y
sage: print g
sage: print g.integral(y,x^2,2*x^2)
sage: print g.integral(y,x^2,2*x^2).integral(x,0,1)
x + y
3/2*x^4 + x^3
11/20
Cuando sea imposible evaluar la integral de una función sobre una región básica del plano de forma exacta, podemos hacerlo de forma numérica con scipy.integrate.dblquad
sage: #Es necesario importar la funcion dblquad
sage: #del paquete scipy.integrate al que pertenece
sage: from scipy.integrate import dblquad
sage: dblquad?
<html>...</html>
Calculamos la misma integral que calculamos antes de forma simbólica usando dblquad.
sage: def g(x,y):
... return x+y
sage: def gfun(x):
... return x^2
sage: def hfun(x):
... return 2*x^2
sage: dblquad(g,0,1,gfun,hfun)
(0.54999999999999993, 6.1062266354383602e-15)
Probemos a calcular una integral en coordenadas cartesianas y polares. Recordemos que:
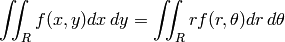
sage: var('x y r theta')
(x, y, r, theta)
sage: f = x^2+y^2
sage: print f.integral(y,-sqrt(1-x^2),sqrt(1-x^2)).integral(x,-1,1)
CODE:
sage47 : integrate(sage43,sage44,sage45,sage46)$
Maxima ERROR:
defint: lower limit of integration must be real; found -sqrt(1-x^2)
-- an error. To debug this try: debugmode(true);
Traceback (most recent call last):
...
TypeError: Error executing code in Maxima
El código anterior produce un error. Hurgando un poco en la traza del error, leemos:
TypeError: Error executing code in Maxima
CODE:
sage9 : integrate(sage5,sage6,sage7,sage8)
Maxima ERROR:
defint: lower limit of integration must be real; found \-sqrt(1\-x^2)
Recordemos que SAGE usa otras piezas de software con más tradición siempre que puede. En este caso, le pasa la tarea de realizar la integral a la librería Maxima . Esta librería arroja un error bastante ilustrativo: “el límite de integración debe ser real”, pero sqrt(1-x^2) puede ser imaginario. Entender la causa del error no siempre garantiza que se pueda superar el problema, pero en este caso la solución es informar a Sage de que puede asumir que x está entre -1 y 1.
En cualquier caso, nada nos garantiza el éxito al intentar una integral de forma simbólica, así que deberíamos estar preparadas para hacer la integral con dblquad si todo lo demás falla.
sage: assume(1-x^2>0)
sage: f = x^2+y^2
sage: print f.integral(y,-sqrt(1-x^2),sqrt(1-x^2)).integral(x,-1,1)
1/2*pi
sage: #Integramos en coordenadas polares.
sage: f_polar = f(x=r*cos(theta),y=r*sin(theta))
sage: print f_polar
sage: #Intentamos simplificar el integrando (no es necesario)
sage: f_polar = f_polar.full_simplify()
sage: print f_polar
sage: integrando_polar = r*f_polar()
sage: integrando_polar.integral(theta,0,2*pi).integral(r,0,1)
r^2*sin(theta)^2 + r^2*cos(theta)^2
r^2
1/2*pi