Ejercicios

1.

Estudia la función:

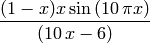
en el intervalo [0,1]:

• La función no está definida cuando x=0.6. Indica cómo puedes extender la función para que quede definida en ese punto, siendo continua si es posible.
• Encuentra todos sus máximos y mínimos locales y globales en ese intervalo.
• Dibuja la función en el intervalo [0,1], con los extremos locales indicados en un color y los extremos absolutos indicados en un color distinto.

2.

Estudia la función g:

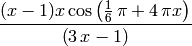
en el intervalo [0,1]

• Calcula la segunda derivada de g.
• Dibuja la segunda derivada de g en el intervalo [0,1], y encuentra todos los ceros de la segunda derivada.
• Dibuja la función en el intervalo [0,1], con los puntos encontrados antes marcados en rojo. Es decir, deben aparecer, dibujados sobre la gráfica de f, los puntos donde se anula la segunda derivada.

3.

Define en un cuadro de comandos una función f en la variable simbólica x y un valor x0 . A continuación, escribe código para:

• Calcular la función de la variable simbólica x que representa la recta tangente a f en el punto x0 , a partir de los datos anteriores.
• Dibujar la función cerca del punto, el punto (x0,f(x0)) en otro color, y la recta tangente a la función en (x0,f(x0)) en otro color.

sage: f(x) = sin(x)
sage: x0   = 0

4.

Escoge una función f(x) cuyo límite cuando 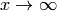exista, y crea una gráfica que muestre la función y la asíntota, en un rango aceptable de valores de x .

5.

Escoge una función con una asíntota oblicua, encuentra una función simbólica que represente esa asíntota y dibuja en la misma gráfica la función y la asíntota.

6.

Escoge una función convexa en un intervalo [a,b] y escribe código que, dado un número K, genere una gráfica que muestre la función en el intervalo, y K rectas tangentes a la función en puntos (x,f(x)) para puntos x equiespaciados en el intervalo [a,b] .

Repite el ejercicio para una función con un punto de inflexión.