Siguiente: Sobre este documento... Subir: Derivadas de las funciones Anterior: Primeras derivadas Índice General
Los resultados anteriores pueden encontrarse, con menos detalles, en la Ref. [33]. Lo que sigue representa material original.
Ahora deseamos calcular
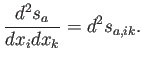 |
(A.28) |
Por la regla de la cadena, y tras algunos pasos intermedios,
Todas las expresiones que aparecen se han discutido en las secciones
anteriores, salvo las segundas derivadas espaciales
![]() and
and
![]() . Ahora, debemos imponer que la segunda derivada espacial de
la Ec. (A.8) siga siendo nula:
. Ahora, debemos imponer que la segunda derivada espacial de
la Ec. (A.8) siga siendo nula:
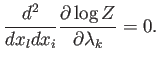 |
(A.30) |
De este modo, llegamos a
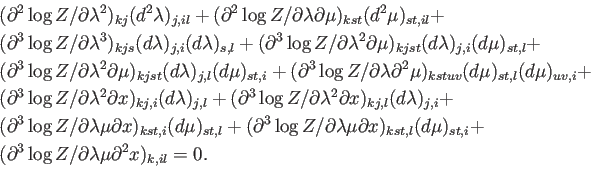 |
(A.31) |
Un resultado similar se sigue de
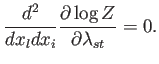 |
(A.32) |
De nuevo, llegamos a un problema de álgebra lineal que debe ser
resuelto. El ``vector'' de soluciones es ahora una matriz: cada
columna ![]() de ella corresponde a
de ella corresponde a
![]() ; el índice de fila
; el índice de fila
![]() corresponde a la dirección cartesiona
corresponde a la dirección cartesiona ![]() .
.
Para calcular las nuevas derivadas de ![]() que hacen falta, tenemos
el resultado general
que hacen falta, tenemos
el resultado general
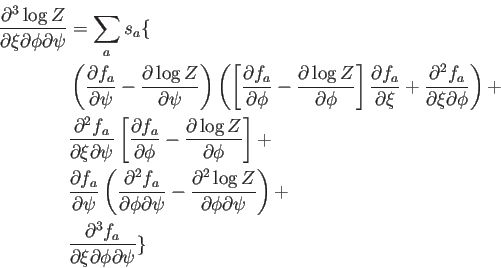 |
(A.33) |
De este modo, obtenemos las siguentes derivadas.
| (A.35) |
| (A.36) |
| (A.37) |
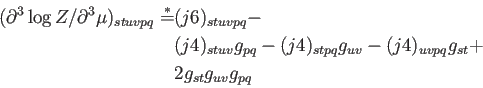 |
(A.38) |
| (A.39) |
![\begin{displaymath}\begin{split}(\partial^3 \log Z / \partial\lambda\partial\mu\...
..._{sk}+ \\ & 2\mu_{kl}[(j4)_{list} - g_{li} g_{st} ] \end{split}\end{displaymath}](img533.png) |
(A.40) |
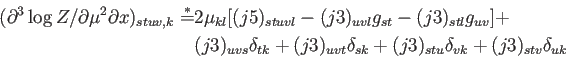 |
(A.41) |
| (A.42) |
Ahora el procedimiento sería:
Queremos recalcar que en estas expresiones suponemos que el tensor ![]() es constante en un entorno local del punto en cuestión, así que sus
derivadas espaciales no aparecen. Sin embargo, no hacemos ninguna otra
suposición adicional. Por ejemplo, si
es constante en un entorno local del punto en cuestión, así que sus
derivadas espaciales no aparecen. Sin embargo, no hacemos ninguna otra
suposición adicional. Por ejemplo, si ![]() es simplemente el tensor
identidad multiplicado con un escalar (que es justamente nuestra
elección), muchas de las expresiones se simplifican considerablemente.
es simplemente el tensor
identidad multiplicado con un escalar (que es justamente nuestra
elección), muchas de las expresiones se simplifican considerablemente.
Daniel Duque 2011-11-10