Consistencia redefinida

Sin embargo, esta función objetivo no lleva a nada nuevo. Para ser más precisos, la solución de la función objetivo siempre conducirá al límite $\beta \rightarrow \infty$ , es decir, la solución de elementos finitos sobre la triangulación de Delaunay hallada por Rajan. Existen dos maneras de explicar este hecho (que, desde luego, un cálculo numérico confirma inmediatamente).

La primera, que se puede encontrar en [31] y [33] (más detallada en el segundo), es de origen geométrico. En particular, se desarrolla en el ``espacio de la solución'': un espacio $d+1$ formado por los nodos y los valores de cierta función definida en ellos. Igual que en el espacio $d$ , puede definirse una envolvente conexa de estos nodos-solución. Una función parabólica definida en los nodos estará necesariamente por fuera de esta envolvente conexa, y sólo la tocará en los propios nodos. Sin embargo, una condición necesaria para que la función objetivo tenga solución en un punto $x$ es que este punto esté dentro de la envolvente conexa. Como la función está fuera, la conclusión es que una función parabólica nunca puede recuperarse de esta manera; salvo en los propios nodos. Sin embargo, incluso en estos es de esperar que no se recupere una función parabólica, sino la propia envolvente.

Una manera alternativa de enfocar el problema es a partir de la propia forma de $\log Z$ . Para garantizar que la función tenga un mínimo, podemos examinar su límite cuando $\lambda$ y $\beta$ son muy grandes en valor absoluto.

Es fácil demostrar lo siguiente:

Límite $\lambda\rightarrow\infty$

En este límite, $\log Z \rightarrow \lambda (x-x_b)$ , donde $x_b$ es el punto más ... a $x$ por la derecha...

Límite $\lambda\rightarrow\infty$

En este límite, $\log Z \rightarrow \lambda (x-x_c)$ , donde $x_c$ es el punto más ... a $x$ por la derecha...

Límite $\beta\rightarrow -\infty$

En este límite, $\log Z \rightarrow - \beta (x-x_d)^2$ , donde $x_d$ es el punto más ... alejado...

Límite $\beta\rightarrow -\infty$

Este es el límite conflictivo, ya que $\log Z$ puede hacerse arbitrariamente pequeño.

En la figura 6.3 se muestra un ejemplo sencillo, para sólo dos puntos. La situación cualitativa no cambia si se añaden más, como se ha explicado, ni tampoco en dimensiones superiores.

Figura: Dibujo de la función $\log(1+\exp(-x - y)+\exp( x - y))$ .

Una manera de evitar esto es, sencillamente, añadir una pendiente a la función objetivo, que ``atraiga'' al mínimo del infinito. Esto se muestra en la figura 6.3.

Figura: Dibujo de la función $\log(1+\exp(-x - y)+\exp( x - y))+0.5y$ .

Al añadir esta pendiente, realmente estamos contemplando la siguiente minimización:

$$\min_{\lambda,\beta} \left( \beta g + \log \sum_a e^{\lambda (x-x_a)-\beta (x-x_a)^2} \right),$$

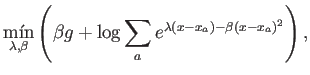
Otra manera de escribir esto mismo es:

$$\beta g + \log \sum_a e^{\lambda (x-x_a)-\beta (x-x_a)^2} = \log \sum_a e^{\lambda (x-x_a)-\beta \left[(x-x_a)^2 -g \right]} ,$$

lo que significa que nuestra ligadura original $L_2$ ha sido cambiada por esta otra:

$$L'_2=\beta \sum_a s_a \left[ (x-x_a)^2 - g \right].$$

Esta ligadura corresponde a imponer:

$$\sum_a s_a x_a^2 = x^2 + g .$$

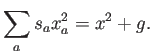
Es decir: una función cuadrática no puede reproducirse exactamente, pero una función cuadrática desplazada por una función $g(x)>0$ , sí podría. Por ello, esta función se denomina ``de salto'' (gap function). Este salto, corresponde, además, al desplazamiento vertical que habría que aplicarle a una parábola para meterla dentro de la envolvente conexa.

Una vez que este hecho se ha asimilado, se siguen una serie de conclusiones acerca de la forma general de la función $g(x)$ :

Las funciones base son

$$s_a=\frac{1}{Z}\exp(f_a),$$ (6.7)

donde

$$f_a=\lambda (x-x_a) -\beta ((x-x_a)^2-g)$$ (6.8)