Laplaciano SPH

Como se discute claramente en [5], a partir de la fórmula para la interpolación de una función en SPH,

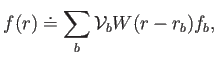
$\displaystyle f(r) \doteq \sum_b \mathcal{V}_b W(r-r_{b}) f_b,$

con el volumen SPH

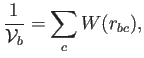
$\displaystyle \frac{1}{\mathcal{V}_b} = \sum_c W(r_{bc}) ,$

uno escribiría

$\displaystyle \nabla^2 f(r) \doteq \sum_b \mathcal{V}_b f_b \nabla^2 W(r-r_{b}).$

(5.4)

Sin embargo, esta expresión directa para el laplaciano presenta una serie de desventajas:

extrema sensibilidad a la regularidad de las posiciones de las partículas, un fenómeno claramente similar a lo que hemos visto arriba para elementos finitos.
el hecho de que $\nabla^2 W$ es una función que tiene valores negativos lleva a fenómenos sin sentido físico; por ejemplo en la ley de Fourier de la difusión del calor uno podría tener flujo de calor de partículas frías a otras calientes.

Por ello, se suele emplear esta expresión,

$\displaystyle \nabla^2 f(r) \doteq \sum_b \mathcal{V}_b (f_a-f_b) F(r-r_{b}),$

(5.5)

donde la función

está definida por

$\displaystyle \mathbf{r} F=\nabla W .$

Por ejemplo, para un kernel gaussiano $W=\exp(-\alpha r^2)$ , la función sería simplemente $F=-2\alpha W$ .

Esta expresión presenta un comportamiento típico en SPH: no converge si la resolución se mantiene constante; es decir, si el número de vecinos (en promedio) de cada partícula no cambia. Esto se consigue escalando la anchura de la función núcleo igual que la distancia media entre partículas. Si, por el contrario, la anchura se fija pero se incrementa el número de partículas, la expresión sí converge (a un coste computacional cada vez más elevado, claro está).

Daniel Duque 2011-11-10