Dos dimensiones
En dos dimensiones colocaremos 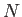 partículas sobre el cuadrado unidad
partículas sobre el cuadrado unidad
![$ [0,1]\times[0,1]$](img309.png) en estas posibles disposiciones:
en estas posibles disposiciones:
- Sobre una malla regular cuadrada, con las partículas en posiciones
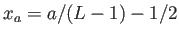 ,
, ![$ a\in[1,L]$](img311.png) , con
, con
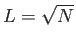 , y similarmente para
, y similarmente para
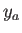 .
.
- Colocadas al azar, con componentes cartesianas tomadas de
números aleatorios entre 0
y
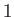 (éstos no incluidos).
(éstos no incluidos).
- Como estado intermedio, también contemplamos una perturbación de
la malla regular cuadrada, en la que cada partícula puede
desplazarse al azar dentro de un cuadrado cuyo lado es un
 de
la distancia entre partículas.
de
la distancia entre partículas.
- Por último, utilizamos el generador de mallas (``mallador'') de
la aplicación GiD [26], diseñado justamente para calcular
mallas que tengan buenas propiedades.
En este caso la función que utilizamos es
que cumple condiciones de Dirichlet homogéneas en
el cuadrado unidad y cuyo laplaciano exacto es
En la figura 5.7 se muestran 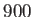 partículas colocadas
al azar sobre el cuadrado unidad. Se dibuja también la triangulación de
Delaunay correspondiente. Además se incluyen las ``partículas de frontera'',
necesarias a la hora de implementar las condiciones de contorno (en una
dimensión bastaba con dos, que situábamos en 0
y
partículas colocadas
al azar sobre el cuadrado unidad. Se dibuja también la triangulación de
Delaunay correspondiente. Además se incluyen las ``partículas de frontera'',
necesarias a la hora de implementar las condiciones de contorno (en una
dimensión bastaba con dos, que situábamos en 0
y 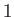 ). Estas partículas
reciben el valor 0
y se tienen en cuenta como vecinas de las partículas
interiores (los bordes de la triangulación de color rojo), aunque no se
calcula el laplaciano sobre ellas.
). Estas partículas
reciben el valor 0
y se tienen en cuenta como vecinas de las partículas
interiores (los bordes de la triangulación de color rojo), aunque no se
calcula el laplaciano sobre ellas.
Figura:
Partículas al azar sobre el
cuadrado unidad. Círculos azules sólidos: partículas originales;
círculos azules vacíos: partículas del borde añadidas. Segmentos
negros: bordes de Delaunay internos; segmentos rojos: bordes
externos.
|
|
Figura:
Aproximación de elementos finitos al
laplaciano en 2D (círculos azules), comparada con el laplaciano
exacto 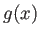 (asteriscos verdes) .
(asteriscos verdes) .
|
|
Igual que antes, calculamos el laplaciano mediante dos versiones: la
completa y la de masa acumulada. En la figura 5.8 se
muestra el resultado de la segunda versión para las posiciones
aleatorias de la figura 5.7. Evidentemente, el
resultado no es muy satisfactorio, con bastante dispersión cerca de
los extremos de la función.
Para cuantificar esta dispersión y su dependencia del número de puntos, de
nuevo utilizamos el error relativo 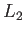 , ecuación
(5.3). Los resultados se muestran en la figura
5.9. Se puede concluir lo siguiente:
, ecuación
(5.3). Los resultados se muestran en la figura
5.9. Se puede concluir lo siguiente:
- El método de elementos finitos no es convergente en
disposiciones desordenadas (aleatorias o perturbadas), en ninguna de
las dos versiones.
- La aproximación de masa acumulada es, al contrario que en una
dimensión, mejor que la completa.
- En mallas ordenadas el método sí converge. El ajuste revela que
la convergencia es de orden
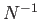 , más lenta que en una
dimensión. Esta convergencia es muy sensible al orden de la
disposición de partículas: sólo se dibujan los resultados para
, más lenta que en una
dimensión. Esta convergencia es muy sensible al orden de la
disposición de partículas: sólo se dibujan los resultados para 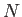 que son cuadrados perfectos; en otros casos, los errores son
superiores debido a la imposibilidad de crear una malla cuadrada
perfecta.
que son cuadrados perfectos; en otros casos, los errores son
superiores debido a la imposibilidad de crear una malla cuadrada
perfecta.
- El método también converge en mallas de buena calidad generadas
por el programa especializado GiD. En este segundo caso, una
visualización de la malla (figura 5.10) permite
comprobar que se trata de una malla regular triangular, salvo en
ciertas ``costuras'' diagonales. La presencia de estas costuras
empeora la convergencia, pero su importancia disminuye al crecer
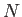 .
.
Figura 5.9:
Convergencia del laplaciano
aproximado por el método FEM en 2D. Círculos azules: versión
completa en disposición aleatoria; diamantes azules: versión
completa en disposición regular; triángulos azules: versión completa
en disposición cuadrada perturbada; cuadrados rojos: versión de masa
acumulada en disposición aleatoria; cruces rojas: versión de masa
acumulada en disposición regular; aspas rojas: versión de masa
acumulada en disposición cuadrada perturbada. Línea azul continua:
ajuste a una ley de potencia de exponente 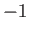 ; línea azul punteada:
ajuste a una ley de potencia genérica (el exponente resulta ser de
; línea azul punteada:
ajuste a una ley de potencia genérica (el exponente resulta ser de
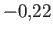 ).
).
|
|
Figura:
Partículas sobre el
cuadrado unidad generadas mediante el programa GiD. Símbolos como en
figura 5.7.
|
|
Daniel Duque
2011-11-10
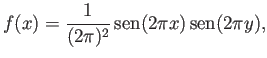
![]() partículas colocadas
al azar sobre el cuadrado unidad. Se dibuja también la triangulación de
Delaunay correspondiente. Además se incluyen las ``partículas de frontera'',
necesarias a la hora de implementar las condiciones de contorno (en una
dimensión bastaba con dos, que situábamos en 0
y
partículas colocadas
al azar sobre el cuadrado unidad. Se dibuja también la triangulación de
Delaunay correspondiente. Además se incluyen las ``partículas de frontera'',
necesarias a la hora de implementar las condiciones de contorno (en una
dimensión bastaba con dos, que situábamos en 0
y ![]() ). Estas partículas
reciben el valor 0
y se tienen en cuenta como vecinas de las partículas
interiores (los bordes de la triangulación de color rojo), aunque no se
calcula el laplaciano sobre ellas.
). Estas partículas
reciben el valor 0
y se tienen en cuenta como vecinas de las partículas
interiores (los bordes de la triangulación de color rojo), aunque no se
calcula el laplaciano sobre ellas.
![\includegraphics[width=0.5\textwidth]{points_rand_900}](img318.png)
![\includegraphics[width=0.8\textwidth]{sinsin_900}](img319.png)
![]() , ecuación
(5.3). Los resultados se muestran en la figura
5.9. Se puede concluir lo siguiente:
, ecuación
(5.3). Los resultados se muestran en la figura
5.9. Se puede concluir lo siguiente:
![\includegraphics[width=0.5\textwidth]{fem_lapl_2d_l2}](img322.png)
![\includegraphics[width=0.5\textwidth]{points_gid_1000}](img324.png)