Fuerzas de superficie

Estas fuerzas operan sobre una partícula de fluido por contacto; salvo en la frontera del fluido, este contacto es con partículas circundantes. Si tomamos una partícula cúbica de volumen $\mathcal{V}=dx\, dy\, dz$ , la fuerza neta en la dirección $x$ será en general debida a esfuerzos, o tensiones (stresses) sobre cada una de las seis caras del cubo. Estos esfuerzos se consideran positivos si se ejercen hacia fuera de la partícula (en el sentido del vector normal a la superficie, según el convenio habitual).

Si tomamos tres caras del cubo perpendiculares y con áreas $dy dz$ , $dx dy$ y $dx dz$ la fuerza de contacto sobre la partícula a través de estas caras será:

$$dF_{x,\mathrm{tres\ caras}}= \tau_{xx} dy dz + \tau_{xy} dx dz + \tau_{xz} dx dy ,$$ (2.6)

donde $\tau_{ij}$ son los esfuerzos correspondientes.

Como existen otras tres caras paralelas, la fuerza neta sobre el cubo en la dirección $x$ resulta estar relacionada con el cambio de los esfuerzos en sus direcciones correspondientes. Por ejemplo

$$d \tau_{xx} \approx \frac{\partial \tau_{xx}}{\partial x} dx.$$

Así pues,

$$dF_{x,\mathrm{neta}}= \left( \frac{\partial \tau_{xx}}{\partial x... ...right) dx dz + \left( \frac{\partial \tau_{xz}}{\partial z} dz \right) dx dy$$

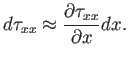
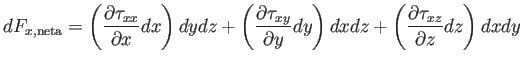
Así pues, la fuerza por unidad de volumen será

$$f_x= \frac{dF_{x,\mathrm{neta}}}{\mathcal{V}}= \frac{\partial \ta... ...\frac{\partial \tau_{xy}}{\partial y} + \frac{\partial \tau_{xz}}{\partial z}.$$

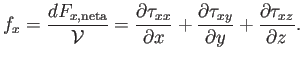
Para tener en cuenta las otras componentes de $f$ , se puede definir un tensor de esfuerzos $\tau$ que, como el tensor de deformaciones $\epsilon$ es también de orden dos y simétrico. La conexión con las fuerzas de superficie es, en general

$$f=\nabla \cdot \tau ;$$

en coordenadas cartesianas,

$$f_i=\frac{\partial \tau_{ij}}{\partial x_j} .$$

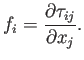
El caso anterior corresponde a $i=1$ .

La ecuación del momento es, por tanto:

$$\rho \frac{d v}{d t} = \rho g +\nabla\cdot \tau .$$ (2.7)

Para cerrar esta ecuación hace falta encontrar una expresión de los esfuerzos en función de la velocidad, lo cual por lo general supone conectar de algún modo el tensor de esfuerzos, $\tau$ , con el de deformaciones, $\epsilon$ .