4.2. Cálculo aproximado de integrales con sumas de Riemann#

4.2.1. Introducción: planteamiento del problema#

Calcular la integral de Riemann (o integral definida)

\[ \intop_{a}^{b}f(x)dx \]

es en general difícil. Por eso resulta útil disponer de métodos para calcular el valor de la integral de modo aproximado.

4.2.2. Sumas de Riemann#

El método más sencillo es aproximar la integral por sumas de Riemann. Se divide el intervalo \((a,b)\) en \(N\) subintervalos

\[ (x_{0},x_{1}),(x_{1},x_{2}),(x_{2},x_{3}),\ldots(x_{N-1},x_{N}). \]

de igual longitud

\[ h=\frac{b-a}{N}. \]

Los extremos de los subintervalos se calculan como

\[ x_{n}=a+n\cdot h,\ \ \ n=0,1,2,\ldots,N. \]

A continuación se escoge un punto en cada subintervalo

\[ \xi_{n}\in(x_{n},x_{n+1}),\ \ \ n=0,1,2,\ldots,N-1 \]

y se aproxima

\[ \intop_{x_{n}}^{x_{n+1}}f(x)dx\sim hf(\xi_{n}). \]

Esto significa que el área bajo el gráfico de \(f\) en el intervalo \((x_{n},x_{n+1})\) se aproxima por el área del rectángulo de base \(x_{n+1}-x_{n}=h\) y altura \(f(\xi_{n})\).

Sumando resulta finalmente

\[ \intop_{a}^{b}f(x)dx\sim\sum_{n=0}^{N-1}hf(\xi_{n})=h\sum_{n=0}^{N-1}f(\xi_{n}). \]

Esta suma recibe el nombre de suma de Riemann.

Los puntos intermedios \(\xi_{n}\in(x_{n},x_{n+1})\) pueden escogerse de muchos modos, pero en general la elección no influye en el resultado cuando \(N\) es grande. Por eso suelen tomarse valores de \(\xi_{n}\) que se calculan fácilmente.

Las elecciones más frecuentes son:

  • \(\xi_{n}\) es el extremo izquierdo del subintervalo \((x_{n},x_{n+1})\)

\[ \xi_{n}=x_{n}=a+n\cdot h, \]

de donde resulta

\[ \intop_{a}^{b}f(x)dx\sim h\sum_{n=0}^{N-1}f(a+n\cdot h). \]

  • \(\xi_{n}\) es el extremo derecho del subintervalo \((x_{n},x_{n+1})\)

\[ \xi_{n}=x_{n+1}=a+(n+1)\cdot h, \]

de donde resulta

\[ \intop_{a}^{b}f(x)dx\sim h\sum_{n=0}^{N-1}f(a+(n+1)\cdot h). \]

  • \(\xi_{n}\) es el punto medio del subintervalo \((x_{n},x_{n+1})\)

\[ \xi_{n}=\frac{x_{n}+x_{n+1}}{2}=a+(n+\frac{1}{2})\cdot h, \]

de donde resulta

\[ \intop_{a}^{b}f(x)dx\sim h\sum_{n=0}^{N-1}f(a+(n+\frac{1}{2})\cdot h). \]
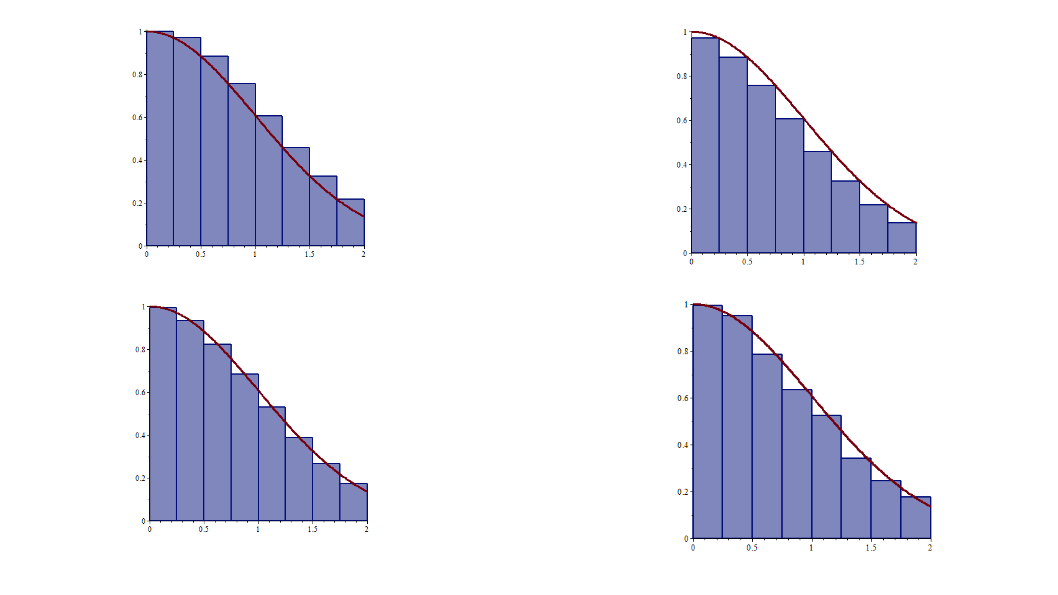
_images/riem.png

Arriba a la izquierda, aproximación con las sumas de Riemann eligiendo el extremo izquierda, arriba a la derecha, aproximación con el extremo derecho, abajo a la izquierda, se ha elegido el punto medio y abajo a la derecha se ha elgido un punto arbitrario.

Ejercicio

  1. Sumas de Riemann para la integral \(\intop_{0}^{2}e^{-\frac{x^{2}}{2}}dx\) para \(N=8\) y extremos izquierdos, extremos derechos, puntos medios y puntos aleatorios

4.2.3. Método del trapecio#

Este método suele ser más preciso para aproximar el valor de la integral. Esto significa que se requiere \(N\) más pequeño para obtener una buena aproximación. En cada subintervalo se aproxima el área bajo la curva por el área del trapecio inscrito, resulta la fórmula

\[ \int_{a}^{b}f(x)dx\sim \sum_{n=1}^{N}\left(\frac{f(a+(n-1)h) + f(a+nh)}{2} \right)h = h\left(\frac{f(a)+f(b)}{2}+\sum_{n=1}^{N-1}f(a+n\cdot h)\right) \]

4.2.4. Ejercicios#

  1. Definir la función riemann_izq(f,a,b,N) que devuelve el valor de la suma de Riemann de la integral

\[ \intop_{a}^{b}f(x)dx \]

con \(N\) subintervalos y los extremos izquierdos como puntos intermedios.

  1. Definir la función riemann_der(f,a,b,N) que devuelve el valor de la suma de Riemann de la integral

\[ \intop_{a}^{b}f(x)dx \]

con \(N\) subintervalos y los extremos derechos como puntos intermedios.

  1. Definir la función trapecio(f,a,b,N) que devuelve el valor de la suma de Riemann de la integral

\[ \intop_{a}^{b}f(x)dx \]

con \(N\) subintervalos.

  1. Teniendo en cuenta que

\[ \intop_{0}^{1}x^{3}dx=\frac{1}{4}, \]

calcular el error que se obtiene al aproximar esta integral usando las funciones riemann_izq, riemann_der y trapecio(f,a,b,N) con \(N=1000\).

  1. Escogemos \(f(x)=1\), y definimos la función F(x)=riemann_izq(f,0,x,1000), es decir

def F(x):
    return riemann_izq(f,0,x,1000)

Representar gráficamente la función \(F(x)\) en \((0,5).\) ¿Qué función se ha obtenido? ¿Qué significa este resultado?

  1. Repetir el ejercicio anterior para \(g(x)=\cos(x)\).

  1. Implementar la siguiente aproximación de la regla del trapecio de la integral definida de \(f(x)\) en el intervalo \((a,b)\) cuando \(h=(b-a)/N.\)

\[ \int_{a}^{b}f(x)dx\sim \sum_{n=1}^{N}\left(\frac{f(a+(n-1)h) + f(a+nh)}{2}\right)h = h\left(\frac{f(a) + f(b)}{2} +\sum_{n=1}^{N-1}f(a+nh) \right) \]

Escribir la función regla_trapecio(f, a, b, N) donde f es una función matemática definida como función de Python con def, \(a\) y \(b\) son los extremos del intervalo de integración y \(N\) es el número de subintervalos de la correspondiente suma de Riemann. La función devuelve un número decimal con tres decimales.