3.3. Módulos#

Estrucutura modular
Cargar módulos
Ejemplo de módulos del usuario
Algunos módulos oficiales
Representación de funciones con matplotlib y numpy
Ejercicios

3.3.1. Estructura modular#

El problema:

es muy complicado manejar todas las lineas de código necesarias para problemas complejos
reutilización de código que debe ser usado por otros programas

Una solución

las funciones permiten reutilizar un pedazo de código que resuelve un problema de una formasimple
todas las funciones necesarias para reolver un tipo de problemas se encapsulan en un módulo

Un módulo es un fichero .py que contiene funciones, comandos del lenguaje de programación; en general, expresiones del lenguaje de progarmación que se suelen usar para resolver un clase de problemas similares.

Hay módulos predefinidos

módulos que contienen las definiciones de funciones matemáticas (math)
módulos que reunen las funciones y comandos necesarios para hacer análisis estadísticos (scipy)
módulos que contienen las funciones necesarias para representaciónes de datos, funciones matemáticas (matplotlib)
…

Pero los usuarios también pueden definir sus propios módulos. Estos deben guardarse en la misma carpeta donde se encuentra el cuaderno de Jupyter donde se van a utilizar.

3.3.2. Cargar módulos#

Antes de utilizar un módulo debemos cargarlo. Hay tres formas de hacerlo (supongamos que el módulo se llama mi_modulo):

import mi_modulo: las funciones definidas en el fichero mi_modulo.py se invocan con el prefijo mi_modulo.
- Para utilizar la función funcion1(x) del módulo mi_modulo se escribir mi_modulo.funcion1(x)
import mi_modulo as mm: las funciones se invocan con el prefijo mm: mm.funcion1(x)
- Para utilizar la función funcion1(x) del módulo mi_modulo se escribir mm.funcion1(x)
from mi_modulo import *: las funciones se invocan sin prefijo, directamente con su nombre

3.3.3. Ejemplo de módulo del usuario#

Hemos creado, a modo de ejemplo, un módulo con algunas funciones para calcular valores relacionados con la circunferencia. Están guardadas en un fichero llamado circulo.py. En este caso, las tres formas de cargar en la memoria de la máquina el módulo circulo para tener accesibles las funciones definidas en el fichero circulo.py ( este fichero debe estar en la misma carpeta que contiene este cuaderno ) serían:

import circulo: las funciones definidas en el fichero circulo.py se invocan con el prefijo circulo.
import circulo as c: las funciones se invocan con el prefijo c.
from circulo import *: las funciones se invocan sin prefijo, directamente con su nombre

import circulo
pi = 3
print(pi)
print(circulo.pi)
print(circulo.area(3))
print(circulo.circunferencia(3))

3
14159
27431
849539999999998

import circulo as c
print(c.pi)
print(c.area(3))

3.14159
28.27431

from circulo import *
print(pi)
print(area(3))

3.14159
28.27431

3.3.4. Algunos módulos ‘’oficiales’’#

string https://docs.python.org/2/library/string.html
keyword https://docs.python.org/2/library/keyword.html
math https://docs.python.org/3/library/math.html
scipy: https://www.scipy.org/
matplolib.pyplot https://matplotlib.org/
numpy https://numpy.org/
sympy https://www.sympy.org/en/index.html
random https://docs.python.org/3/library/random.html

Módulos stringy keyword

import string
import keyword

string.ascii_letters

'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ'

string.ascii_lowercase

'abcdefghijklmnopqrstuvwxyz'

string.punctuation

'!"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~'

string.printable

'0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~ \t\n\r\x0b\x0c'

keyword.kwlist

['False',
 'None',
 'True',
 'and',
 'as',
 'assert',
 'async',
 'await',
 'break',
 'class',
 'continue',
 'def',
 'del',
 'elif',
 'else',
 'except',
 'finally',
 'for',
 'from',
 'global',
 'if',
 'import',
 'in',
 'is',
 'lambda',
 'nonlocal',
 'not',
 'or',
 'pass',
 'raise',
 'return',
 'try',
 'while',
 'with',
 'yield']

Módulo math

El módulo math contiene funciones matemáticas: \(\sin(x)\), \(\cos(x)\), \(\log(x)\), \(\exp(x)= e^x\), \(\pi\), etc.

import math as m

m.sin(18)

-0.750987246771676

help()

Welcome to Python 3.8's help utility!

If this is your first time using Python, you should definitely check out
the tutorial on the Internet at https://docs.python.org/3.8/tutorial/.

Enter the name of any module, keyword, or topic to get help on writing
Python programs and using Python modules.  To quit this help utility and
return to the interpreter, just type "quit".

To get a list of available modules, keywords, symbols, or topics, type
"modules", "keywords", "symbols", or "topics".  Each module also comes
with a one-line summary of what it does; to list the modules whose name
or summary contain a given string such as "spam", type "modules spam".

---------------------------------------------------------------------------
StdinNotImplementedError                  Traceback (most recent call last)
Input In [12], in <cell line: 1>()
----> 1 help()

File /usr/lib/python3.8/_sitebuiltins.py:103, in _Helper.__call__(self, *args, **kwds)
    101 def __call__(self, *args, **kwds):
    102     import pydoc
--> 103     return pydoc.help(*args, **kwds)

File /usr/lib/python3.8/pydoc.py:1918, in Helper.__call__(self, request)
   1916         else:
   1917             self.intro()
-> 1918             self.interact()
   1919             self.output.write('''
   1920 You are now leaving help and returning to the Python interpreter.
   1921 If you want to ask for help on a particular object directly from the
   1922 interpreter, you can type "help(object)".  Executing "help('string')"
   1923 has the same effect as typing a particular string at the help> prompt.
   1924 ''')

File /usr/lib/python3.8/pydoc.py:1930, in Helper.interact(self)
   1928 while True:
   1929     try:
-> 1930         request = self.getline('help> ')
   1931         if not request: break
   1932     except (KeyboardInterrupt, EOFError):

File /usr/lib/python3.8/pydoc.py:1950, in Helper.getline(self, prompt)
   1948 """Read one line, using input() when appropriate."""
   1949 if self.input is sys.stdin:
-> 1950     return input(prompt)
   1951 else:
   1952     self.output.write(prompt)

File /usr/local/lib/python3.8/dist-packages/ipykernel/kernelbase.py:1174, in Kernel.raw_input(self, prompt)
   1167 """Forward raw_input to frontends
   1168 
   1169 Raises
   1170 ------
   1171 StdinNotImplementedError if active frontend doesn't support stdin.
   1172 """
   1173 if not self._allow_stdin:
-> 1174     raise StdinNotImplementedError(
   1175         "raw_input was called, but this frontend does not support input requests."
   1176     )
   1177 return self._input_request(
   1178     str(prompt),
   1179     self._parent_ident["shell"],
   1180     self.get_parent("shell"),
   1181     password=False,
   1182 )

StdinNotImplementedError: raw_input was called, but this frontend does not support input requests.

m.log2(2)

1.0

m.log(10)

2.302585092994046

m.log(m.exp(1))

1.0

m.acos(-1)

3.141592653589793

m.cos(m.pi)

-1.0

Módulo random

import random as rm

n = rm.randint(1,6)

cont_1 = 0
cont_2 = 0
cont_3 = 0
cont_4 = 0
cont_5 = 0
cont_6 = 0
for m in range(600000):
    u = rm.randint(1,6)
    if u == 1:
        cont_1 += 1
    if u == 2:
        cont_2 += 1
    if u == 3:
        cont_3 += 1
    if u == 4:
        cont_4 += 1
    if u == 5:
        cont_5 += 1
    if u == 6:
        cont_6 += 1
        
print(1, '-->', cont_1)
print(2, '-->', cont_2)
print(3, '-->', cont_3)
print(4, '-->', cont_4)
print(5, '-->', cont_5)
print(6, '-->', cont_6)

--> 100728
--> 99829
--> 99920
--> 99465
--> 100245
--> 99813

3.3.5. Representación de funciones con `matplotlib` y `numpy`#

Referencia:

https://matplotlib.org/stable/users/index.html

https://numpy.org/doc/stable/reference/?v=20221104163338

Funciones de una variable con valores reales

A continuación tenemos un ejemplo con la representación de una función de una variable con valores reales sin usar numpy. Es habitual importar el submodulo que necesitamos para hacer las gráficas con el alias plt.

Para representar funciones, se representan puntos de la gráfica de la funicón en cuestión. Estos punto se unen por defento con segmentos. Cuantos más puntos dibujemos, la representación obtenida más parecerá una línea “lisa”.

import matplotlib.pyplot as plt

En el caso de abajo solo tenemos un número reducido de puntos de la gráfica de la función.

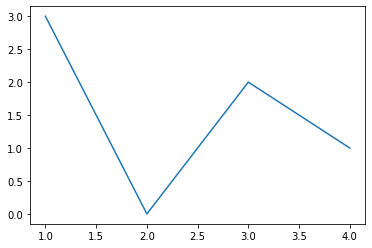
Abajo dibujamos la gráfica de la funicón que pasa por los puntos

\[ (1,3), \quad (2,0),\quad (3,2), \quad (4,1) \]

Por lo tanto, los valores de las \(x\)’s son [1,2,3,4] y los de las \(y\)’s son [3,0,2,1]. Por defecto, se dibujan segmentos que van uniendo los sucesivos puntos de la gráfica:

X1 = [1,2,3,4]
Y1 = [3,0,2,1]

plt.plot(X1, Y1)
plt.show()

Ahora dibujamos solo los puntos. Observad el parámetro opcional que se usa.

plt.plot(X1, Y1, 'o')
plt.show()

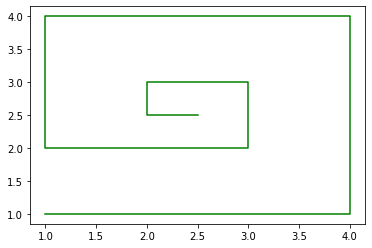
Podemos dibujar puntos de forma que al unirlos con segmentos no resulte la gráfica de una función:

U1 = [1,4,4,1,1,3,3,2,2,2.5]
V1 = [1,1,4,4,2,2,3,3,2.5,2.5]
plt.plot(U1,V1, 'g-')
plt.show()

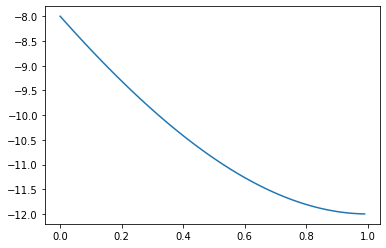
Ahora utilizamos muchos puntos para que al unirlos con segmentos no perezca una poligonal

X2 = [0 + 0.01*n for n in range(100)]
Y2 = [x**3 + 2*x**2 - 7*x - 8 for x in X2]
plt.plot(X2, Y2)
plt.show()

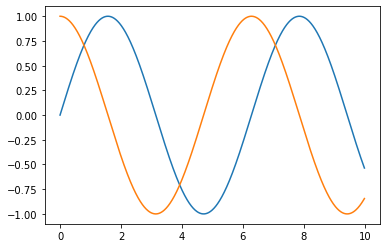
Ahora dos funciones en la misma gráfica. Importamos el módulo math

import math as m

X3 = [0 + 0.01*n for n in range(1000)]
Y3_1 = [m.sin(x) for x in X3]
Y3_2 = [m.cos(x) for x in X3]

plt.plot(X3, Y3_1)
plt.plot(X3, Y3_2)

plt.show()

Algunas opciones interesantes de este módulo:

título
legenda
ejes
grosor
tipo de trazo
color

plt.plot(X3, Y3_1, '--', label = 'seno', linewidth = 4, color = 'g')
plt.plot(X3, Y3_2, label = 'coseno', color = 'b')

plt.xlabel('Eje X')
plt.ylabel('Eje Y')
plt.title('Funciones circulares')
plt.legend()

plt.show()

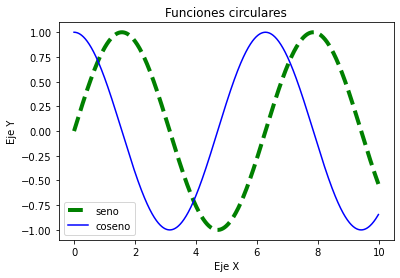
Algunos valores para el tipo de trazo y el color:

tipo de trazo: '-', '--', ':', '-.', 'o', '+'
color: 'r', 'g', 'b', 'y','c', 'm', 'y', 'k'

Con el módulo numpy

Con el módulo numpy podemos facilitar el trabajo. Este módulo se suele importar con el alias np.

import numpy as np

X_4 = np.linspace(0, 10, 100)

plt.plot(X_4, np.sin(X_4), '--', label = 'seno', linewidth = 4, color = 'g')
plt.plot(X_4, np.cos(X_4), label = 'coseno', color = 'b')

plt.xlabel('Eje X')
plt.ylabel('Eje Y')
plt.title('Funciones circulares (con numpy)')
plt.legend()

plt.show()

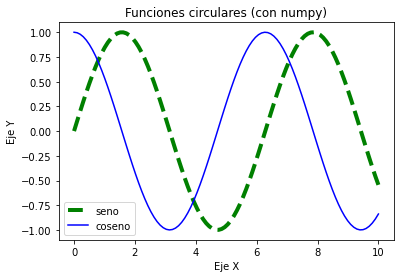
Funciones paramétricas

Cuando una función está definida de forma paramétrica procedemos de modo muy parecido.

Si tenemos la función \(x(t) = \cos(t)\), \(y(t)= \sin(t)\), el siguiente código dibuja su gráfico en el plano XY cuando \(t\) varía en el intervalo \((0,2\pi)\):

T = np.linspace(0, 2*np.pi, 200)

plt.plot(np.cos(T), np.sin(T))
plt.show()

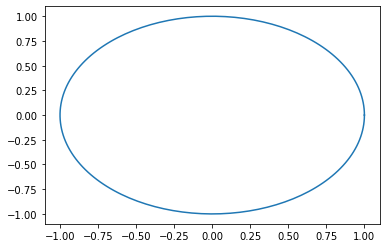
Aquí se podría utilizar las opciones antes indicadas para enriquecer esta figura ¿Cómo se podría conseguir que esta circunferncia no pareciera una elipse?

Consideraciones generales

Las ilustarciones o las figuras con gráficas de funciones nos sirven para visualizar datos. Para hacer este trabajo con matplotlib hemos de considerar tres niveles que constituyen tres objetos de Python diferentes.

El primer nivel es el de la figura (Figure). Esto es el contenedor de la ilustración que vamos a generar.
El segundo nivel son los ejes (Axes). Para dibujar datos (puntos) necesitamos ejes. Si los puntos tienen dos coordenadas solo necesitaremos dos ejes; si los puntos tienen tres coordenadas necesitaremos tres ejes. Cada figura puede tener uno juego de ejes, varios juegos de ejes o ningún juego de ejes. Pero los ejes siempre deben estar contenidos en una figura.
El tercer nivel es la gráfica (Plot). Cada juego de ejes puede contener una gráfica, varias gráficas o ninguna gráfica. Sin embargo, toda gráfica debe tener unos ejes que estarán contenidos en una figura.

Para crear una figura no es necesario crear explíctamente los tres objetos, los tres niveles. Hay comandos que generan las tres cosas a la vez. Es decir, la gráfica, los ejes para representarla y la figura que contiene todo. Como en los ejemplos que hemos visto hasta ahora. También hay comandos que generan los ejes y la figura; después se generan las gráficas con otros comandos.

Veamos un ejemplo con la anterior gráfica.

# Se genera una figura y se almacena en la variable 'fig4' 
fig4 = plt.figure(figsize = (5,5))

# El título de la figura
fig4.suptitle('Circunferencia')

# Creamos, simultáneamente el primer juego de ejes y la gráfica del primer juego de ejes
T = np.linspace(0, 2*np.pi, 200)
plt.plot(np.cos(T), np.sin(T), label= 'Circunferencia $x^2+y^2=1$')
plt.legend()

# Etiquetas para los ejes de la primera fugura
plt.xlabel('x')
plt.ylabel('y')

plt.show()

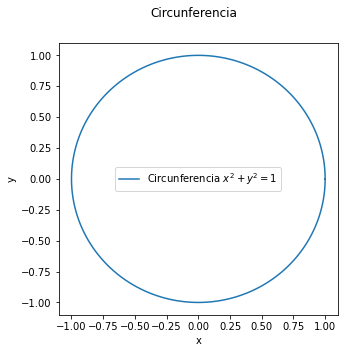
Se ha creado un marco cuadrado para que se visualice la circunferncia adecuadamente. Esto se ha hecho con la siguiente línea:

fig4 = plt.figure(figsize = (5,5))

Figura simple con gráficas de funciones de una variable en ejes distintos

# Se genera una figura y se almacena en la variable 'fig4' 
fig4 = plt.figure('La cuarta')

# El título de la figura
fig4.suptitle('Parábola y cúbica')

# Creamos el primer juego de ejes. Habrá dos en fila.
plt.subplot(121, title = 'Parábola')

# Generamos los valores de las x's
x = np.linspace(-5, 5, 20)

# La gráfica del primer juego de ejes
plt.plot(x, x**2, label= 'Parábola $y=x^2$')
plt.legend()

# Etiquetas para los ejes de la primera fugura
plt.xlabel('x')
plt.ylabel('y')

# El segundo juego de ejes
plt.subplot(122, title = 'Cúbica')

# La gráfica del segundo juego de ejes
plt.plot(x, x**3, label= 'Cúbica $y=x^3$')            
plt.legend()   

# Etiquetas para los ejes de la segunda figura. Quitamos la 'y' para que no se solape
plt.xlabel('x')
# plt.ylabel('y')


plt.show()

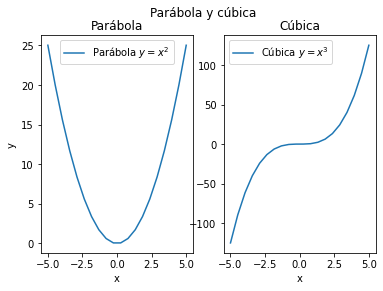
El comando \(\texttt{subplot}\) hace un trabajo similar a \(\texttt{plot}\) ya que crea la figura y los ejes automáticamente. Ahora crea una figura donde caben dos ejes colocados en una sola fila con dos columnas. Este es el significado de los dos primeros dígitos. El tercero informa de cuál de dos posibles ejes estamos considerando. Obsérvese como se situa el título de cada uno de los dos juegos de ejes y como se pone un título a la figura.

3.3.6. Ejercicios#

Dibujar los gráficos de las siguientes funciones en los intervalos que se indican:

a) \(f(x)= x^2-3x+1\) en \((0,5)\) utilizando 100 puntos.

b) \(f(x) = \cos(2x-3)\) en \((-\pi,\pi)\).
Dibujar en un mismo gráfico las funciones que se indican en cada apartado. Añade una leyenda que permita saber a qué función corresponde cada gráfico.

a) \(f(x)= \sqrt(x)\) y \(g(x) = x^2\) en \((0,2)\).

b) \(f_k(x) = x^k\) para \(k=1,2,3,4,5\) en \((-1,1)\).

c) \(f(x)=x^2e^{-x^2}\) y \(g(x)=x^4e^{-x^2}\) en \((0,4)\).
Dibujar los gráficos de las siguientes curvas paramétricas:

a) \(x(t)= \frac{1}{t}\sin(t)\), \(y(t)= \cos^2(t)\) para \(t \in (0,\pi]\).

b) \(x(t)= \cos(t^2)\), \(y(t)= t^3-t^2\) para \(t \in [0,8]\).

Cálculo Numérico y Programación

Módulos

Contents

3.3. Módulos#

3.3.1. Estructura modular#

3.3.2. Cargar módulos#

3.3.3. Ejemplo de módulo del usuario#

3.3.4. Algunos módulos ‘’oficiales’’#

3.3.5. Representación de funciones con `matplotlib` y `numpy`#

3.3.6. Ejercicios#

Cálculo Numérico y Programación

Módulos

Contents

3.3. Módulos#

3.3.1. Estructura modular#

3.3.2. Cargar módulos#

3.3.3. Ejemplo de módulo del usuario#

3.3.4. Algunos módulos ‘’oficiales’’#

3.3.5. Representación de funciones con matplotlib y numpy#

3.3.6. Ejercicios#

3.3.5. Representación de funciones con `matplotlib` y `numpy`#